Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 9.Problemas - Ex. 117
Uma usina de potência com turbina a gás opera em um ciclo Brayton ideal com regeneração () usando ar como fluido de trabalho. O ar entra no compressor a , e na turbina, a . Calor é transferido para o ar por meio de uma fonte externa a uma taxa de . Determine a potência produzida por essa usina (a) considerando calores específicos constantes à temperatura ambiente e (b) considerando a variação de calores específicos com a temperatura.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Bom... Para esboçar o nosso ciclo em um diagrama , temos que saber primeiramente se os processos de compressão e expansão serão totalmente isentrópicos ou não.
No caso os processos são totalmente isentrópicos.
O exercício nos disse que a pressão na entrada do compressor é de e na entrada da turbina é de . Para o ciclo com regeneração, teremos que:
Ou seja:
Como o ar entra no compressor a e na turbina a , temos que:
O ciclo Brayton real com regeneração é dado por:
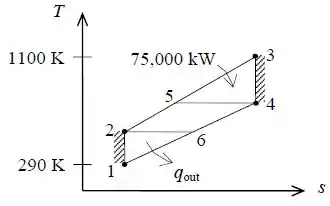
Passo 2
Agora vamos analisar os processos:
O processo é uma compressão isentrópica, logo:
Temos que:
Logo:
Substituindo os valores temos que:
Passo 3
Para a expansão , temos que:
Como:
Substituindo os valores, temos que:
Passo 4
Como a efetividade do regenerador é de , temos que:
E:
A eficiência térmica será:
Desenvolvendo, temos que:
Substituindo os valores, temos que:
Passo 5
Podemos então encontrar a potência do ciclo:
A potência será:
Passo 6
Para o item “b”, devemos encontrar a potência do ciclo, agora considerando calores específicos variáveis com a temperatura.
Ou seja, a partir das temperaturas fornecidas, teremos que encontrar na tabela suas respectivas propriedades de entalpia e pressão relativa para calcular as propriedades dos outros estados desconhecidos.
Temos que:
E:
Portanto, sabendo que:
E:
Temos que:
E:
Passo 7
A partir dos valores encontrados no passo anterior, podemos interpolar com o auxilio da tabela, suas respectivas entalpias correspondentes:
E:
Como a efetividade do regenerador é de , temos que:
E:
A eficiência térmica será:
Desenvolvendo, temos que:
Substituindo os valores, temos que:
Passo 8
Podemos então encontrar a potência do ciclo:
A potência será: