Enunciado
Termodinâmica - Van Wylen- Ed: 6º - Capítulo 7.Problemas - Ex. 17
Os refrigeradores de absorção, utilizados nas regiões onde não existe a distribuição de energia elétrica, operam a partir da queima de um combustível. Faça o esquema de um refrigerador de absorção utilizando dois ciclos térmicos e relacione a taxa de transferência de calor no espaço refrigerado com a taxa de transferência de calor dos gases de combustão. Como a relação obtida se comporta com as variações de temperatura dos gases de combustão de espaço refrigerado.
Passo 1
Fala galera, beleza? Bora resolver mais uma comigo?
Galera temos que montar um esquema de dois ciclos térmicos e determinar a equação que refere-se à relação da transferência de calor no reservatório de baixa temperatura com a taxa de calor fornecida pelo combustível.
Vamos partir
com o esquema em mãos:
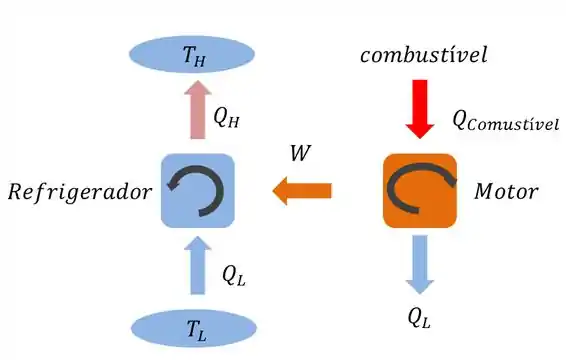
O motor recebe a explosão, efetua trabalho e o refrigerador faz o processo contrário do motor e libera .
Passo 2
Vamos assumir que o trabalho da máquina seja de eficiência da máquina de Carnot.
Utilizando a fórmula de uma máquina térmica real, para o motor, temos:
Isolando o trabalho:
Como o coeficiente de eficiência é definido por:
Substituindo na fórmula do trabalho:
Passo 3
Agora temos que relacionar o trabalho do motor com o trabalho do refrigerador.
Para o refrigerador, vamos utilizar os mesmos passos:
Utilizando a equação para um refrigerador real:
Isolando o trabalho:
Como o coeficiente de eficiência é definido por:
Substituindo na fórmula do trabalho:
Passo 4
Com o trabalho de cada máquina explicitado, podemos igualar as duas equações e resolver para .
Tendo uma nota que está modelagem é otimista, pois, tivemos que assumir que a eficiência do nosso motor e refrigerador sejam iguais a máquina de Carnot.
É isso galera, valeu!