Enunciado
Termodinâmica - Sonntag, R.E. e Borgnakke, C. -Fundamentos da Termodinâmica- Ed: 1º - Capítulo 6.Problemas - Ex. 73
Um tanque de , mostrado na Fig.P6.73, inicialmente evacuado, está conectado através de uma válvula a uma linha de fornecimento de ar a e . A válvula é aberta e o ar escoa para dentro do tanque até que a pressão atinge . Determine a temperatura final e a massa no interior do tanque, admitindo que o processo é adiabático. Desenvolva uma expressão para a relação entre a temperatura do ar na linha e a temperatura final do tanque usando calores específicos constantes.
Passo 1
Fala pessoal, tudo tranks? Mais uma aí pra conta!
Bora lá! Considerando o tanque como volume de controle...
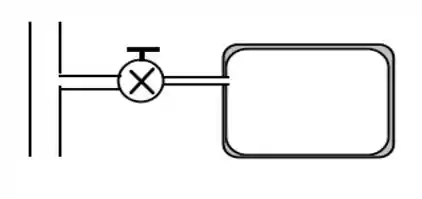
E com isso, baseado na equação de energia, ficamos com...
Passo 2
Assim, com base na tabela abaixo do vapor saturado, ficamos com o seguinte valor de energia interna...
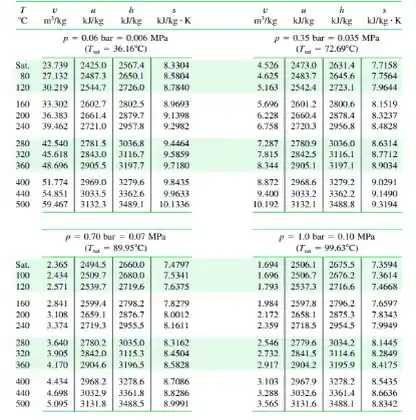
Onde;
Assim, com base na equação dos gases...
Podemos encontrar a massa correspondente nesses estado...
Passo 3
Em seguida, vamos tratar de achar a equação que o problema pediu para a relação entre a temperatura do ar na linha e a temperatura final do tanque usando calores específicos constantes...
Dado que...
Dessa forma, podemos fazer a relação...
Onde, com base na relação dos gases...
Uma vez que...
E é constante...