Enunciado
Termodinâmica - Sonntag, R.E. e Borgnakke, C. -Fundamentos da Termodinâmica- Ed: 1º - Capítulo 11.Problemas - Ex. 31
Um suprimento permanente de de vapor d’água saturado a é requerido para a secagem de polpa de madeira em uma usina de papel (veja Fig. P11.31). Decidiu-se que o fornecimento do vapor deve ser por co-geração, isto é, ele será suprido pela descarga de uma turbina a vapor. Água a e é bombeada a para alimentar um gerador de vapor, cuja saída é a . Qual é a taxa adicional de transferência de calor para o gerador de vapor além daquela que seria requerida para produzir somente o vapor desejado na secagem? Qual é a diferença na potência líquida?
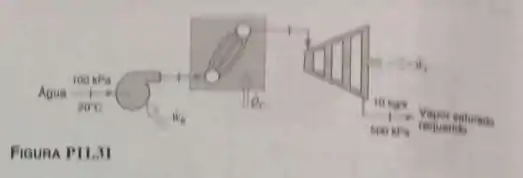
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
Nós temos os seguintes dados, fornecidos pelo enunciado
Assumimos que a compressão nas bombas é isentrópica. Então, . As perdas potenciais e cinéticas são desprezadas. A tarefa é determinar a transferência de calor adicional e a diferença na potência líquida. Primeiro vamos determinar a entalpia para todos os estados do ciclo, a
Para o estado (1), da tabela B.1.1 para a água saturada, nós obtemos que
Passo 2
Para o estado (4), em que a pressão é e vapor de vapor saturado da tabela B.1.2, obtemos que
Para o caso 1 se tivermos concentração em ciclo o fluxo é bombeado de 100 kPa para 5000 kPa. Determinando o trabalho da bomba no caso 1:
Substituindo os valores, nós temos que
Agora, a entalpia no estado (2):
Novamente, fazendo o processo de substituição
O trabalho específico na turbina:
Com isso, nós temos que
Passo 3
A entrada de calor no caso 1 é dado por
Com isso,
No caso 2 se não tivermos cogeração em ciclo, o fluxo é bombeado para a saída da turbina 500 kPa. Determinando o trabalho da bomba no caso 2:
Logo, nós temos que
Agora, a entalpia no estado (2):
E a entrada de calor no caso 2
Adição de transferência de calor no ciclo:
Substituindo os valores
A diferença na potência líquida:
Novamente, fazendo o processo de substituição