Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 4.Problemas - Ex. 32
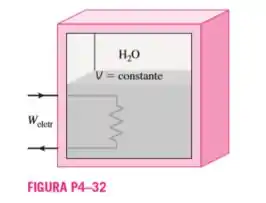
Um tanque rígido bem isolado contém 2 kg de uma mistura saturada de líquido e vapor de água a 150 kPa. Inicialmente, verifica-se que 3/4 da massa estão na fase líquida. Um resistor elétrico colocado no tanque é conectado a uma fonte de 110 V, e uma corrente de 8 A flui pelo resistor quando o interruptor é ligado. Determine quanto tempo levará para evaporar o líquido do tanque. Mostre também o processo em um diagrama que inclua as linhas de saturação.
Passo 1
Temos que o balanço de energia pode ser dado por:
Vamos fazer as seguintes considerações ao adotar o tanque rígido como sistema:
- O tanque é bem isolado, ;
- Desprezamos a variação da energia potencial e cinética do tanque, ;
Assim, temos que o balanço de energia ficaria da seguinte maneira:
Porém, temos que o trabalho elétrico pode ser dado por , onde . Assim,
Passo 2
O enunciado nos diz que temos uma mistura líquidovapor onde 3/4 da massa dessa mistura está na fase líquida, ou seja, o título da nossa mistura é de 0,25.
Consultando nas tabelas de vapor encontradas no final do livro conseguimos encontrar os seguintes valores de algumas propriedades:
Utilizando o título para calcular a energia interna e o volume específico no início do processo, temos:
Agora, ao final do processo, teremos que , então, basta encontrarmos na tabela a energia interna relacionada a esse volume específico. Ao olhar a tabela verificamos a necessidade de uma interpolação, daí:
Passo 3
Substituindo no balanço, temos:
Vamos usar o seguinte fator para converter a unidade para uma unidade de tempo:
Assim,
O diagrama TV ficará com o seguinte formato:
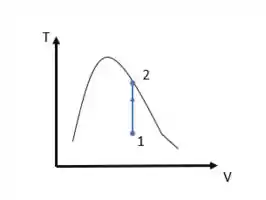
O diagrama nos mostra um processo com volume constante onde só a temperatura variou, o que aconteceu exatamente no nosso processo.
Resposta
Levaria 3630 s para evaporar o líquido do tanque.