O tanque sem tampa mostrado na F i g .P 2.56 é construído com aço e apresenta massa igual a 10 t o n e l a d a s . A área da seção transversal e a altura do tanque são iguais a 3m 2 e 16m . Determine a quantidade de concreto que deve ser introduzida no tanque para que esta flutue no oceano do modo indicado na figura.

Enunciado

Termodinâmica - Van Wylen- Ed: 6º - Capítulo 2.Problemas - Ex. 56

O tanque sem tampa mostrado na é construído com aço e apresenta massa igual a . A área da seção transversal e a altura do tanque são iguais a e . Determine a quantidade de concreto que deve ser introduzida no tanque para que esta flutue no oceano do modo indicado na figura.

Passo 1

Oi pessoal, tudo certo? Vamos analisar essa questão!

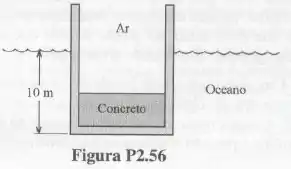
Bom... para que o tanque fique flutuando do modo indicado na figura (sua base a do nível do mar), as pressões na base do tanque e a abaixo do nível do mar devem ser iguais.

Ou seja, o tanque sofre força devido ao oceano nas paredes externas e devido ao ar mais concreto dentro do tanque.

A força no tanque devido ao oceano é de:

A força exercida dentro do tanque devido ao ar e ao concreto é dada por:

Passo 2

Essas forças devem ser iguais, portanto:

Isolando a massa de concreto, teremos a seguinte expressão:

Agora é só substituir:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Os balões geralmente são preenchidos com gás hélio, porque seu peso representa apenas um sétimo do ar em condições idênticas. A força de flutuação, que pode ser expressa como F B = ρ a r g V b a l ã o

Considere um peixe nadando 5 m abaixo da superfície livre da água. O aumento na pressão exercida sobre o peixe quando ele mergulha até a profundidade de 25 m abaixo da superfície livre é de196 Pa(b) 5

Considere uma piscina com 2 m de profundidade. A diferença de pressão entre a superfície e o fundo da piscina é de 12,0 kPa(b) 19,6 kPa(c) 38,1 kPa(d) 50,8 kPa(e) 200 kPa

As pressões atmosféricas na parte superior e inferior de um prédio são lidas por um barômetro como 96,0 e 98,0 kPa. Se a densidade do ar for de 1,0 kg/ m 3 , a altura do prédio será(a)17 m(b) 20 m(c)

A pressão atmosférica média na Terra é dada aproximadamente em função da altitude por meio da relação P a t m = 101,3251 - 0,02256 z 5,256 , onde P a t m é a pressão atmosférica em kPa, e z é a altitu