A temperaturas superiores a , o valor de para o cobre pode ser dado aproximadamente por uma relação linear da forma .
a) Da Fig. 3.10, encontre os valores de e .
b) Calcule a variação na entalpia específica do cobre a uma pressão de , quando a temperatura for aumentada de para .
Passo 1
Fala galerinha, beleza?
Começamos pelo item (a).
Precisamos olhar no gráfico da Fig. 3.10 a curva do calor específico do cobre para temperaturas acima de :
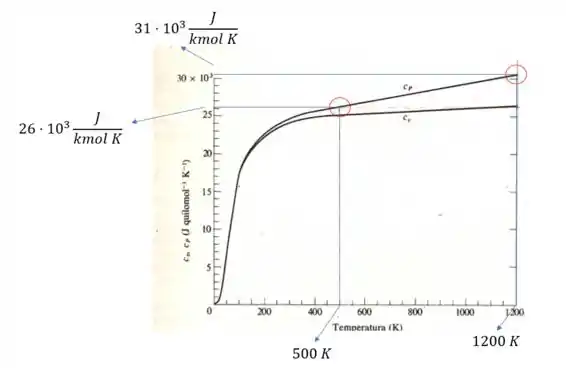
Para fazer o ajuste linear, consideramos os pontos circulados em vermelhos que correspondem a
Assim, podemos achar e substituindo os pontos na equação :
Resolvendo o sistema:
Passo 2
Agora vamos para o item (b).
Para calcular a variação da entalpia, basta lembrar que
Essencialmente, isso significa que a variação da entalpia é igual ao calor trocado em processos que ocorrem com pressão constante. Desta forma, podemos escrever
Logo,
Assim,
Fazendo as contas,
Essa é a variação de entalpia no processo.