Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 8.Problemas - Ex. 134

Um trocador de calor bem isolado deve aquecer água ( c p =   4,18   k J / k g . ° C ) de 25   ° C até 60   ° C a uma vazão de 0,4   k g / s . O aquecimento deve ser realizado por água geotérmica ( c p = 4,31   k J /   k g . ° C ) disponível a 140   ° C com fluxo de massa de 0,3   k g / s . O interior do tubo possui fina espessura e diâmetro de 0,6   c m . Determine (a) a taxa da transferência de calor e (b) a taxa de destruição de energia no trocador de calor.

Passo 1

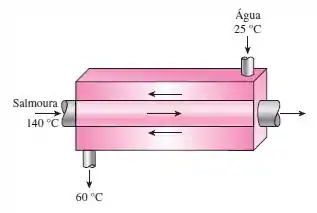
Vamos lá! A questão nos afirma que a água é aquecida em um trocador de calor por água geotérmica. A taxa de transferência de calor para a água e a taxa de destruição por esforço dentro do permutador de calor devem ser determinadas.

Assumindo que:

  1. Existem condições de funcionamento estáveis.
  2. O permutador de calor está bem isolado, de modo que a perda de calor para o ambiente é insignificante e, portanto, a transferência de calor do fluido quente é igual à transferência de calor para o fluido frio.
  3. Mudanças na cinética e as energias potenciais das correntes fluidas são insignificantes.
  4. As propriedades dos fluidos são constantes.
  5. A temperatura ambiente é de 25 ° C .

Os aquecedores específicos de água e fluido geotérmico são dados a 4,18 e 4,31   k J / k g . ° C , respectivamente.

Passo 2

Pronto já temos todas as informações necessárias, vamos para a análise. Desse modo temos que para o item (a) tomamos os tubos de água fria como o sistema, que é um volume de controle. O balanço energético para este sistema de fluxo constante pode ser expresso na forma de taxa como

E i n - E o u t = Δ E s y s t e m = 0

E i n = E o u t

Q i n + m h 1 = m h 2

Q i n = m c p ( T 2 - T 1 )

Então a taxa de transferência de calor para a água fria no permutador de calor torna-se

Q i n , a g u a   = m c p T o u t - T i n a g u a = 0.4 k g s 4.18 k J k g . ° C 60 ° C - 25 ° C = 58.52   k W

Observando que a transferência de calor para a água fria é igual à perda de calor da água geotérmica, a temperatura de saída da água geotérmica é determinada a partir

Q o u t = m c p T i n - T o u t g e o

T o u t = T i n - Q o u t m c p = 140 ° C - 58.52   k W 0.3 k g s 4.31 k J k g ° C = 94.7 ° C    

Passo 3

Já para o item (b) a taxa de geração de entropia dentro do permutador de calor é determinada aplicando a forma de taxa do balanço da entropia em todo o permutador de calor:

S i n - S o u t + S g e n = Δ S s y s t e m

m 1 s 1 + m 3 s 3 - m 2 s 2 - m 4 s 4 + S g e n = 0

m a g u a s 1 + m g e o s 3 - m a g u a s 2 - m g e o s 4 + S g e n = 0

S g e n = m a g u a s 2 - s 1 + m g e o ( s 4 - s 3 )

Observando que tanto a água doce como a geotérmica são substâncias incompressíveis, a taxa de geração de entropia é determinada como

S g e n = m a g u a c p ln ⁡ T 2 T 1 + m g e o c p ln ⁡ T 4 T 3 = 0.4 k g s 4.18 k J k g . K ln ⁡ 60 + 273 25 + 273 + 0.3 k g s 4.31 k J k g . K ln ⁡ 94.7 + 273 140 + 273

= 0.0356   k W / K    

A energia destruída durante um processo pode ser determinada a partir de um balanço de energia ou diretamente a partir de sua definição X d e s t r o y e d   =   T 0 S g e n ,

X d e s t r o y e d = T 0 S g e n = 298   K 0.0356 k W K = 10.61   k W

Resposta

a )   Q i n = 58.52   k W

b )   X d e s t r o y e d = 10.61   k W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A energia de um sistema fechado pode ser negativa? E quanto ao fluxo de energia? Justifique sua resposta usando uma substância incompressível como exemplo.
Gás argônio se expande de 3,5 MPa e 100 °C até 500 kPa em uma válvula de expansão adiabática. Considerando condições ambientais de 100 kPa e 25 °C, determine (a) a energia do argônio na entrada, (b) a
Água líquida entra em uma tubulação adiabática a 15° C a uma taxa de 3k g / s . Observa-se que a temperatura da água se eleva em 0,3° C na tubulação devido ao atrito. Considerando que a temperatura do
Escrevendo as equações da primeira e da segunda lei (e simplificando), obtenha uma expressão para o trabalho reversível de um sistema fechado que troca calor com a vizinhança a T 0 na quantidade Q 0 e
Água entra em uma bomba a 100 kPa e 30 °C a uma vazão de 1,35 kg/s, saindo a 4 MPa. Considerando que a bomba tem eficiência isentrópica de 70%, determine (a) o consumo real de potência, (b) a taxa de