Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 8.Problemas - Ex. 128

Vapor de agua deve ser condensado no condensador de uma usina de potência a vapor a uma temperatura de 45   ° C com agua de resfriamento de um lago próximo, que entra nos tubos do condensador a 12   ° C a uma vazão de 330   k g / s e sai a 20   ° C . Considerando que o condensador está perfeitamente isolado, determine (a) a taxa de condensação do vapor de agua e (b) a taxa de destruição de energia no condensador.

Passo 1

Vamos lá! A questão nos afirma que o vapor é condensado pela água de arrefecimento no condensador de uma central eléctrica. A taxa de condensação do vapor e a taxa de destruição por esforço devem ser determinadas.

Podemos representar o problema como:

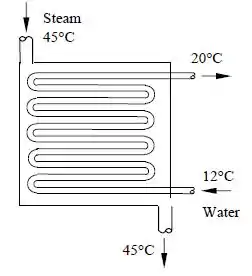
Assumindo que:

  1. Existem condições de funcionamento estáveis.
  2. O permutador de calor está bem isolado, de modo que a perda de calor para o ambiente é insignificante e, portanto, a transferência de calor do fluido quente é igual à transferência de calor para o fluido frio.
  3. As alterações na cinética e nas energias potenciais dos fluxos de fluido são negligenciáveis.
  4. As propriedades dos fluidos são constantes.

A entalpia e entropia de vaporização da água a 45 ° C são h f g = 2394,0   k J / k g e s f g = 7,5247 kJ/kg.K (Tabela A-4). O calor específico da água à temperatura ambiente é c p = 4,18   k J / k g . ° C (Tabela A-3).

Passo 2

Pronto já temos todas as informações necessárias, vamos para a análise. No item (a) Tomamos os tubos de água fria como o sistema, que é um volume de controle. O balanço energético para este sistema de fluxo constante pode ser expresso na forma de taxa como

E i n - E o u t = Δ E s i s t e m a = 0

Logo,

E i n = E o u t

Q i n + m h 1 = m h 2

Q i n = m c p

Então a taxa de transferência de calor para a água de arrefecimento no condensador torna-se

Q = m c p T o u t - T i n = 330 ⋅ 4.18 ⋅ 20 - 12 = 11035   k J / s

A taxa de condensação de vapor é determinada como sendo

Q = m h f g → m = Q h f g = 11035 2394 = 4.61   k g / s

Passo 3

Certo, agora vamos para o item (b), desse modo, observe que a taxa de geração de entropia dentro do condensador durante este processo pode ser determinada pela aplicação da forma de taxa do balanço de entropia em todo o condensador. Observando que o condensador está bem isolado e, portanto, a transferência de calor é insignificante, o balanço de entropia para este sistema de fluxo constante pode ser expresso como

S i n - S o u t + S g e n = Δ S s i s t e m a = 0

Portanto,

m 1 s 1 + m 3 s 3 - m 2 s 2 - m 4 s 4 + S g e n = 0

m s 1 + m s 3 - m s 2 - m s 4 + S g e n = 0

S g e n = m a g u a s 2 - s 1 + m v a p o r ( s 4 - s 3 )

Observando que a água é uma substância incompressível e que o vapor muda de vapor saturado para líquido saturado, a taxa de geração de entropia é determinada como

S g e n = m a g u a c p ln ⁡ T 2 T 1 + m v a p o r s f - s g = m a g u a c p ln ⁡ T 2 T 1 - m v a p o r s f g

= 330 4.18 ln ⁡ 20 + 273 12 + 273 - 461 7.5247 = 3.501   k W / K

Então a energia destruída pode ser determinada diretamente de sua definição X d e s t r u í d a   =   T 0 S g e n , logo

X d e s t r u i d a = T 0 S g e n = 285 3.501 = 998   k W

Resposta

a )   Q = 4.61   k g / s

b )   X d e s t r u í d a = 998   k W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere uma garrafa rígida de 12L evacuada e exposta a atmosfera a 100k P a e 1 7° C . Em um processo, uma válvula no gargalo da garrafa e aberta e o ar atmosférico escoa para dentro da garrafa. O a
Um tanque de volume constante contem 20k g de nitrogênio a 1.000K , e um dispositivo mantido a uma pressão constante contem 10k g de argônio a 300K . Uma máquina térmica colocada entre o tanque e o di
Uma tonelada de água liquida a 65° C e colocada em uma sala bem isolada e bem vedada de 3m ×4m×7m que está inicialmente a 16° C e 100k P a . Considerando calores específicos constantes para o ar e a á
Um tanque rígido bem isolado de 100L está inicialmente preenchido com nitrogênio a 1.000k P a e 20° C . Uma válvula e então aberta, e metade da massa do nitrogênio escapa. Determine a mudança no conte
Um arranjo pistão-cilindro sem atrito, mostrado na Fig. P8-123, contêm inicialmente 0,01m 3 de gás argônio a 400K e 350k P a . Calor e transferido para o argônio de uma fornalha a 1.200K , e o gás exp