Enunciado

Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 16.Problemas - Ex. 86

Usando os dados da função de Gibbs, determine a constante de equilíbrio para o processo de dissociação a 2000 K. Compare seu resultado com o valor de listado na Tab. A-28.

Passo 1

Tá legal! Sabemos que o valor da constante de equilíbrio pode ser determinada a partir da equação 16-14 apresentada nessa seção, que nos fornece:

Então, precisamos calcular o termo da exponencial. Dessa forma, começando com , temos, conforme vimos na equação 16-11:

E, abrindo as expressões, temos:

Então, substituindo os valores conhecidos, pegando os dados das entalpias e entropias de formação do apêndice A, temos:

Passo 2

Agora, substituindo os valores conhecidos na equação do passo 1, temos:

Passo 3

Agora, consultando a tabela A-28, temos:

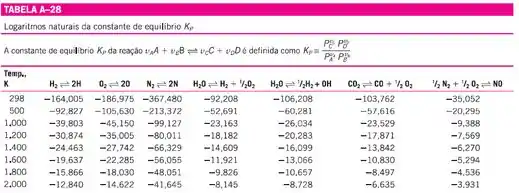
O valor presente na tabela é o logarítmo natural de , então, pegando o do passo 2 e aplicando o logarítmo natural, temos:

Esse valor é próximo do valor de de -14,622 apresentado na tabela A-28.

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

44 Um conjunto cilindro – pistão opera a pressão constante e contém 0,2 kg de água. Inicialmente, a água se encontra como vapor saturado a 400 kPa. O conjunto é então resfriado até que o volume ocupad

43 Um conjunto cilindro – pistão, que apresenta esbarro, contém 50 kg água. Inicialmente, o volume e a pressão na água são iguais a 0,1 m3 e 200 kPa. Quando o pistão encosta no esbarro, o volume da câ

40 Um conjunto cilindro – pistão contém 1 kg de água. Inicialmente, a temperatura da água e o volume interno do conjunto são iguais a 20°C e 0,1 m3. O pistão então é travado e tranfere-se calor à água

46 Uma massa de 25 kg se desloca a 25 m/s. Um freio é acionado e a massa é imobilizada em 5 segundos num movimento que apresenta desaceleração constante. A energia armazenada no freio é então transfer

47 Um conjunto cilindro – pistão isolado termicamente contém R-12 a 25°C e título de 90%. O volume, neste estado, é 45 litros. Permite-se o movimento do pistão e o R-12 expande até que atinja o estado