Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Termodinamica,Teoria Cinética e Termodinâmica Estatística, Sears e Salinger- Ed: 3º - Capítulo 2.Problemas - Ex. 35

(a) use o fato de d v ser uma diferencial exta e as definições de β   e   k para provar que

∂ β ∂ P T = - ∂ k ∂ T P

(b) da figura 2-16, obtenha uma equação linear que dê aproximadamente a relação entre k   e   T para o cobre a uma pressão constante de 1   a t m   e   a   T = 1000   K .

( c ) calcula a variação do coeficiente de dilatação do cobre com a pressão e a temperatura constante.

(d) calcule o coeficiente de dilatação do cobre a 1000   K   e   1   a t m , e calcule a variação fracionária do volume do cobre, quando a pressão é aumentada isotermicamente para 100   a t m . Suponha que ∂ β ∂ P r seja independente da pressão.

Passo 1

Falaaaaa rapaziada tudo blz?

Nessa questão do livro de termodinâmica de Sears e Salinger ele deseja determinar:

(a) use o fato de d v ser uma diferencial exta e as definições de β   e   k para provar que

∂ β ∂ P T = - ∂ k ∂ T P

(b) da figura 2-16, obtenha uma equação linear que dê aproximadamente a relação entre k   e   T para o cobre a uma pressão constante de 1   a t m   e   a   T = 1000   K .

( c ) calcula a variação do coeficiente de dilatação do cobre com a pressão e a temperatura constante.

(d) calcule o coeficiente de dilatação do cobre a 1000   K   e   1   a t m , e calcule a variação fracionária do volume do cobre, quando a pressão é aumentada isotermicamente para 100   a t m . Suponha que ∂ β ∂ P r seja independente da pressão.

Precisa ficar assim não meus abençoados conforme você for vendo os passos vai perceber que ela é de boa.

Passo 2

Então galera para determinarmos o que foi pedido nas opções, devemos saber a equação de Van der Waals definida por,

∂ p ∂ v T = 0         e         ∂ 2 p ∂ v 2 T = 0

Ficando na letra (a) para provar que,

∂ β ( ∂ p T = ∂ k ∂ t p

Temos que,

∂ p ∂ v T = - R T v - b 2 + 2 a v 3

Ficando,

∂ 2 p ∂ v 2 T = - 2 R T v - b 3 - 6 a v 4

Como ∂ 2 p ∂ v = ∂ 2 k 0 ∂ T e definindo P = β   e   k 0 = k , temos

∂ β ∂ p T = - ∂ k ∂ T P

Já na letra (b) dada a figura,

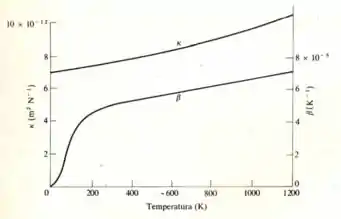
Temos,

∂ v ∂ p P = n R T p 2

Com, n = 1   x   10 - 12     R = 1     P 2 = 1     e     t = 6,4

Ficando,

∂ v ∂ p T = 10 - 12   x   1   x   6,4 1 = 6,4   x   10 - 12

Na letra ( c ) para se determinar a variação do coeficiente de dilatação temos que,

k = 1 V ∂ V ∂ P T

Com,

V = 3,3   x   10 15 e ∂ V ∂ P T = 1

Ficando,

k = 1 3,3   x   10 15   x   1 = 3,3   x   10 - 15

E por fim na letra (d) para calcular o coeficiente de dilatação do cobre 1000   K   e   1   a t m temos,

∂ V = P . T

Com,

T = 5,2   x   10 - 3           P = 1 a t m

Ficando,

∂ V = 5,2   x   10 - 3   x   1 = 5,2   x   10 - 3

Espero que eu tenha ajudado e te vejo no próximo desafio.

Até a próxima.

Resposta

a) ∂ β ∂ p T = - ∂ k ∂ T P

b) ∂ v ∂ p T = 6,4   x   10 - 12

c) k = 3,3   x   10 - 15

d) ∂ V = 5,2   x   10 - 3

Exercícios de Livros Relacionados

Para que um sistema esteja em equilíbrio termodinâmico, a temperatura e a pressão precisam ser as mesmas em todos os lugares?
O tubo em J, de seção reta uniforme, na Fig. 2.19, contem a ar a pressão atmosférica. A altura barométrica é h 0 . E derramando mercúrio no lado aberto, encerrado o ar na extremidade do lado fechado.
Use a relação do problema anterior para mostrar que os dados dos problemas 2.24e2.25 são consistentes.
Mostrar que o momento magnético, M , de um material paramagnético é uma função de estado, ao mostrar que d M é uma diferencial exata.