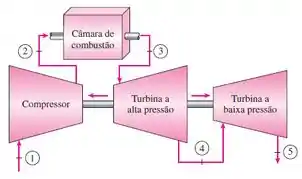
Uma usina de potência com turbina a gás opera em um ciclo Brayton modificado como mostrado na figura seguinte, com uma razão de pressão total igual a . Ar entra no compressor a e . A temperatura máxima do ciclo é de . O compressor e as turbinas são isentrópicas. A turbina de alta pressão desenvolve potência suficiente para operar o compressor. Considere as propriedades constantes para o ar a , com , , , .
(a) Represente graficamente o diagrama para o ciclo. Identifique os estados.
(b) Determine a temperatura e a pressão no estado à saída da turbina de alta pressão.
(c) Considerando que a produção de potência líquida é de , determine a vazão mássica do ar dentro do compressor, em .
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Observando a figura do enunciado, podemos representar o sistema modificando da seguinte maneira em um diagrama :
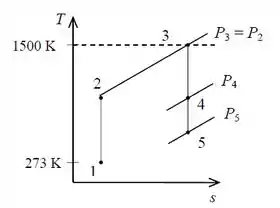
Levando em consideração que o Ar entra no compressor a e representado pelo estado e a temperatura máxima do ciclo é de que é representada pelo estado em um ciclo Brayton.
Passo 2
Agora vamos analisar os processos:
O processo é uma compressão isentrópica, logo:
Temos que:
Nos foi dito que a razão de pressão é de , portanto:
Logo:
Substituindo os valores temos que:
Passo 3
Como a turbina e o compressor são montados no mesmo eixo, a entrada de energia do compressor é igual à potência de saída da turbina. Logo:
Ou:
Substituindo os valores, temos que:
Passo 4
Podemos calcular a pressão do estado a partir da relação do processo isentrópico. Para a expansão , temos que:
Agora fique atento para não se perder, vamos fazer algumas considerações.
Observando a equação acima, temos os valores de , e . Como queremos o valor de , precisamos descobrir antes, o valor de .
Sabemos que na câmara de combustão (processo ), a pressão é constante. Ou seja:
Já sabemos também que:
Portanto, podemos dizer que:
E como sabemos o valor de , podemos dizer que:
Portanto:
Passo 5
Vamos analisar agora o processo , pois é lá que se dá a produção de potência líquida. Sabemos que:
Ou seja, precisamos descobrir o valor de , para encontrar que é solicitado no item “c”.
Da expansão isentrópica , temos que:
Como a pressão na saída da turbina de baixa pressão deve ser a mesma de entrada do compressor, temos que:
Logo:
Substituindo os valores, temos que:
Portanto: