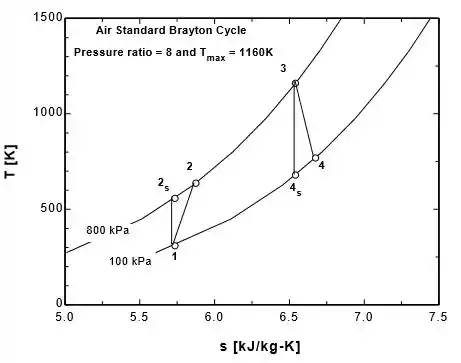
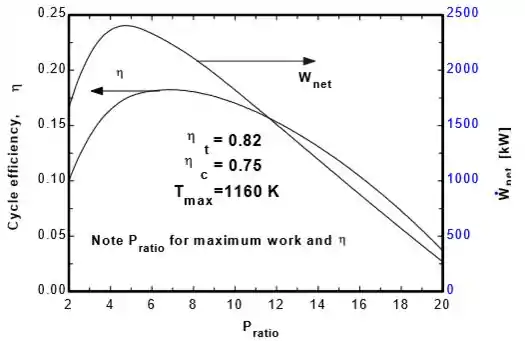
Repita o Prob. 9–191 considerando a variação dos calores específicos do ar com a temperatura.
Passo 1
Utilizando o EES:
"Dados de entrada - da janela do diagrama"
{P_ratio = 8}
{T[1] = 300 [K]
P[1] = 100 [kPa]
T[3] = 800 [K]
m_dot = 1 [kg / s]
Eta_c = 75/100
Eta_t = 82 / 100}
“Condições de entrada”
h[1]=ENTHALPY(Air,T=T[1])
s[1]=ENTROPY(Air,T=T[1],P=P[1])
"Análise do compressor"
s_s[2] = s[1] "Para o caso ideal, as entropias são constantes no compressor"
P_ratio = P[2] / P[1] "Definição da razão de pressão - para encontrar P [2]"
T_s[2] = TEMPERATURE(Air, s = s_s[2], P = P[2]) "T_s [2] é o valor isentrópico de T [2] na saída do compressor"
h_s[2] = ENTHALPY(Air, T = T_s[2])
Eta_c = (h_s[2]-h[1]) / (h[2]-h[1]) "Eficiência adiabática do compressor; Eta_c = W_dot_c_ideal/W_dot_c_actual."
m_dot * h [1] + W_dot_c = m_dot * h [2] "Primeira lei SSSF para o compressor real, assumindo: adiabático, ke = pe = 0"
"Análise externa do trocador de calor"
P[3] = P[2] "o processo 2-3 é SSSF pressão constante "
h[3] = ENTHALPY(Air, T = T[3])
m_dot * h[2] + Q_dot_in = m_dot *h[3] " Primeira Lei SSSF para o trocador de calor, assumindo W = 0, ke = pe = 0 "
" Análise da turbina "
s[3] = ENTROPY (Air, T = T[3], P = P[3]) s_s[4] = s[3] " Para o caso ideal, as entropias são constantes através da turbina "
P_ratio = P[3] / P[4]
T_s[4] = TEMPERATURE (Air, s = s_s[4], P = P[4]) " Ts [4] é o valor isentrópico de T [4 ] na saída da turbina "
h_s[4] = ENTHALPY (Air, T = T_s[4]) " Eta _t = eficiência adiabática da turbina W_dot_t / Wts_dot, Wts_dot> W_dot_t "
Eta_t = (h[3] -h[4]) / (h[3] -h_s[4])
m_dot * h[3] = W_dot_t + m_dot * h[4] "Primeira lei SSSF para o compressor real, assumindo: adiabático, ke = pe = 0"
"Análise de ciclo"
W_dot_net = W_dot_t-W_dot_c "Definição do trabalho em ciclo líquido, kW"
Eta = W_dot_net / Q_dot_in "Eficiência térmica do ciclo"
Bwr = W_dot_c / W_dot_t "Relação de trabalho de retorno"
"Os seguintes pontos de estado são determinados apenas para produzir um gráfico T-s "
T[2]=temperature('air',h=h[2])
T[4]=temperature('air',h=h[4])
s[2]=entropy(air,T=T[2],P=P[2])
s[4]=entropy(air,T=T[4],P=P[4])
Passo 2
A tabela e os gráficos serão:

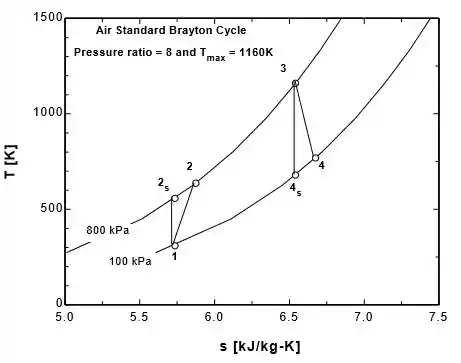
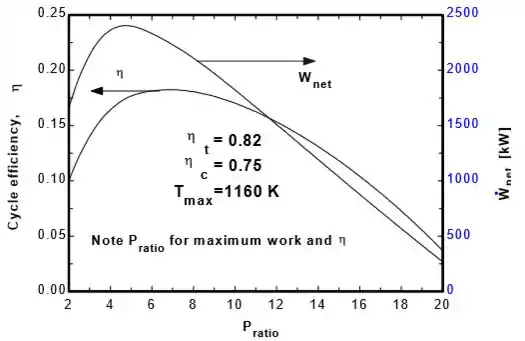
Resposta