Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Sonntag, R.E. e Borgnakke, C. -Fundamentos da Termodinâmica- Ed: 1º - Capítulo 6.Problemas - Ex. 64

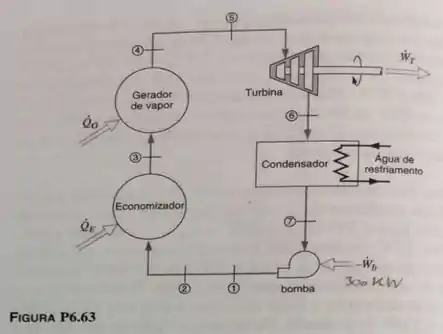
Para a usina termelétrica a vapor mostrada no Problema 6.63, considere que a água de refrigeração vem de um lado a 15   ° C e retorna a 25   ° C . Determine a taxa de transferência de calor no condensador e a vazão mássica da água de refrigeração proveniente do lago

Passo 1

Fala galeraaa!

Vamos começar com a parte conceitual...

Sabemos que os diâmetros das tubulações são de 200   m m , do gerador de vapor até a turbina, e de 75   m m , do condensador até o economizador e gerador de vapor...

Pois muito bem! Vamos começar calculando então, a área da seção transversal do condensador...

A 7 = π 4 d 7 2

Como...

d 7 = 75   m m = 0,075   m

Então;

C o n d e n s a d o r ∴ A 7 = π 4 d 7 2 = π 4 0,075   m 2 = 0,04418   m ²

Passo 2

Pois muito bem! Sabendo então a área do condensador, vamos calcular a velocidade V 7 com que o vapor passa pela turbina no estado 7...

V 7 = m ˙ v 7 A 7

Onde o volume específico nas condições especificadas em 7, é dado por...

v 7 = 0,01008   m ³ / k g

Como podemos ver na seguinte tabela que contem os volumes específicos para cada uma das condições mostradas na figura da tabela do enunciado...

Logo;

V 7 = 25 ⋅ 0,001008 0,04418

V 7 = 5,7   m / s

Em seguida, vamos calcular o valor da entalpia no estado 6 dado que sabemos o título de 92 % :

h 6 = h 6 l + x ( h 6 v - h 6 l )

h 6 = 191,83 + 0,92 ⋅ 2392,8

h 6 = 2393,2   k J / k g

Passo 3

Assim, usando a equação de energia para o volume de controle em condensadores considerando os estados 6 e 7... Obtemos que:

Q ˙ c o n d + m ˙ h 6 + m ˙ V 6 2 2 = m ˙ h 7 + m ˙ V 7 2 2

Q ˙ c o n d = m ˙ h 7 - m ˙ h 6 + m ˙ ( V 7 2 - V 6 2 ) 2

Então, substituindo os valores numéricos encontramos nossa resposta...

Q ˙ c o n d = 25 167,57 - 2393,2 - 200 2 - 5,7 2 2 ⋅ 1000

Q ˙ c o n d = - 56140   k W

Passo 4

Dessa forma, usando a tabela A.2 para a água saturada...

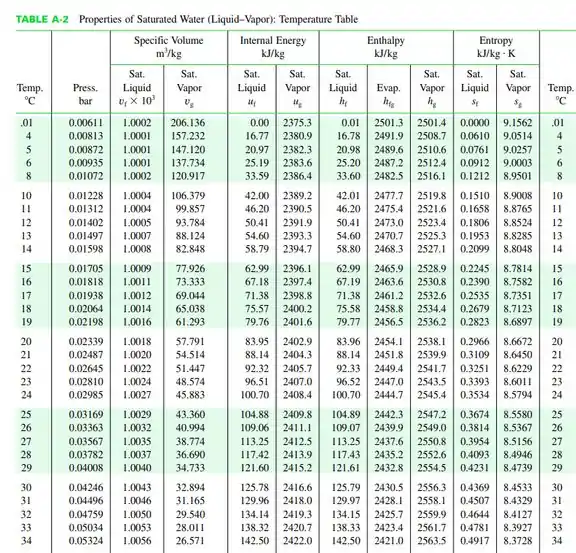
Conseguimos encontrar a vazão mássica da água de refrigeração proveniente do lago dado que a quantidade de calor do condensador também pode ser escrita como...

Q ˙ c o n d = m ˙ H 2 O ( h s a í d a - h e n t r a d a )

Onde h s a í d a e h e n t r a d a são as entalpias correspondentes considerando que a água de refrigeração vem de um lado a 15   ° C e retorna a 25   ° C ... Ou seja;

h s a í d a = 104,9   k J / k g

h e n t r a d a = 63,0   k J / k g

Assim, temos que...

Q ˙ c o n d = m ˙ H 2 O ( h s a í d a - h e n t r a d a )

m ˙ H 2 O = Q ˙ c o n d h s a í d a - h e n t r a d a

m ˙ H 2 O = 56140 104,9 - 63

m ˙ H 2 O = 1339,9   k g / s

Passo 5

Obtido a massa de água, vamos então dar atenção ao economizador... Como podemos ver na tabela do passo 2, em 2 temos as mesmas condições de 7... Logo, a velocidade é a mesma...

v 2 ≅ v 7 = 5,7   m / s

E também podemos calcular as velocidades correspondentes para os estados 3 e 4...

V 3 = 25 ⋅ 0,0011 0,04418

V 3 = 6,3   m / s

V 4 = 25 ⋅ 0,0598 0,04418

V 4 = 47,9   m / s

Passo 6

Com isso, somos capazes de encontrar a taxa de transferência de calor no economizador...

Q ˙ e c o n = m ˙ ( h 4 - h 3 )

Q ˙ e c o n = 25 ( 744 - 193,7 )

Q ˙ e c o n = 13755   k W

E no gerador de vapor...

Q ˙ g e r + m ˙ h 3 + m ˙ V 3 2 2 = m ˙ h 4 + m ˙ V 4 2 2

Q ˙ g e r = m ˙ h 4 - m ˙ h 3 + m ˙ ( V 4 2 - V 3 2 ) 2

Então, substituindo os valores numéricos encontramos nossa resposta...

Q ˙ c o n d = 25 3426 - 744 + 47,9 2 - 6,3 2 2 ⋅ 1000

Q ˙ c o n d = 67072   k W

Resposta

Q ˙ c o n d = - 56140   k W

m ˙ H 2 O = 1339,9   k g / s

Exercícios de Livros Relacionados

Não há nenhuma energia armazenada no capacitor do circuito da Figura P7.77 quando a chave 1 se fecha em t = 0. A chave 2 fecha‑se 2,5 milissegundos mais tarde. Determine vo(t) para t $ 0.
Um voltímetro com um fundo de escala de 10 V é usado para medir a tensão de saída no circuito da Figura P5.7. Qual é a leitura do voltímetro? Admita que o amp op seja ideal.
O capacitor no circuito mostrado na Figura P7.87 está carregado com 20 V, no instante em que a chave é fechada. Se o dielétrico do capacitor se rompe (perde suas características isolantes) quando a te
A chave no circuito da Figura P7.88 esteve fechada por um longo tempo. A tensão máxima nominal do capacitor de 1,6 mF é 14,4 kV. Em quanto tempo, depois da abertura da chave, a tensão no capacitor alc
Não há nenhuma energia armazenada no capacitor do circuito da Figura P7.77 quando a chave 1 se fecha em t = 0. A chave 2 fecha‑se 2,5 milissegundos mais tarde. Determine vo(t) para t $ 0.