Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Sonntag, R.E. e Borgnakke, C. -Fundamentos da Termodinâmica- Ed: 1º - Capítulo 6.Problemas - Ex. 65

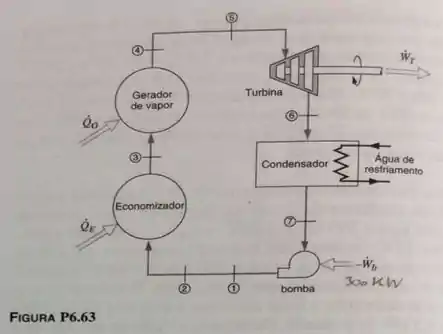
Para a usina termelétrica a vapor mostrada no Problema 6.63, determine a taxa de transferência de calor no economizador, que é um trocador de calor de baixa temperatura. Determine também a taxa de transferência de calor necessária no gerador de vapor.

Passo 1

Fala galeraaa!

Vamos começar com a parte conceitual...

Sabemos que os diâmetros das tubulações são de 200   m m , do gerador de vapor até a turbina, e de 75   m m , do condensador até o economizador e gerador de vapor...

Pois muito bem! Vamos começar calculando então, a área da seção transversal do economizador e do gerador...

E c o n o m i z a d o r ∴ A 3 = π 4 d 3 2

G e r a d o r ∴ A 4 = π 4 d 4 2

Como...

d 3 = 75   m m = 0,075   m

d 4 = 200   m m = 0,2   m

Então;

E c o n o m i z a d o r ∴ A 3 = π 4 d 3 2 = π 4 0,075   m 2 = 0,04418   m ²

G e r a d o r ∴ A 4 = π 4 d 4 2 = π 4 0,2   m 2 = 0,03142   m ²

Passo 2

Pois muito bem! Sabendo então a área do economizador e do gerador, vamos calcular a velocidades V 3 e V 4 com que o vapor passa pela turbina nos estado 3 e 4...

V 3 = m ˙ v 3 A 3

V 4 = m ˙ v 4 A 4

E o volume específico a gente consegue extrair das nossas tabelas termodinâmicas correspondentes... No caso, temos para os estados 3 e 4 que...

v 3 = 0,0011   m ³ / k g

v 3 = 0,0598   m ³ / k g

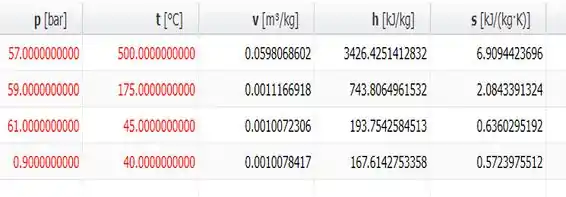
Logo;

V 3 = m ˙ v 3 A 3 = 25 ⋅ 0,0011 0,04418

V 3 = 6,3   m / s

Como podemos ver aí, o valor de V 3 foi quase igual ao da velocidade em V 2 que a gente achou no item anterior que foi de...

V 2 = 5,7   m / s

Quanto à V 4 ;

V 4 = m ˙ v 4 A 4 = 25 ⋅ 0,0598 0,04418

V 4 = 47,9   m / s

Passo 3

Com isso, somos então capazes de encontrar a taxa de transferência de calor no economizador...

Q ˙ e c o n + m ˙ h 2 + m ˙ V 2 2 2 = m ˙ h 3 + m ˙ V 3 2 2

Q ˙ e c o n = m ˙ h 3 - h 2 + m ˙ V 3 2 - V 2 2 2 ⋅ 1000

Q ˙ e c o n = 25 744 - 193,7 + 6,3 2 - 5,7 2 2 ⋅ 1000

Q ˙ e c o n = 13757,6   k W

E no gerador de vapor...

Q ˙ g e r + m ˙ h 3 + m ˙ V 3 2 2 = m ˙ h 4 + m ˙ V 4 2 2

Q ˙ g e r = m ˙ h 4 - m ˙ h 3 + m ˙ ( V 4 2 - V 3 2 ) 2

Q ˙ c o n d = 25 3426 - 744 + 47,9 2 - 6,3 2 2 ⋅ 1000

Q ˙ c o n d = 67072   k W

Resposta

Q ˙ e c o n = 13755   k W

Q ˙ c o n d = 67072   k W

Exercícios de Livros Relacionados

Um trocador de calor adiabático é usado para aquecer água fria a 15 °C, a qual entra a uma taxa de 5 kg/s por meio de ar quente a 90 °C – que também entra no trocador a uma taxa de 5 kg/s. Considerand
A fonte de tensão no circuito da Figura P7.83(a) está gerando o sinal mostrado na Figura P7.83(b). Não há nenhuma energia armazenada em t=0.Determine as expressões para v 0 ( t ) que sejam válidas par
Para a usina termelétrica a vapor mostrada no Problema 6.63, considere que a água de refrigeração vem de um lado a 15° C e retorna a 25° C . Determine a taxa de transferência de calor no condensador e
Para manter um motor a jato refrigerado, uma tomada de ar é feita externamente à câmara de combustão. Admita que 2k g / s de ar quente a 2000K e 500k P a sejam misturados com 0,5k g / s de ar a 500K e