Vapor de água superaquecido a 180 psia e 500 °F é resfriado a volume constante até que a temperatura caia para 250 °F. No estado final, determine
- a pressão
- o título
- a entalpia.
Mostre também o processo em um diagrama T-v que inclua as linhas de saturação.
Passo 1
A questão fala sobre um processo de resfriamento que ocorre com a água. A água vai da pressão inicial e da temperatura inicial até a temperatura final menor . Nesse processo, o volume da água permanece constante. Logo, seu volume inicial é igual ao seu volume final (depois do resfriamento) . A figura abaixo ilustra o estado inicial 1 da água, seu processo de resfriamento e o estado final 2 da água.
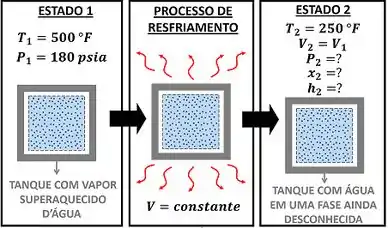
A questão quer saber primeiro a pressão final da água , depois ela quer saber o título final da água , em terceiro lugar ela quer o valor da entalpia da água e, por fim, ela quer que a gente desenhe um gráfico - (temperatura versus volume específico) do processo de resfriamento da água.
Faremos tudo isso usando as tabelas de propriedade da água (tabelas A-4E e A-6E do apêndice 2 do livro).
Passo 2
Esse primeiro passo é a primeira parte para encontrar a pressão final da água (letra (a) da questão).
Faremos isso usando a tabela de propriedades da água para o estado 2. No entanto, para usar a tabela para o estado 2, precisamos conhecer o valor de duas propriedades intensivas (que não dependem da massa do sistema) do estado 2. Nesse momento só conhecemos o valor da temperatura .

Para conseguir o valor de outra propriedade intensiva precisamos nos lembrar de dois fatos. Um é que o processo de resfriamento é a volume constante. Logo:
O outro fato é que, durante o processo de resfriamento, o tanque de água não recebe massa nem perde massa. Isso significa que a massa de água presente no tanque no estado 1 é igual à massa de água presente no tanque no estado 2.
Como e , a divisão de por é igual à divisão de por .
Como o volume específico é igual ao volume dividido pela massa , encontramos que:
Ou seja, o volume específico final do estado 2 é igual ao volume específico do estado 1 . Isso quer dizer que, se a gente encontrar o valor de através da tabela termodinâmica da água, encontramos o valor de também. Desta forma, conseguimos encontrar a segunda propriedade intensiva do estado 2 que restava e poderemos usar a tabela de propriedades para o estado 2.
Passo 3
Esse segundo passo é a segunda parte para encontrar o valor da pressão final (letra (a) da questão).
Descobrimos que, para achar o valor de , temos que encontrar o valor do volume específico inicial da água .
Isso é feito usando a tabela de vapor superaquecido da água (tabela A-6E do apêndice 2 do livro). O valor de está na parte da tabela destinada à pressão de , na mesma linha que a temperatura de e na mesma coluna que .
Logo:
Agora podemos usar a tabela de propriedades da água para o estado 2 e achar . Mas qual das tabelas devemos usar?
Se o volume específico da água for menor que o volume específico da água líquida saturada a , a água do estado 2 é um líquido comprimido e usaremos uma tabela de água líquida comprimida.
Se o volume específico da água for maior que o volume específico do vapor d’água saturado a , a água do estado 2 é um vapor superaquecido e usaremos uma tabela de vapor d’água superaquecido.
Se o volume específico da água estiver entre e , a água do estado 2 está saturada e usaremos a tabela de saturação da água.
Para achar e e descobrir qual tabela devemos usar para achar , consultaremos a tabela de saturação A-4E da água do apêndice 2 do livro. está na mesma linha que a temperatura de e na mesma coluna que . está na mesma linha que a temperatura de e na mesma coluna que .
Comparando com e , vemos que está entre esses dois termos. Logo, a água está saturada no estado final 2 e precisamos usar a tabela de saturação para achar .
Como a água está saturada neste estado 2, é a pressão de saturação da água para a temperatura . Usando a tabela de saturação (tabela A-4E do livro), vemos que a pressão está na mesma linha da temperatura de e na mesma coluna que .
Passo 4
Nesse passo, acharemos o título da água no estado 2 e, desta forma, resolveremos a letra (b) da questão.
O título da água é a fração de vapor que existe na água saturada, quando ela se encontra no estado 2 (após o resfriamento). Esse valor depende dos termos e encontrados no passo anterior. Como já possuímos esses termos, podemos achar .
Como o título da água no estado 2 vale , a água do estado 2 é formada por de vapor saturado e de líquido saturado.
Passo 5
Nesse passo, acharemos a entalpia da água no estado 2 e, desta forma, resolveremos a letra (c) da questão.

Como a água no estado 2 é formada por de vapor saturado e de líquido saturado, a entalpia é formada pela entalpia do vapor saturado e pela entalpia do líquido saturado . Uma forma de mostrar que é uma mistura de e é através da fórmula abaixo.
e são encontrados na tabela A-4E de saturação da água.
está na mesma linha que a temperatura de e na mesma coluna que . está na mesma linha que a temperatura de e na mesma coluna que .
Substituindo esses dois valores na equação de , achamos:
Passo 6
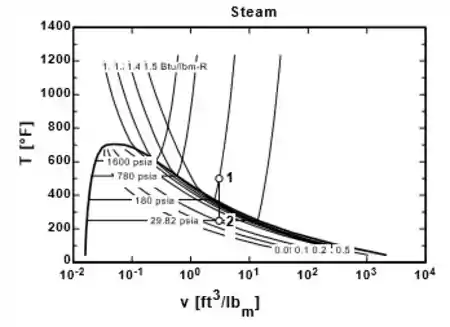
O gráfico - que mostra o processo de resfriamento da água do estado 1 ao estado 2 se encontra abaixo.
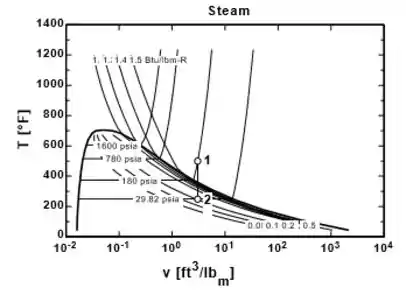
Nele, vemos que o ponto 1 se encontra logo acima do ponto 2, porque e .
Resposta