Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Van Wylen- Ed: 6º - Capítulo 3.Problemas - Ex. 41

Um vaso de pressão rígido e selado é destinado ao aquecimento de água. O volume do vaso é 1 m 3 e contém, inicialmente, 2   k g de água a 100 ° C . Qual deve ser a regulagem da válvula de segurança (pressão de abertura) de modo que a temperatura máxima da água no tanque seja igual a 200 ° C .

Passo 1

Temos um processo que o volume é constante. A água não sai do vaso do primeiro estado para segundo logo temos volume constante.

Para determinarmos a pressão de abertura teremos que reconhecer nas tabelas a qual pressão corresponde ao volume específico que temos.

Passo 2

Como assim? Nós notamos que nosso volume permanece constante, portanto, o volume específico também.

Como enunciado nos deu massa e volume, partiu calcular ele.

v = m V = 1   m 3 2   k g = 0,5   m 3 / k g

Passo 3

Com o volume específico em mãos e também à temperatura de estado final que é 200 ° C , vamos à tabela B . 1.3 . Devemos procurar o volume de 0,5   m 3 / k g sobe a nossa temperatura final.

Note que temos dois candidatos interessantes para escolha estamos em 400   k P a e 500 k P a .

Teremos que interpolar os dados para chegarmos aproximadamente na pressão desejada.

Passo 4

O método de interpolação consiste em criarmos um gráfico de reta com os dados que desejamos e assim podemos calcular a pressão.

Vai ficar mais claro, na prática!

Para 400   k P a , temos:

v = 0,53422   m 3 / k g

Para 500   k P a :

v = 0,42492   m 3 / k g

Montando o gráfico:

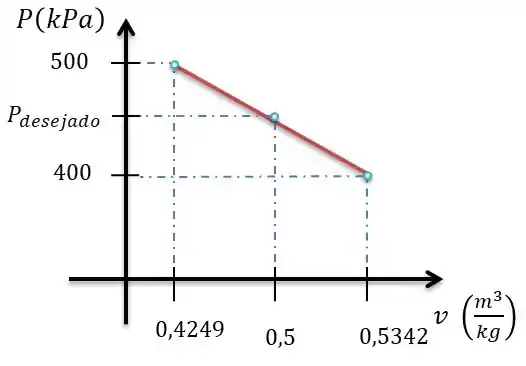
Ficou mais claro agora né! Bem como se trada de uma equação de reta, basta calcularmos a nossa pressão desejada.

Utilizarei dois pontos ( 0,5342 ; 400 ) e 0,5 ; P d e s e j a d o :

y - y 0 = m x - x 0

Substituindo:

400 - P d e s e j a d o = m 0,5342 - 0,5

O coeficiente angular pode ser determinado por:

m = y - y 0 x - x 0

Escolhendo 2 pontos que conhecemos, fica:

m = 500 - 400 0,4249 - 0,5423

Substituindo no cálculo da pressão e isolando a pressão desejada, temos:

P d e s e j a d o = - 500 - 400 0,4249 - 0,5423 ∙ 0,5342 - 0,5 + 400

P d e s e j a d o = 429,13   k P a

Resposta

P d e s e j a d o = 429,13   k P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre ∂ P / ∂ T v para gases que obedecem (a) à equação de estado de estado de Van der Waals, (b) à equação de estado aproximada do Problema 2.23 e (c) à equação de Dieterici (problema 2.30).
Deduza a equação 2-38.
a) Mostre que as constantes críticas de uma substância obedecem à equação de Dieterici de estado, P v - be a v R T = R T , são P C = a 4 e 2 b 2 ,v C = 2 b ,T C = a 4 R b b) Compare a razão P C v C /
a) Usando a relação cíclica Eq. (2-41), encontre o coeficiente de dilatação β de uma substância que obedece à equação de Dieterici de estado, dada no problema 2.30.b) A altas temperaturas e grandes vo
Usando as constantes críticas encontradas na T a b e l a2.3 , calcule o valor de b na equação de van der Waals para o C O 2 (a) a partir de v c e (b) a partir de T c e P c .