Poder Calorífico
Teoria
Fala aí! Hoje vamos aprender um pouquinho sobre poder calorífico.
Com os conceitos que veremos aqui, vamos entender por que um Fiat Uno usa etanol como combustível enquanto a NASA usa gás hidrogênio em seus foguetes. Ou por que cem gramas de batata frita 🍟 te engordam mais do que cem gramas de alface 🥬 . Tá preparado pra isso?
O que é Poder Calorífico?
O poder calorífico é a quantidade de energia que certa substância armazena.
Qual unidade a gente usa para energia? Joule ou calorias. E para quantidade de matéria? Quilogramas ou mol.
Por isso, o poder calorífico vai ser medido em algo do tipo kJ/kg ou kJ/kmol 🙂
Quanto mais energia armazenada um combustível possui, mais calor ele é capaz de liberar em sua combustão.
Dá só uma olhada na seguinte tabela com o poder calorífico de alguns dos combustíveis mais comuns:
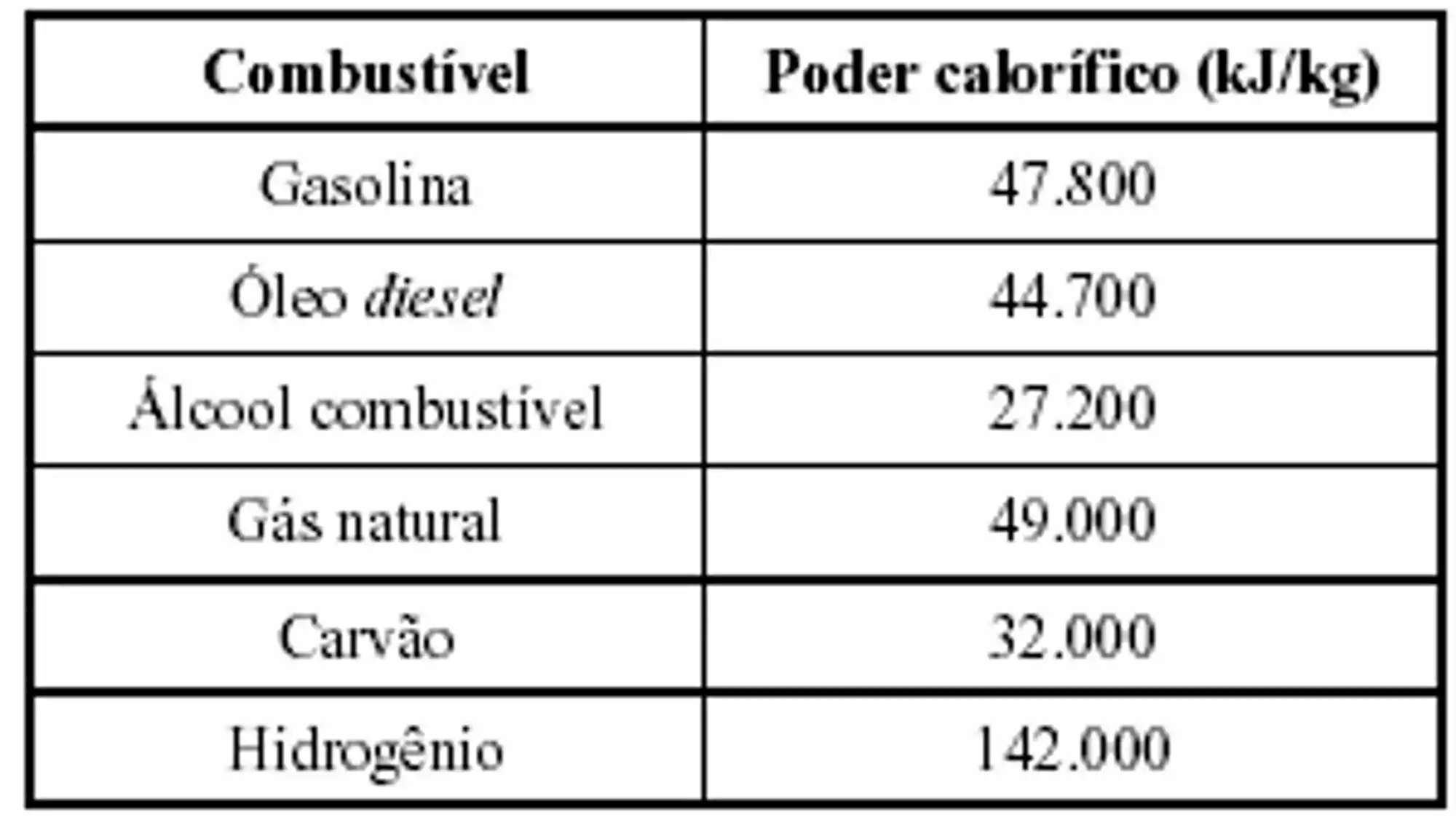
Olhando para esses valores, dá pra entender por que a NASA não abastece seus foguetes com etanol, né? A mesma massa de hidrogênio fornece cerca de 522% mais energia!
O mesmo conceito se aplica para alimentos, só que numa escala bem menor haha. Enquanto cem gramas da nossa tão amada batata frita fornece mais ou menos 310 calorias (cerca de 13 kJ/kg), cem gramas de alface fornecem míseras 15 calorias (mais ou menos 0,6 kJ/kg)!
Agora vamos ver como faz pra chegarmos nesses valores aí.
Como calcular o Poder Calorífico?
Para calcular o poder calorífico, fazemos o somatório da entalpia dos produtos de combustão vezes a vazão molar desses produtos, menos o somatório da entalpia dos reagentes vezes a vazão molar dos reagentes.
Se liga nessa fórmula do poder calorífico, pra ficar mais claro:
E o que são esse tanto de símbolo esquisito?
é o poder calorífico do combustível em base molar. A unidade no S.I. é o kJ/kmol. é a entalpia específica em base molar dos produtos que saem da câmara de combustão. A unidade é kJ/kmol. é a vazão molar dos produtos que saem da câmara de combustão. A unidade é kmol/s. é a entalpia específica em base molar dos reagentes que entram na câmara de combustão. A unidade é kJ/kmol. é a vazão molar dos reagentes que entram na câmara de combustão. A unidade é kmol/s.
E se quisermos o poder calorífico em base mássica, como foi mostrado naquela tabela lá em cima?
Podemos fazer essa conversão a partir do poder calorífico em base molar. Olha só:
é o poder calorífico do combustível em base mássica. Sua unidade no S.I. é kJ/kg. é a massa molar do combustível, medida no S.I. em kg/kmol.
Poder Calorífico Inferior (PCI) e Poder Calorífico Superior (PCS)
Quando analisamos combustíveis que têm hidrogênio em sua composição, temos que considerar a formação do vapor de água na combustão, pois isso vai levar a um gasto adicional de energia.
👉 Quando considerarmos a entalpia de formação do vapor d’água, vamos nos referir ao poder calorífico inferior.
👉 Quando considerarmos a entalpia de formação da água líquida, vamos nos referir ao poder calorífico superior.
Tranquilo? Sempre fique atento ao que o enunciado tá pedindo pra não acabar usando o valor errado! Bora ver como fica tudo isso em alguns exercícios 😉
Como calcular o Poder Calorífico?
Poder Calorífico Inferior (PCI) e Poder Calorífico Superior (PCS)
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Uma amostra de carvão é composta totalmente por carbono . Determine o poder calorífico do carvão a e em base molar.
Passo 1
O exercício pede pra gente calcular o poder calorífico em base molar a do carvão.
Determinar o poder calorífico molar de um combustível é a mesma coisa que determinar a taxa de energia que desse combustível libera por segundo ao sofrer uma combustão completa, reagindo apenas com . A equação química dessa combustão se encontra abaixo.
onde e são os coeficientes estequiométricos da combustão.
Pra encontrar esse calor liberado, vamos precisar da primeira lei da termodinâmica abaixo!
Existem dois somatórios nessa fórmula. O somatório dos reagentes e o somatório dos produtos . Os reagentes da combustão do carvão são o carbono e o oxigênio . Os produtos da combustão é o gás carbônico .
As vazões molares , e são determinadas na segunda etapa de cálculo do poder calorífico!
Passo 2
Determinar o poder calorífico molar a é a mesma coisa que determinar a quantidade de energia que desse combustível libera quando os produtos e reagentes se encontram a . Isso quer dizer que as entalpias da fórmula do poder calorífico são as entalpias a das substâncias. Logo, essas entalpias são iguais às entalpias de formação .
Como e são substâncias quimicamente mais estáveis, suas entalpias de formação valem zero!
A entalpia de formação de pode ser encontrada em uma tabela de entalpia de formação como a tabela abaixo.
Agora só falta achar as vazões molares pra encontrar ! Faremos isso no próximo passo!
Passo 3
Encontrar as vazões molares é a mesma coisa que encontrar os coeficientes estequiométricos e da equação de combustão. é a vazão molar de e é a vazão molar de . A equação de combustão se encontra abaixo.
Para determinar o poder calorífico molar , sempre consideramos que a vazão molar do combustível é de .
A vazão molar de é determinada através do balanço de carbono . Nesse balanço, os de dos produtos devem ser iguais aos de dos reagentes.
Já a vazão molar de é determinada através do balanço de oxigênio . Nesse balanço, os de dos produtos devem ser iguais aos de dos reagentes.
Com esses valores já podemos achar !
Passo 4
Vamos começar o cálculo de através da determinação dos somatórios!
O somatório das entalpias dos reagentes vale:
O somatório das entalpias dos produtos vale:
Substituindo esses valores na fórmula de :
Esses palitinhos mostram que estamos calculando o módulo do valor de dentro. Isso significa que estamos interessados no valor de dentro sem o sinal. Logo:
Boaaa! Parabééés pra gente! Fizemos nosso primeiro exercício de poder calorífico!
Resposta
Exercício Resolvido #2
Michael J. Moran, Howard N. Shapiro, Daisie D. Boettner e Margaret B. Bailey, Princípios de Termodinâmica para Engenharia, 8ª ed. Rio de Janeiro: LTC, 2018, pp. 706-13.62(a)
Determine o poder calorífico inferior, em por de combustível e em por de combustível, a , para
- etano gasoso .
Passo 1
Oi, galerinha! Vocês sabem o que é determinar o poder calorífico inferior a ?
É calcular a energia liberada pela combustão completa do combustível, quando ele reage com oxigênio puro a e gera produtos a ! O cálculo do poder calorífico inferior é feito considerando que a combustão gera apenas vapor de . A fórmula se encontar abaixo.
onde é o somatório das entalpias dos produtos. é o somatório das entalpias dos reagentes.
é o poder calorífico do combustível em por . Pra calcular o poder calorífico do combustível em por , temos que dividir pela massa molar do combustível!
Vamos iniciar as contas, calculando as vazões molares e dos produtos e reagentes!
Passo 2
Pra achar as vazões molares precisamos escrever a equação de combustão para do combustível etano .
onde , e são os coeficientes estequiométricos da combustão.
é a vazão molar de , é a vazão molar de e é a vazão molar de .
Consideramos que de está reagindo, porque é o calor liberado por unidade de combustível queimado! Logo, a vazão molar de vale:
Os outros coeficientes são encontrados, fazendo o balanço químico da equação de combustão. Ou seja, encontramos , e igualando os elementos dos reagentes aos elementos dos produtos! Em outras palavras, os de carbono dos reagentes devem ser iguais aos de dos produtos.
Além disso, o coeficiente é encontrado através do balanço de hidrogênio . Os de dos reagentes devem ser iguais aos de dos produtos.
Por fim, achamos o coeficiente por meio do balanço de . A equação desse balanço se encontra abaixo.
Uhuuul! Achamos as vazões molares! Agora só falta achar as entalpias pra calcular os somatórios e o poder calorífico!
Passo 3
As entalpias precisam ser encontradas pra gente poder encontrar os valores dos somatórios!
A entalpia das substâncias é a soma entre a entalpia de formação e a diferença de entalpia .
é a diferença entre a entalpia da substância e a entalpia que ela teria caso estivesse a . Como os reagentes e produtos se encontram a nessa combustão, os dos reagentes e produtos valem zero. Logo todas as entalpias são iguais às entalpias de formação.
A entalpia de formação do vale zero, porque é uma substância quimicamente mais estável. A entalpia de formação do e de pode ser encontrada na tabela de entalpias de formação. Mas atenção! Devemos pegar a entalpia de formação do vapor d’água, porque o enunciado quer o poder calorífico inferior da combustão !
Com esses dados em mãos, podemos determinar os valores dos somatórios de entalpias!
Passo 4
O somatório das entalpias dos reagentes é:
Já o somatório das entalpias dos produtos vale:
Substituindo esse valores na equação de :
Os tracinhos ao lado indicam que temos que calcular o módulo. Ou seja, esses tracinhos indicam que queremos saber o valor que está dentro! Sem o sinal!
Como é o calor liberado por de combustível queimado, a unidade do é .
Como a massa molar do combustível vale , vale:
Ebaaaaaa! Calculamos os dois valores! Mandamos muito!
Resposta
Exercício Resolvido #3
Michael J. Moran, Howard N. Shapiro, Daisie D. Boettner e Margaret B. Bailey, Princípios de Termodinâmica para Engenharia, 8ª ed. Rio de Janeiro: LTC, 2018, pp. 706-13.62(b)
Determine o poder calorífico inferior, em por de combustível e em por de combustível, a , para
- etanol líquido .
Passo 1
Oi, galerinha! Vocês sabem o que é determinar o poder calorífico inferior a ?
É calcular a energia liberada pela combustão completa do combustível, quando ele reage com oxigênio puro a e gera produtos a ! O cálculo do poder calorífico inferior é feito considerando que a combustão gera apenas vapor de . A fórmula se encontar abaixo.
onde é o somatório das entalpias dos produtos. é o somatório das entalpias dos reagentes.
é o poder calorífico do combustível em por . Pra calcular o poder calorífico do combustível em por , temos que dividir pela massa molar do combustível!
Vamos iniciar as contas, calculando as vazões molares e dos produtos e reagentes!
Passo 2
Pra achar as vazões molares precisamos escrever a equação de combustão para do combustível etano .
onde , e são os coeficientes estequiométricos da combustão.
é a vazão molar de , é a vazão molar de e é a vazão molar de .
Consideramos que de está reagindo, porque é o calor liberado por unidade de combustível queimado! Logo, a vazão molar de vale:
Os outros coeficientes são encontrados, fazendo o balanço químico da equação de combustão. Ou seja, encontramos , e igualando os elementos dos reagentes aos elementos dos produtos! Em outras palavras, os de carbono dos reagentes devem ser iguais aos de dos produtos.
Além disso, o coeficiente é encontrado através do balanço de hidrogênio . Os de dos reagentes devem ser iguais aos de dos produtos.
Por fim, achamos o coeficiente por meio do balanço de . A equação desse balanço se encontra abaixo.
Uhuuul! Achamos as vazões molares! Agora só falta achar as entalpias pra calcular os somatórios e o poder calorífico!
Passo 3
As entalpias precisam ser encontradas pra gente poder encontrar os valores dos somatórios!
A entalpia das substâncias é a soma entre a entalpia de formação e a diferença de entalpia .
é a diferença entre a entalpia da substância e a entalpia que ela teria caso estivesse a . Como os reagentes e produtos se encontram a nessa combustão, os dos reagentes e produtos valem zero. Logo todas as entalpias são iguais às entalpias de formação.
A entalpia de formação do vale zero, porque é uma substância quimicamente mais estável. A entalpia de formação do e de pode ser encontrada na tabela de entalpias de formação. Mas atenção! Devemos pegar a entalpia de formação do vapor d’água, porque o enunciado quer o poder calorífico inferior da combustão !
Com esses dados em mãos, podemos determinar os valores dos somatórios de entalpias!
Passo 4
O somatório das entalpias dos reagentes é:
Já o somatório das entalpias dos produtos vale:
Substituindo esse valores na equação de :
Os tracinhos ao lado indicam que temos que calcular o módulo. Ou seja, esses tracinhos indicam que queremos saber o valor que está dentro! Sem o sinal!
Como é o calor liberado por de combustível queimado, a unidade do é .
Como a massa molar do combustível vale , vale:
Ebaaaaaa! Calculamos os dois valores! Mandamos muito!
Resposta
Exercício Resolvido #4
Elaboração própria
Determine a entalpia de formação do fenol , sabendo que o poder calorífico inferior do fenol vale .
Passo 1
Fala, pessoal! Perceberam que esse exercício é invertido? Geralmente, conhecemos as entalpias de formação e a questão pede o poder calorífico do combustível. No entanto, esse exercício faz o contrário! Ele nos dá o poder calorífico da combustão do e pede a entalpia de formação do . Para calcular , usaremos a primeira lei abaixo.
é a taxa de calor trocada. é a taxa de trabalho realizada. é a vazão molar dos reagentes e é a vazão molar dos produtos.
Como o poder calorífico inferior é o calor liberado pela queima de combustível, a taxa de calor trocada é igual a com um sinal de menos na frente!
Além disso, o exercício não fala nada sobre realização de trabalho durante a combustão. Por isso, a taxa de trabalho vale zero!
Já conhecemos dois valores da primeira lei. No entanto, precisamos aprender a calcular os somatórios. Pra achar a entalpia de formação do que queremos!
Passo 2
Para calcular os somatórios, precisamos saber o valor das vazões molares dos reagentes e dos produtos . Descobrimos isso, escrevendo a equação de combustão completa de reagindo com puro.
onde , e são os coeficientes estequiométricos da combustão.
é a vazão molar de , é a vazão molar de e é a vazão molar de .
Consideramos que de está reagindo, porque é o calor liberado por unidade de combustível queimado! Logo, a vazão molar de vale:
Os outros coeficientes são encontrados, fazendo o balanço químico da equação de combustão. Ou seja, encontramos , e igualando os elementos dos reagentes aos elementos dos produtos! Em outras palavras, os de carbono dos reagentes devem ser iguais aos de dos produtos.
Além disso, o coeficiente é encontrado através do balanço de hidrogênio . Os de dos reagentes devem ser iguais aos de dos produtos.
Por fim, achamos o coeficiente por meio do balanço de . A equação desse balanço se encontra abaixo.
Com esses valores, somos capazes de achar os somatórios e e de calcular do fenol.
Passo 3
O somatório dos reagentes é a soma das entalpias dos reagentes e .
A entalpia de formação do vale zero, porque é uma substância quimicamente mais estável. Além disso, os dos reagentes valem zero, porque eles estão a . Substituindo
essas informações no cálculo do somatório dos reagentes:
No próximo passo descobrimos quanto vale o somatório dos produtos!
Passo 4
O somatório dos reagentes é a soma das entalpias dos produtos e .
A entalpia de formação do e de pode ser encontrada na tabela de entalpias de formação. Mas atenção! Devemos pegar a entalpia de formação do vapor d’água, porque o enunciado quer o poder calorífico inferior da combustão !
Além disso, os dos produtos valem zero, porque eles estão a . Substituindo
essas informações no cálculo do somatório dos produtos:
Agora podemos substituir os valores na primeira lei e achar a entalpia de formação!
Passo 5
Sem enrolação, vamos substituir direto os resultados das nossas contas na equação da primeira lei!
Uhuuuuul! Arrasamos! Encontramos o resultado que o enunciado pediu!
Resposta
Exercício Resolvido #5
Elaboração própria
Determine o poder calorífico inferior, em por de combustível e em por de combustível, a , para propano gasoso . Suponha que o calor específico médio a pressão constante do propano entre e é igual a .
Passo 1
Oi, galerinha! Vocês sabem o que é determinar o poder calorífico inferior a ?
É calcular a energia liberada pela combustão completa do combustível, quando ele reage com oxigênio puro a e gera produtos a ! O cálculo do poder calorífico inferior é feito considerando que a combustão gera apenas vapor de . A fórmula se encontar abaixo.
onde é o somatório das entalpias dos produtos. é o somatório das entalpias dos reagentes.
é o poder calorífico do combustível em por . Pra calcular o poder calorífico do combustível em por , temos que dividir pela massa molar do combustível!
Vamos iniciar as contas, calculando as vazões molares e dos produtos e reagentes!
Passo 2
Pra achar as vazões molares precisamos escrever a equação de combustão para do combustível etano .
onde , e são os coeficientes estequiométricos da combustão.
é a vazão molar de , é a vazão molar de e é a vazão molar de .
Consideramos que de está reagindo, porque é o calor liberado por unidade de combustível queimado! Logo, a vazão molar de vale:
Os outros coeficientes são encontrados, fazendo o balanço químico da equação de combustão. Ou seja, encontramos , e igualando os elementos dos reagentes aos elementos dos produtos! Em outras palavras, os de carbono dos reagentes devem ser iguais aos de dos produtos.
Além disso, o coeficiente é encontrado através do balanço de hidrogênio . Os de dos reagentes devem ser iguais aos de dos produtos.
Por fim, achamos o coeficiente por meio do balanço de . A equação desse balanço se encontra abaixo.
Uhuuul! Achamos as vazões molares! Agora só falta achar as entalpias pra calcular os somatórios e o poder calorífico!
Passo 3
As entalpias precisam ser encontradas pra gente poder encontrar os valores dos somatórios!
A entalpia das substâncias é a soma entre a entalpia de formação e a diferença de entalpia .
A entalpia de formação do vale zero, porque é uma substância quimicamente mais estável. A entalpia de formação do , de e do pode ser encontrada na tabela de entalpias de formação. Mas atenção! Devemos pegar a entalpia de formação do vapor d’água, porque o enunciado quer o poder calorífico inferior da combustão !
Agora só falta encontrar os valores de de , , e pra poder calcular os somatórios de entalpia!
Passo 4
de , e é encontrado em tabelas como as tabelas abaixo.
Já conseguimos os valores de quase todas as diferenças de entalpia por tabelas. No entanto, o de geralmente não está disponível em tabelas! Precisamos calcular o de que está em estado gasoso através da fórmula de gás perfeito que usa o calor específico médio .
é a massa molar do que vale . é a diferença de temperatura .
Substituindo esses valores:
Com esses dados em mãos, podemos determinar os valores dos somatórios de entalpias!
Passo 5
O somatório das entalpias dos reagentes é:
Já o somatório das entalpias dos produtos vale:
Substituindo esse valores na equação de :
Os tracinhos ao lado indicam que temos que calcular o módulo. Ou seja, esses tracinhos indicam que queremos saber o valor que está dentro! Sem o sinal!
Como é o calor liberado por de combustível queimado, a unidade do é .
Como a massa molar do combustível vale , vale:
Ebaaaaaa! Calculamos os dois valores! Mandamos muito!
Resposta
Exercício Resolvido #6
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 484-14.58
O gás combustível, produzido num fermentador de biomassa, apresenta a seguinte composição (em base molar): de metano, de dióxido de carbono e de hidrogênio. Determine o poder calorífico inferior deste gás combustível por unidade de volume.
Passo 1
Oi, galerinha! Vocês sabem o que é determinar o poder calorífico inferior?
É calcular a energia liberada pela combustão completa do combustível, quando ele reage com oxigênio puro a e gera produtos a ! O cálculo do poder calorífico inferior é feito considerando que a combustão gera apenas vapor de . A fórmula se encontar abaixo.
onde é o somatório das entalpias dos produtos. é o somatório das entalpias dos reagentes.
é o poder calorífico do combustível em por . Pra calcular o poder calorífico do combustível por unidade de volume (em por ), usamos a equação de gás perfeito abaixo.
onde é a pressão do gás combustível que vale (pressão atmosférica aproximada) pro cálculo de . é a constante universal do gás ideal que vale . é a temperatura de do gás em kelvin . Multiplicando por , achamos o poder calorífico do gás por unidade de volume.
Vamos iniciar as contas, calculando as vazões molares e dos produtos e reagentes!
Passo 2
Pra achar as vazões molares, precisamos escrever a equação de combustão para uma vazão molar total de do gás combustível composto de , e .
Consideramos que de gás está reagindo, porque é o calor liberado por unidade de combustível queimado!
onde , , , , e são os coeficientes estequiométricos da combustão.
é a vazão molar de , é a vazão molar de , é a vazão molar de , é a vazão molar de , é a vazão molar de e é a vazão molar de . Pra achar a vazão molar de precisamos multiplicar a vazão total de pelos de do combustível!
Usamos o mesmo método pra determinar a vazão de dos reagentes. Multiplicamos a vazão total de de gás combustível pela porcentagem de presente no gás.
Por fim, achamos a vazão de do mesmo jeito! Multiplicamos a vazão total de gás combustível pela porcentagem de presente no gás.
Os outros coeficientes são encontrados, fazendo o balanço químico da equação de combustão.
Faremos o balanço no próximo passo!
Passo 3
Encontramos , através do balanço de carbono . Os de carbono dos reagentes devem ser iguais aos de dos produtos.
Além disso, o coeficiente é encontrado através do balanço de hidrogênio . Os de dos reagentes devem ser iguais aos de dos produtos.
Por fim, achamos o coeficiente por meio do balanço de . A equação desse balanço se encontra abaixo.
Uhuuul! Achamos as vazões molares! Agora só falta achar as entalpias pra calcular os somatórios e o poder calorífico!
Passo 4
As entalpias precisam ser encontradas pra gente poder encontrar os valores dos somatórios!
A entalpia das substâncias é a soma entre a entalpia de formação e a diferença de entalpia .
é a diferença entre a entalpia da substância e a entalpia que ela teria caso estivesse a . Como os reagentes e produtos se encontram a nessa combustão, os dos reagentes e produtos valem zero. Logo todas as entalpias são iguais às entalpias de formação.
A entalpia de formação de e vale zero, porque os dois são substâncias quimicamente mais estáveis. A entalpia de formação do , de e do pode ser encontrada na tabela de entalpias de formação. Mas atenção! Devemos pegar a entalpia de formação do vapor d’água, porque o enunciado quer o poder calorífico inferior da combustão !
Com esses dados em mãos, podemos determinar os valores dos somatórios de entalpias!
Passo 5
O somatório das entalpias dos reagentes é:
Já o somatório das entalpias dos produtos vale:
Substituindo esse valores na equação de :
Os tracinhos ao lado indicam que temos que calcular o módulo. Ou seja, esses tracinhos indicam que queremos saber o valor que está dentro! Sem o sinal!
Como é o calor liberado por de combustível queimado, a unidade do é .
Agora, vamos descobrir quanto nave do gás combustível pra poder converter o poder calorífico de pra .
Lembrando, é a pressão do gás combustível que vale (pressão atmosférica aproximada). é a constante universal do gás ideal que vale . é a temperatura de do gás em kelvin . Substituindo esses dados:
Multiplciando por :
Uhuuuuuul! Mandamos muito!
Resposta
Exercício Resolvido #7
Elaboração própria
Uma mistura gasosa de n-butano e metanol apresenta análise em massa de de n-butano e de metanol . Determine o poder calorífico superior da mistura combustível em por .
Passo 1
Faaala, pessoal! Diz aí: vocês sabem o que é determinar o poder calorífico superior?
É calcular a energia liberada pela combustão completa do combustível, quando ele reage com oxigênio puro a e gera produtos a ! O cálculo do poder calorífico superior é feito considerando que a combustão gera apenas líquido. A fórmula se encontar abaixo.
onde é o somatório das entalpias dos produtos. é o somatório das entalpias dos reagentes.
é o poder calorífico do combustível em por . Nós podemos calcular direto, porque a composição do combustível foi dada em base mássica (porcentagem de massa)!
Como a gente não vai precisar calcular o poder calorífico superior em por primeiro pra só depois achar , nosso trabalho vai ficar muito menor!
Vamos iniciar as contas, calculando as vazões molares e dos produtos e reagentes!
Passo 2
Pra achar as vazões molares, precisamos escrever a equação de combustão para uma vazão mássica total de do gás combustível composto de , .
Consideramos que de gás está reagindo, porque a composição da mistura combustível é dada em porcentagens de massa! Veremos como essa escolha vai facilitar nossa vida!
onde , , , e são os coeficientes estequiométricos da combustão.
é a vazão molar de , é a vazão molar de , é a vazão molar de , é a vazão molar de e é a vazão molar de . Pra achar a vazão molar de , achamos a vazão mássica de , multiplicando pelos de do combustível!
Dividindo esse valor pela massa molar de , que vale , encontramos a vazão molar de !
Usamos o mesmo método pra determinar a vazão de . Primeiro, achamos a vazão mássica , multiplicando a vazão total de de combustível pela porcentagem de presente no gás.
Depois, dividimos essa vazão mássica pela massa molar pra achar o valor da vazão molar de . vale .
Os outros coeficientes são encontrados, fazendo o balanço químico da equação de combustão.
Faremos o balanço no próximo passo!
Passo 3
Encontramos o coeficiente , através do balanço de carbono . Os de carbono dos reagentes devem ser iguais aos de dos produtos.
Além disso, o coeficiente é encontrado através do balanço de hidrogênio . Os de dos reagentes devem ser iguais aos de dos produtos.
Por fim, achamos o coeficiente por meio do balanço de . A equação desse balanço se encontra abaixo.
Uhuuul! Achamos as vazões molares! Agora só falta achar as entalpias pra calcular os somatórios e o poder calorífico!
Passo 4
As entalpias precisam ser encontradas pra gente poder encontrar os valores dos somatórios!
A entalpia das substâncias é a soma entre a entalpia de formação e a diferença de entalpia .
é a diferença entre a entalpia da substância e a entalpia que ela teria caso estivesse a . Como os reagentes e produtos se encontram a nessa combustão, os dos reagentes e produtos valem zero. Logo todas as entalpias são iguais às entalpias de formação.
A entalpia de formação de vale zero, porque ele é uma substância quimicamente mais estável. A entalpia de formação do , de , de e pode ser encontrada na tabela de entalpias de formação. Mas atenção! Devemos pegar a entalpia de formação da água líquida, porque o enunciado quer o poder calorífico superior da combustão !
Com esses dados em mãos, podemos determinar os valores dos somatórios de entalpias!
Passo 5
O somatório das entalpias dos reagentes é:
Já o somatório das entalpias dos produtos vale:
Substituindo esse valores na equação de :
Os tracinhos ao lado indicam que temos que calcular o módulo. Ou seja, esses tracinhos indicam que queremos saber o valor que está dentro! Sem o sinal!
Como é o calor liberado por de combustível queimado, a unidade do é .
Booooa, pessoal! Calculamos o que o enunciado nos pediu!
Resposta
Exercício Resolvido #8
Elaboração própria
Uma amostra seca de carvão apresenta a seguinte análise mássica de: de carbono , de hidrogênio , de oxigênio , de nitrogênio , de enxofre e o restante de cinzas não combustíveis.
Determine o poder calorífico superior da mistura combustível em por .
Passo 1
Faaala, pessoal! Diz aí: vocês sabem o que é determinar o poder calorífico superior?
É calcular a energia liberada pela combustão completa do combustível, quando ele reage com oxigênio puro a e gera produtos a ! O cálculo do poder calorífico superior é feito considerando que a combustão gera apenas líquido. A fórmula se encontar abaixo.
onde é o somatório das entalpias dos produtos. é o somatório das entalpias dos reagentes.
é o poder calorífico do combustível em por . Nós podemos calcular direto, porque a composição do combustível foi dada em base mássica (porcentagem de massa)!
Vamos iniciar as contas, calculando as vazões molares e dos produtos e reagentes!
Passo 2
Pra achar as vazões molares, precisamos escrever a equação de combustão para uma vazão mássica total de do gás combustível composto de , , , e .
Consideramos que de gás está reagindo, porque a composição da mistura combustível é dada em porcentagens de massa! Veremos como essa escolha vai facilitar nossa vida!
onde , , , , , , , , e são os coeficientes estequiométricos da combustão.
Esses coeficientes são as vazões molares das substâncias. Por exemplo, é a vazão molar de e é a vazão molar de . Pra achar a vazão molar de , achamos a vazão mássica de , multiplicando a vazão total de de combustível pelos de do combustível!
Dividindo esse valor pela massa molar de , que vale , encontramos a vazão molar de !
Usamos o mesmo método pra determinar a vazão de . Primeiro, achamos a vazão mássica , multiplicando a vazão total de de combustível pela porcentagem de presente no combustível.
Depois, dividimos essa vazão mássica pela massa molar pra achar o valor da vazão molar de . vale .
Vamos usar o mesmo passo a passo pra achar as vazões molares , e de , e . Novamente multiplicamos as porcentagens pela vazão total de pra achar as vazões mássicas. Por fim, dividimos as vazões mássicas pelas massas molares pra achar as vazões molares! Começamos pelo que representa do carvão.
Dividindo essa vazão pela massa molar , achamos o coeficiente .
O representa do combustível. Logo:
Dividindo essa vazão pela massa molar , achamos o coeficiente .
Por fim, achamos o coeficiente que é a vazão molar de . representa do combustível.
Dividindo essa vazão pela massa molar , achamos o coeficiente .
Os outros coeficientes são encontrados, fazendo o balanço químico da equação de combustão.
Faremos o balanço no próximo passo!
Passo 3
Encontramos o coeficiente , através do balanço de carbono . Os de carbono dos reagentes devem ser iguais aos de dos produtos.
Além disso, o coeficiente é encontrado através do balanço de hidrogênio . Os de dos reagentes devem ser iguais aos de dos produtos.
Encontramos o coeficiente de por meio do balanço de . Os de dos reagentes devem ser iguais aos de dos produtos.
O coeficiente é determinado pelo balanço de . Os de dos reagentes devem ser iguais aos de dos produtos.
Por fim, achamos o coeficiente por meio do balanço de . A equação desse balanço se encontra abaixo.
Uhuuul! Achamos as vazões molares! Agora só falta achar as entalpias pra calcular os somatórios e o poder calorífico!
Passo 4
As entalpias precisam ser encontradas pra gente poder encontrar os valores dos somatórios!
A entalpia das substâncias é a soma entre a entalpia de formação e a diferença de entalpia .
é a diferença entre a entalpia da substância e a entalpia que ela teria caso estivesse a . Como os reagentes e produtos se encontram a nessa combustão, os dos reagentes e produtos valem zero. Logo todas as entalpias são iguais às entalpias de formação.
A entalpia de formação de , , , e valem zero, porque eles são substâncias quimicamente mais estáveis.
A entalpia de formação do , de e pode ser encontrada na tabela de entalpias de formação. Mas atenção! Devemos pegar a entalpia de formação da água líquida, porque o enunciado quer o poder calorífico superior da combustão !
Com esses dados em mãos, podemos determinar os valores dos somatórios de entalpias!
Passo 5
O somatório das entalpias dos reagentes é:
Já o somatório das entalpias dos produtos vale:
Substituindo esse valores na equação de :
Os tracinhos ao lado indicam que temos que calcular o módulo. Ou seja, esses tracinhos indicam que queremos saber o valor que está dentro! Sem o sinal!
Como é o calor liberado por de combustível queimado, a unidade do é .
Shoe de bola, pessoal! Calculamos o que o enunciado nos pediu!