Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Terceira Lei da Termodinâmica

Ver Todos os Exercícios

Teoria

Opaa! Bora conversar sobre a Terceira Lei da Termodinâmica?!

O que diz a 3º Lei da Termodinâmica?

O enunciado da Terceira Lei da Termodinâmica é essa daqui:

A variação da entropia de qualquer transformação física ou química tende a zero quando a temperatura tende a zero, admitindo-se que todas as substâncias envolvidas estão perfeitamente ordenadas.”

-Beleza…mas o que isso significa? 😖

O negócio é o seguinte, no zero absoluto todas as partículas do sistema estão paradinha, não tem nenhuma vibração! A entropia diz pra o grau de desordem de um sistema e tem sistema mais organizado do que um sistema completamente estático?! Ou seja:

A medida que a temperatura se aproxima de zero, a entropia também se aproxima de zero!

-Beleza, mas e daí? O que isso muda?

Muita coisa, meu caro…muita coisa! Pra entender melhor quais são as implicações da 3ª lei da termodinâmica, dá uma conferida nesse vídeo abaixo que o Responde Aí preparou pra você! 🧡

Entropia

A entropia de um sistema esta relacionado a quantas formas diferentes a gente pode organizar um sistema. Por exemplo, se liga nesse pote aqui em baixo:

Sistema
Sistema

Você concorda comigo que existem MUITAS formas de organizar esse sistema?! Agora imagina que eu abro esse pote e esparramo todas as bolinhas pelo chão da sala. Concorda comigo que nesse novo cenário existem mais formas de organizar o sistema?

Isso significa que a entropia aumentou, o que faz muito sentido afinal a entropia do universo sempre aumenta!

Entropia Absoluta

O valor de entropia medido usando um cristal a zero kelvin como referência é chamado de entropia absoluta. Mas atenção! As entropias informadas em tabelas termodinâmicas de vapor, líquido e mistura saturada não são entropias absolutas!

Elas não consideram que a entropia do cristal a 0 K vale zero e não calculam a entropia a partir da entropia do cristal:

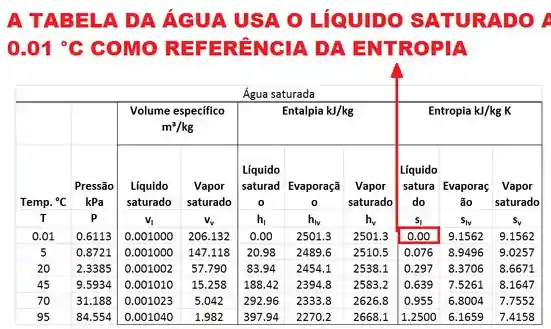
Tabela de entropia
Tabela de entropia

Geralmente, as tabelas de entropia absoluta que temos só nos mostram a entropia absoluta por kmol de gases perfeitos. Essas tabelas possuem os valores das entropias por kmol para várias temperaturas. No entanto, todos esses valores são calculados para uma única pressão de 0,1 MPa. Use essas tabelas em exercícios que envolvem reação química! Como podemos ver na tabela abaixo:

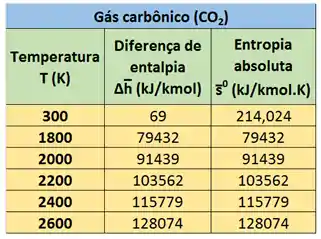
Tabela de entropia absoluta
Tabela de entropia absoluta

Agora vamos praticar com exercícios?

Entropia

Exercícios Resolvidos

Exercício Resolvido #1

Elaboração própria

Determine a entropia absoluta da água líquida que se encontra a 25   ° C e 100   k P a .

Passo 1

O exercício pede pra gente descobrir o valor de entropia absoluta s - 0 da água líquida que tem uma temperatura de 25   ° C e pressão de 100   k P a ! Tome muito cuidado para NÃO pegar o valor de entropia da água líquida presente na tabela de propriedades da água mostrada abaixo.

Esse valor de entropia 0,3673   k J / k g K são é o valor da entropia absoluta!

Gerlmente, os valores de entropia absoluta s - 0 de uma substância que se encontra a 25   ° C e 100   k P a estão na mesma tabela que os valores de entalpia de formação h - f 0 .

Agora que sabemos qual tabela usar, vamos obter o valor de entropia absoluta que queremos da tabela.

Passo 2

Tenha atenção na hora de pegar o valor de entropia absoluta da água, porque a água tem dois valores de entropia absoluta. Um para vapor d’água e gás de água e outro pra água líquida!

Como o enunciado pedir o valor da entropia absoluta da água líquida, pegaremos o valor da água líquida!

A tabela mostra que a entropia absoluta da água líquida a 25   ° C e 100   k P a vale:

s - 0 = 69,950   k J / k m o l

Uhuuuuul! Achamos a resposta!! Bate aqui!

Resposta

s - 0 = 69,950   k J / k m o l

Exercício Resolvido #2

Elaboração própria

Um tanque rígido possui 3   k m o l de hidrogênio H 2 a uma temperatura de 226,85   ° C e a uma pressão de 0,1   M P a . Determine a entropia absoluta total do gás hidrogênio no tanque.

Passo 1

O exercício pede pra gente descobrir o valor de entropia absoluta S do H 2 que tem uma temperatura de 226,85   ° C e pressão de 100   k P a !

A entropia absoluta S de H 2 é igual à entropia absoluta por unidade de k m o l s - vezes a quantidade n de k m o l de H 2 .

S = n × s -

A quantidade n de k m o l de H 2 é igual a 3   k m o l . Como H 2 pode ser considerado um gás perfeito, podemos encontrar o valor de entropia absoluta por k m o l s - para temperaturas diferentes de 25   ° C em uma tabela parecida com a tabela abaixo.

Agora que já conhecemos a tabela de entropia absoluta por unidade de k m o l , podemos encontrar o valor que precisamos!

Passo 2

Como podemos, ver a tabela possui valores de entropia para temperaturas em kelvin K . Por isso, antes de tudo devemos converter a temperatura em ° C que temos pra K , somando ela com 273,15 .

T = 226,85 + 273,15

T = 500   K

Agora é só encontar a entropia pra H 2 a 500   K !

s - = 125,463   k J k m o l K

Substituindo esse valor na fórmula da entropia S :

S = n × s -

S = 3 × 125,463  

S = 376,389 k J K

Booooaaa! Achamos o valor da entropia absoluta que a questão pediu!!

Resposta

S = 376,389 k J K

Exercício Resolvido #3

Elaboração própria

Determine a entropia absoluta em base mássica do gás hidrogênio H 2 que se encontra a 200   ° C e a 0,1   M P a .

Passo 1

Fala, gente! Esse exercício pede o valor de entropia absoluta em base mássica s do H 2 que tem uma temperatura de 200   ° C e pressão de 0,1   M P a ! Isso é a mesma coisa que pedir pra gente o valor da entropia por unidade de massa! O problema é só temos tabelas que informam o valor da entropia por unidade de k m o l s - . Logo, precisamos converter s - pela fórmula abaixo!

s = s - M

onde M é a massa molar da substância. Como a substância é o H 2 , a massa molar vale:

M = 2,016   k g k m o l

Esse valor é geralmente encontrado em tabelas de gases perfeitos.

Como H 2 pode ser considerado um gás perfeito, podemos encontrar o valor de entropia absoluta por k m o l s - para temperaturas diferentes de 25   ° C em uma tabela parecida com a tabela abaixo.

Agora que já conhecemos a tabela de entropia absoluta por unidade de k m o l , podemos encontrar o valor que precisamos!

Passo 2

Como podemos, ver a tabela possui valores de entropia para temperaturas em kelvin K . Por isso, antes de tudo devemos converter a temperatura em ° C que temos pra K , somando ela com 273,15 .

T = 200 + 273,15

T = 473,15   K

Agora é só encontar a entropia pra H 2 a 473,15   K ! Mas olha que tragédia! Não existe valor de entropia s - para a temperatura de 473,15   K ! Só existe o valor de entropia pra uma temperatura menor de 400   K e outro valor de entropia pra uma temperatura maior de 500   K ! O valor que queremos está entre essas duas temperaturas. Logo, vamos interpolar a tabela!

s - = 120,825 + 125,463 - 120,825 500 - 400 × 473,15 - 400

s - = 124,22   k J k m o l K

Que show! Achamos o valor interpolado de s - !

Substituindo esse valor na fórmula da entropia por unidade de massa s :

s = s - M

s = 124,22 2,016

s = 61 , 617 k J k g

Que iiiiiissso!! Tá ficando craque em cálculo de entropia absoluta, heim?

Resposta

s = 61 , 617 k J k g

Exercício Resolvido #4

Elaboração própria

Determine a entropia absoluta em base mássica do gás carbônico C O 2 que se encontra a 350   ° C e a 0,5   M P a .

Passo 1

Oi, galera! Esse exercício pede o valor de entropia absoluta em base mássica s do C O 2 que tem uma temperatura de 350   ° C e pressão de 0,5   M P a ! Isso é a mesma coisa que pedir pra gente o valor da entropia por unidade de massa! O problema é só temos tabelas que informam o valor da entropia por unidade de k m o l s - . Logo, precisamos converter s - pela fórmula abaixo!

s = s - M

onde M é a massa molar da substância. Como a substância é o C O 2 , a massa molar vale 44,01   k g / k m o l segundo tabelas de gases perfeitos.

Mas temos outro problema! A tabela que temos só serve para gases a 0,1   M P a de pressão! O exercício quer o valor de entropia pra pressão de 0,5   M P a ! Por isso, usamos a fórmula abaixo!

s - = s - T 0 - R - × ln ⁡ P P 0

onde:

  • s - é a entropia absoluta por k m o l a temperatura T = 350   ° C que queremos e a pressão P = 0,5   M P a que queremos;

  • R - é a constante universal dos gases. Seu valor é igual para todos os gases e se encontra abaixo.

    • R - = 8,314   k J k m o l × K

  • s - T é a entropia absoluta por k m o l que está na tabela. Ela é a entropia para a temperatura T = 350   ° C que queremos, mas para a pressão 0,1   M P a da tabela;

  • P 0 é a pressão de tabela em que pegamos o valor da entropia absoluta. No caso, a pressão das tabelas que temos valem 0,1   M P a .

Como C O 2 pode ser considerado um gás perfeito, podemos encontrar o valor de entropia absoluta por k m o l s - T para temperaturas diferentes de 25   ° C e prassão de 0,1   M P a em uma tabela. Faremos isso no próximo passo!

Passo 2

Recaptulando, vamos resolver o exercício pegando o valor de entropia absoluta s - T do C O 2 a T = 350   ° C e P 0 = 0,1   M P a . Depois, vamos usar uma fórmula pra achar a entropia absoluta por k m o l s - do C O 2 a T = 350   ° C e P = 0,5   M P a . Por fim, convertermos essa entropia s - pra entropia por unidade de massa s através de outra fórmula!

A tabela de s - T pro C O 2 se encontra abaixo.

Como podemos, ver a tabela possui valores de entropia para temperaturas em kelvin K . Por isso, antes de tudo devemos converter a temperatura em ° C que temos pra K , somando ela com 273,15 .

T = 350 + 273,15

T = 623,15   K

Agora é só encontar a entropia pra C O 2 a 623,15   K ! Mas olha que tragédia! Não existe valor de entropia s - T para a temperatura de 623,15   K ! Só existe o valor de entropia pra uma temperatura menor de 600   K e outro valor de entropia pra uma temperatura maior de 700   K ! O valor que queremos está entre essas duas temperaturas. Logo, vamos interpolar a tabela!

s - T = 243,284 + 2 50,752 - 243,284 700 - 600 × 623,15 - 600

s - T = 245,013   k J k m o l K

Que show! Achamos o valor interpolado de s - T ! Agora só falta achar s - e s no próximo passo.

Passo 3

Primeiro, convertemos o valor s - T do C O 2 a 623,15   K e 0,1   M P a pro valor s - do C O 2 a 623,15   K e 0,5   M P a .

s - = s - T 0 - R - × ln ⁡ P P 0

s - = 245,013 - 8,314 × ln ⁡ 0,5 0,1

s - = 231 , 6321   k J k m o l K

Substituindo esse valor na fórmula da entropia por unidade de massa s :

s = s - M

s = 231 , 6321 44,01

s = 5 , 263 k J k g

Shoooow de boooola! Mais um exercício pra conta, maninh@!

Resposta

s = 5 , 263 k J k g

Exercício Resolvido #5

Elaboração própria

Determine a entropia absoluta em base mássica do gás carbônico C O 2 que se encontra a 220   ° C e a 0,1   M P a , usando apenas a tabela entropia absoluta das substâncias a 25   ° C e 0,1   M P a .

Passo 1

Oi, galera! Esse exercício pede o valor de entropia absoluta em base mássica s do C O 2 que tem uma temperatura de 220   ° C e pressão de 0,1   M P a ! Isso é a mesma coisa que pedir pra gente o valor da entropia por unidade de massa! O problema é só temos tabelas que informam o valor da entropia por unidade de k m o l s - . Logo, precisamos converter s - pela fórmula abaixo!

s = s - M

onde M é a massa molar da substância. Como a substância é o C O 2 , a massa molar vale 44,01   k g / k m o l segundo tabelas de gases perfeitos.

No entanto, o exercício só permitiu a gente de usar a tabela abaixo que possui a entropia absoluta s - 0 das substâncias a 25   ° C e a 0,1   M P a .

Ou seja, nós precisamos achar o valor da entropia absoluta por k m o l s - do C O 2 a 220   ° C e 0,1   M P a , mas nós só podemos usar uma tabela que nos dá o valor da entropia absoluta por k m o l s - 0 do C O 2 a 25   ° C 298,15   K e 0,1   M P a . Existe um macetão pra fazer s - 0 virar s - . Através da a equação abaixo, achamos s - a partir de s - 0 !

s - = s - 0 + c - p 0 × ln ⁡ T T 0

onde T é a temperatura em kelvin do C O 2 e T 0 é a temperatura de 298,15   K . c - p 0 é o calor específico a pressão constante em k J / k m o l K .

No próximo passo, veremos como pegar o valor s - 0 da tabela e como chegar na entropia absoluta s .

Passo 2

O valor de s - 0 se encontra abaixo.

s - 0 = 213,795   k J k m o l K

Substituímos a equação de s - na fórmula de s e encontramos:

s = s - M

s = s - 0 + c - p 0 × ln ⁡ T T 0 M

s = s - 0 M + c - p 0 M × ln ⁡ T T 0

A divisão de c - p 0 por M é o calor específico c p 0 em k J / k g K encontrado em tabelas de gases perfeitos. Ele vale 0,8418   k J / k g K conforme mostrado abaixo!

Agora que conseguimos todos esses valores, vamos aprender a usá-los no próximo passo!

Passo 3

Para usar a fórmula, precisamos somar 273,15 à temperatura T em ° C . Substituindo os valores que temos:

s = s - 0 M + c p 0 × ln ⁡ T T 0

s = 213,795 44,01 + 0,8418 × ln ⁡ 220 + 273,15 298,15  

s = 5,2815   k J k g K

Demos uma volta, mas conseguimos achar a entropia absoluta! Paabéns pra gente!

Resposta

s = 5,2815   k J k g K

Exercício Resolvido #6

Elaboração própria

Determine a entropia absoluta em base mássica do gás metano C H 4 que se encontra a 40 0   ° C e a 0,4   M P a , usando apenas a tabela entropia absoluta das substâncias a 25   ° C e 0,1   M P a .

Passo 1

Oi, galera! Esse exercício pede o valor de entropia absoluta em base mássica s do C H 4 que tem uma temperatura de 40 0   ° C e pressão de 0,4   M P a ! Isso é a mesma coisa que pedir pra gente o valor da entropia por unidade de massa! O problema é só temos tabelas que informam o valor da entropia por unidade de k m o l s - . Logo, precisamos converter s - pela fórmula abaixo!

s = s - M

onde M é a massa molar do C H 4 que vale 16,043   k g / k m o l segundo tabelas de gases.

No entanto, o exercício só permitiu a gente de usar a tabela abaixo que possui a entropia absoluta s - 0 das substâncias a 25   ° C e a 0,1   M P a . Logo, vamos precisar primeiro converter s - 0 pra entropia s - T 0 do C H 4 a 400   ° C e a 0,1   M P a pela fórmula abaixo!

s - T 0 = s - 0 + c - p 0 × ln ⁡ T T 0

onde T é a temperatura em kelvin do C H 4 e T 0 é a temperatura de 298,15   K . c - p 0 é o calor específico a pressão constante em k J / k m o l K .

Depois, vamos precisar converter s - T 0 pra entropia s - do C H 4 a 400   ° C e a 0,4   M P a pela fórmula abaixo!

s - = s - T 0 - R - × ln ⁡ P P 0

R - é a constante universal dos gases. Seu valor de 8,314   k J / k m o l K é igual para todos os gases. P é a pressão de 0,4   M P a na qual o C H 4 está. P 0 é a pressão de tabela em que pegamos o valor da entropia absoluta. No caso, a pressão das tabelas que temos valem 0,1   M P a .

No próximo passo, veremos como pegar o valor s - 0 da tabela!

Passo 2

O valor de s - 0 se encontra abaixo.

s - 0 = 186,251   k J k m o l K

Com esse valor, somos capazes de encontrar o valor da entropia do s - T 0 C H 4 na temperatura de 400   ° C e na pressão de 0,1   M P a pela equação abaixo. No entanto, ainda não conhecemos o valor de c - p 0 do C H 4 . Pra encontrar c - p 0 , precisamos multiplicar o calor específico por unidade de massa c P 0 do C H 4 pela massa molar M do C H 4 ! O c P 0 do C H 4 vale 2,2537   k J / k g K .

c - p 0 = c P 0 × M

c - p 0 = 2,2537 × 16,043

c - p 0 = 36 , 156   k J k m o l K

Agora que conseguimos todos esses valores, vamos aprender a usá-los no próximo passo!

Passo 3

Primeiro, vamos encontrar s - T 0 , substituindo os valores de c - p 0 e s - 0 . Mas cuidado! Antes, de usar a fórmula, precisamos somar 273,15 à temperatura T em ° C .

s - T 0 = s - 0 + c - p 0 × ln ⁡ T T 0

s - T 0 = 186,251 + 36 , 156 × ln ⁡ 40 0 + 273,15 298,15  

s - T 0 = 215 , 6954   k J k m o l K

Em segundo lugar, achamos s - .

s - = s - T 0 - R - × ln ⁡ P P 0

s - = 215 , 6954 + 8,314 × ln ⁡ 0,4 0,1

s - = 227 , 2211   k J k m o l K

Por fim, encontramos s .

s = s - M

s = 227 , 2211 16,043

s = 14 , 16   k J k g K

Que shooooow! Gostei de ver! Esse exercício foi mais longo, mas resolvemos com muita calma!

Resposta

s = 14 , 16   k J k g K

Exercício Resolvido #7

Elaboração própria

Podemos modelar o ar como uma mistura de gases que possui a seguinte análise molar: 21 % de O 2 e 79 % de N 2 . Supondo que o ar se encontra a uma pressão total de 100   k P a e a 40   ° C de temperatura, determine a entropia absoluta do ar.

Passo 1

Oi, meus chuchus! Esse exercício quer que a gente calcule a entropia s - de uma mistura de gases! A entropia da mistura de gases é a soma das entropias de cada gás. No caso, a entropia da mistura s - é igual à entropia do O 2 s - O 2 mais a entropia do N 2 s - N 2 . y O 2 e y N 2 da fórmula abaixo são as frações molares de O 2 e N 2 .

s - = y O 2 s - O 2 + y N 2 s - N 2

No entanto, o O 2 está submetido à pressão parcial P O 2 e o N 2 está submetido à pressão parcial P N 2 . A pressão parcial de O 2 é igual à pressão total P exercida sobre a mistura multiplicada pela fração molar de O 2 y O 2 . A pressão parcial de N 2 é igual à pressão total P   = 100   k P a exercida sobre a mistura multiplicada pela fração molar de N 2 y N 2 .

P O 2 = y O 2 P

P N 2 = y N 2 P

Isso quer dizer que temos um problema! A tabela que temos só serve para gases a 100   k P a de pressão e o exercício quer o valor de entropia pra pressão parciais diferentes de 100   k P a ! Para resolver esse problemão, convertemos a entropia s - T 0 que encontramos nas tabelas que temos na entropia s - que está na pressão parcial que queremos, usando as fórmulas abaixo!

s - O 2 = s - O 2 T 0   - R - × ln ⁡ P O 2 P 0

s - N 2 = s - N 2 T 0   - R - × ln ⁡ P N 2 P 0

R - é a constante universal dos gases. Seu valor de 8,314   k J / k m o l K é igual para todos os gases. P 0 é a pressão de tabela em que pegamos o valor da entropia absoluta. No caso, a pressão das tabelas que temos valem 0,1   M P a = 100   k P a .

No próximo passo vamos iniciar as contas!

Passo 2

Primeiro, vamos calcular as pressões parciais P N 2 e P O 2 através da pressão total P e das frações molares y N 2 e y O 2 .

P O 2 = y O 2 P

P O 2 = 21 100 × 100

P O 2 = 21   k P a

P N 2 = y N 2 P

P N 2 = 79 100 × 100

P N 2 = 79   k P a

É pra essas pressões parciais que temos que calcular as entropias.

Achamos as entropias s - O 2 T 0 do O 2 e s - N 2 T 0 do N 2 nas tabelas de entropia absoluta do O 2 e do N 2 para a temperatura T de 40   ° C . No entanto, pra usar as tabelas, temos que converter T pra kelvin, somando 273,15   K !

T = 40 + 273,15

T = 313,15   K

Uhuuuul! Já temos os valores que precisamos pra achar as entropias nas tabelas!

No próximo passo faremos isso!

Passo 3

s - O 2 T 0 se encontra na tabela de O 2 abaixo. Como podemos ver, não existe um valer de entropia absoluta para a temperatura exata de 313,15   K . Logo, achamos a entropia absoluta s - O 2 T 0 , interpolando a tabela!

s - O 2 T 0 = 205,329 + 213,873 - 205,329 400 - 300 × 313,15 - 300

s - O 2 T 0 = 206,453   k J k m o l K

Pelo mesmo motivo, precisamos achar a entropia s - N 2 T 0 , interpolando a tabela de entropia absoluta de N 2 .

s - N 2 T 0 = 191,789 + 200,181 - 191,789 400 - 300 × 313,15 - 300

s - N 2 T 0 = 192,893   k J k m o l K

Beleza, essas são as entropias para a pressão total de 100   k P a . Na próxima etapa já vamos conseguir terminar o exercício, determinando as entropias s - O 2 e s - N 2 para as pressões parciais!

Passo 4

Agora, precisamos achar as entropias s - O 2 e s - N 2 pras pressões parciais pelas equações abaixo!

s - O 2 = s - O 2 T 0   - R - × ln ⁡ P O 2 P 0

s - O 2 = 206,453   - 8,314 × ln ⁡ 21 100

s - O 2 = 219,4282   k J k m o l K

s - N 2 = s - N 2 T 0   - R - × ln ⁡ P N 2 P 0

s - N 2 = 192,893   - 8,314 × ln ⁡ 79 100

s - N 2 = 194,8528   k J k m o l K

Somando esses dois valores, achamos s - !

s - = y O 2 s - O 2 + y N 2 s - N 2

s - = 21 100 × 219,4282 + 79 100 × 194,8528

s - = 200 , 013   k J k m o l K

Boaaaaaa! Pode respirar aliviado! Esse é um exercício difícil de entropia absoluta e você conseguiu fazer! Isso quer dizer que você está pronto pra sua prova!

Resposta

s - = 200 , 013   k J k m o l K

Exercício Resolvido #8

Elaboração própria

Uma mistura de gases possui a seguinte análise em massa: 20 % de O 2 , 75 % de N 2 e 5 % de C O 2 . Supondo que essa mistura se encontre a uma pressão total de 3 00   k P a e a 6 0   ° C de temperatura, determine a entropia absoluta da mistura.

Passo 1

Oi, meus chuchus! Esse exercício quer que a gente calcule a entropia s - de uma mistura de gases! A entropia da mistura de gases é a soma das entropias de cada gás. No caso, a entropia da mistura s - é igual à entropia do O 2 s - O 2 mais a entropia do N 2 s - N 2 mais a entropia do C O 2 s - C O 2 . y O 2 , y N 2 e y C O 2 da fórmula abaixo são as frações molares de O 2 , N 2 e C O 2 .

s - = y O 2 s - O 2 + y N 2 s - N 2 + y C O 2 s - C O 2

No entanto, o O 2 está submetido à pressão parcial P O 2 , o N 2 está submetido à pressão parcial P N 2 e o C O 2 está a uma pressão parcial de P C O 2 . A pressão parcial de O 2 é igual à pressão total P multiplicada pela fração molar de O 2 y O 2 . A pressão parcial de N 2 é igual à pressão total P   = 100   k P a multiplicada pela fração molar de N 2 y N 2 . P C O 2 é P vezes y C O 2 .

P O 2 = y O 2 P

P N 2 = y N 2 P

P C O 2 = y C O 2 P

Isso quer dizer que temos um problema! A tabela que temos só serve para gases a 100   k P a de pressão e o exercício quer o valor de entropia pra pressão parciais diferentes de 100   k P a ! Para resolver esse problemão, convertemos a entropia s - T 0 que encontramos nas tabelas que temos na entropia s - que está na pressão parcial que queremos, usando as fórmulas abaixo!

s - O 2 = s - O 2 T 0   - R - × ln ⁡ P O 2 P 0

s - N 2 = s - N 2 T 0   - R - × ln ⁡ P N 2 P 0

s - C O 2 = s - C O 2 T 0   - R - × ln ⁡ P C O 2 P 0

R - é a constante universal dos gases. Seu valor de 8,314   k J / k m o l K é igual para todos os gases. P 0 é a pressão de tabela em que pegamos o valor da entropia absoluta. No caso, a pressão das tabelas que temos valem 0,1   M P a = 100   k P a .

No próximo passo vamos iniciar as contas!

Passo 2

Primeiro, vamos calcular as pressões parciais P N 2 , P O 2 P C O 2 . No entanto, pra achar as pressões, precisamos achar as frações molares y N 2 , y O 2 e y C O 2 a partir das porcentagens dos gases na análise em massa! Fazemos isso, através das fórmulas abaixo.

y O 2 = c O 2 M O 2 c O 2 M O 2 + c N 2 M N 2 + c C O 2 M C O 2

y N 2 = c N 2 M N 2 c O 2 M O 2 + c N 2 M N 2 + c C O 2 M C O 2

y C O 2 = c C O 2 M C O 2 c O 2 M O 2 + c N 2 M N 2 + c C O 2 M C O 2

onde c O 2 , c N 2 e c C O 2 são as porcentagens de O 2 , N 2 e C O 2 na análise e M O 2 , M N 2 e M C O 2 são as massas molares de O 2 , N 2 e C O 2 . M O 2 vale 31,999   k g / k m o l , M N 2 vale 28,013 kg/kmol

e M C O 2 vale 44,010   k g / k m o l . Substituindo esses valores, achamos:

y O 2 = 0,2 31,999 0,2 31,999 + 0,75 28,013 + 0,05 44,010 = 0,183

y N 2 = 0,75 28,013 0,2 31,999 + 0,75 28,013 + 0,05 44,010 = 0,784

y C O 2 = 0,05 44,010 0,2 31,999 + 0,75 28,013 + 0,05 44,010 = 0 , 033

Agora podemos encontrar as pressões parciais!

P O 2 = y O 2 P

P O 2 = 0,183 × 3 00

P O 2 = 54,9   k P a

Eba! Encontramos a primeira!

P N 2 = y N 2 P

P N 2 = 0,784 × 3 00

P N 2 = 235,2   k P a

Aeee! A segunda já foi!

P C O 2 = y C O 2 P

P C O 2 = 0 , 033 × 3 00

P C O 2 = 9,9   k P a

Uhull! Achamos a terceira! É pra essas pressões parciais que temos que calcular as entropias.

Achamos as entropias s - O 2 T 0 do O 2 , s - N 2 T 0 do N 2 e s - C O 2 T 0 do C O 2 nas tabelas de entropia absoluta do O 2 , do N 2 e do C O 2 para a temperatura T de 6 0   ° C . No entanto, pra usar as tabelas, temos que converter T pra kelvin, somando 273,15   K !

T = 6 0 + 273,15

T = 33 3,15   K

Já temos os valores que precisamos pra achar as entropias nas tabelas!

No próximo passo faremos isso!

Passo 3

s - O 2 T 0 se encontra na tabela de O 2 abaixo. Como podemos ver, não existe um valer de entropia absoluta para a temperatura exata de 33 3,15   K . Logo, achamos a entropia absoluta s - O 2 T 0 , interpolando a tabela!

s - O 2 T 0 = 205,329 + 213,873 - 205,329 400 - 300 × 33 3,15 - 300

s - O 2 T 0 = 208 , 161   k J k m o l K

Pelo mesmo motivo, precisamos achar a entropia s - N 2 T 0 , interpolando a tabela de entropia absoluta de N 2 .

s - N 2 T 0 = 191,789 + 200,181 - 191,789 400 - 300 × 33 3,15 - 300

s - N 2 T 0 = 194,571   k J k m o l K

Por fim, interpolamos a tabela de entropia absoluta do C O 2 .

s - C O 2 T 0 = 214,024 + 2 25,314 - 214,024 400 - 300 × 333,15 - 300

s - C O 2 T 0 = 217,767   k J k m o l K

Beleza, essas são as entropias para a pressão total de 100   k P a . Na próxima etapa já vamos conseguir terminar o exercício, determinando as entropias s - O 2 , s - N 2 e s - C O 2 para as pressões parciais!

Passo 4

Agora, precisamos achar as entropias s - O 2 , s - N 2 e s - C O 2 pras pressões parciais pelas equações abaixo!

s - O 2 = s - O 2 T 0   - R - × ln ⁡ P O 2 P 0

s - O 2 = 208 , 161   - 8,314 × ln ⁡ 54,9 100

s - O 2 = 213 , 1465   k J k m o l K

Eba, a entropia absoluta de O 2 foi encontrada!

s - N 2 = s - N 2 T 0   - R - × ln ⁡ P N 2 P 0

s - N 2 = 194,571   - 8,314 × ln ⁡ 235,2 100

s - N 2 = 187 , 4603   k J k m o l K

s - C O 2 = s - C O 2 T 0   - R - × ln ⁡ P C O 2 P 0

s - C O 2 = 217,767   - 8,314 × ln ⁡ 9,9 100

s - C O 2 = 236 , 9943   k J k m o l K

Somando esses dois valores, achamos s - !

s - = y O 2 s - O 2 + y N 2 s - N 2 + y C O 2 s - C O 2

s - = 0,183 × 213 , 1465 + 0,784 × 187 , 4603 + 0 , 033 × 236 , 9943

s - = 193 , 795   k J k m o l K

Boaaaaaa! Pode respirar aliviado! Esse é um exercício difícil de entropia absoluta e você conseguiu fazer! Isso quer dizer que você está pronto pra sua prova!

Resposta

s - = 193 , 79   k J k m o l K

Exercícios de Livros Relacionados

A formulação de Planck da terceira lei afirma que uma superfície isentrópica cobre o plano T = 0 K . Deduza a equação ( 7 - 60 ) , mostrando que se esta superfície tivesse um ramo para temperatura mai
Mostre que a formulação da Planck da terceira lei pode ser deduzida da formulação de inacessibilidade.
Um polímero mantido a pressão constante contrai-se quando a temperatura é aumentada. Esboce uma curva do comprimento do polímero em função da temperatura nas proximidades de 0K e ofereça razões para t