Compressores e Bombas
Produzido por Philip Canabarro BlockerTeoria
Qual é a função da bomba?
Imagine que você mora em uma casa que usa água de um poço artesiano. Como você pode fazer a água se mover até o seu chuveiro, se ela está parada no fundo do poço? Não vale dizer que vai pegar a água do poço com um balde! ^^
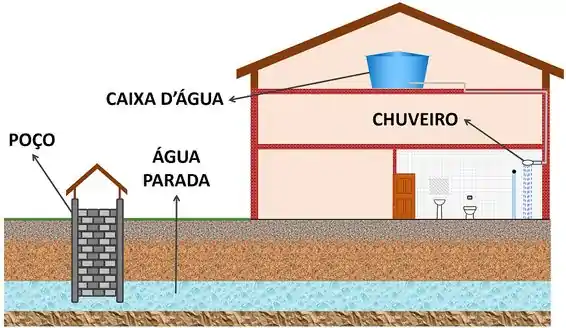
Se a gente puder aumentar a pressão da água que está lá embaixo, ela vai ser conseguir vencer a força do seu próprio peso. Desse jeito, a pressão debaixo vai conseguir empurrar a coluna de líquido que está em cima, até ela alcançar o chuveiro!
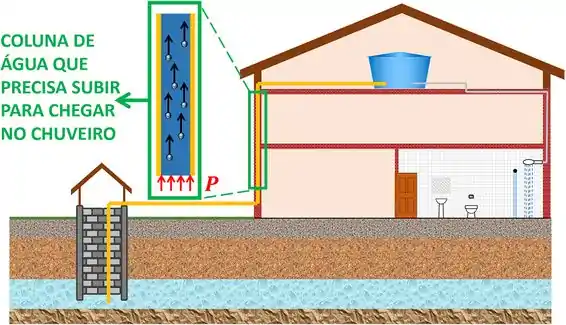
Ótimo! Já descobrimos uma solução! Mas qual equipamento é capaz de aumentar a pressão de um líquido?

A bomba é o equipamento usado para aumentar a pressão de um líquido! O líquido entra nela com uma pressão menor e sai dela com pressão maior e com mais energia por conta desse aumento de pressão! Mas de onde vem essa energia que o líquido ganha? Veremos isso agora!
Como a bomba aumenta a pressão e a energia do líquido?
A energia do líquido aumenta conforme ele passa pela bomba, porque ele recebe energia por trabalho! Um motor faz um eixo girar e esse eixo faz as peças internas da bomba se moverem. Conforme essas partes internas da bomba se movimentam, elas empurram o líquido com uma força. Isso aumenta a pressão e a energia do líquido!
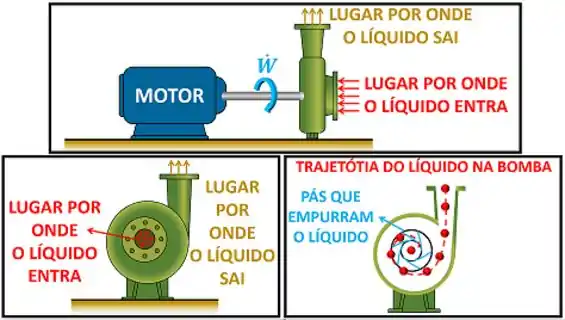
Apesar do movimento dessas peças gerar calor por atrito, é importante saber que essa quantidade de calor é muito pequena. Além disso, a energia cinética e a energia potencial do líquido quase não mudam durante o aumento da pressão. Ou seja, a energia do líquido varia exclusivamente por causa do trabalho realizado sobre ele!
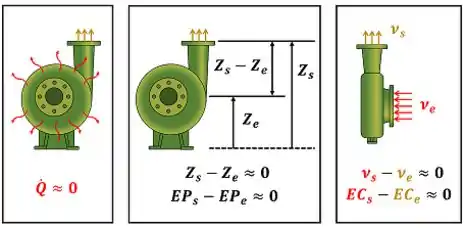
Conhecer esses detalhes do processo é fundamental! Por causa dessas simplificações, a primeira lei para uma bomba funcionando em regime permanente fica bem mais simples!
Primeira lei para uma bomba funcionando em regime permanente
A forma da primeira lei para processos em regime permanente é muito grande!
Como será que ela fica depois da gente desprezar a variação das energias cinética e potencial e depois de considerar que a troca de calor é muito pequena? Podemos descobrir isso, reorganizando a equação da primeira lei.
Lembrando que:
A fórmula vira:
Conseguimos visualizar melhor esses termos através da figura abaixo que mostra uma bomba.
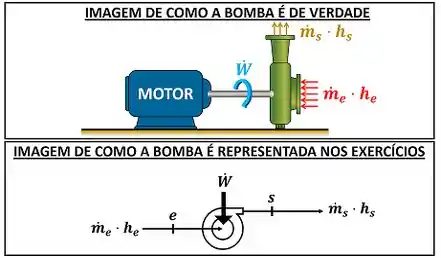
Essa é a equação de conservação de energia para uma bomba. Mas qual seria a forma da equação de conservação de massa para uma bomba funcionando em regime permanente? Nesse caso, toda massa que entra na bomba, sai dela. Ou seja, a conservação de massa da bomba é:
Depois de tanta teoria, vamos fazer uma questão de bomba funcionando em regime permanente para exercitar esse conhecimento novo!
Exercício de uma bomba funcionando em regime permanente
Uma bomba hidráulica está instalada no fundo de um poço e é alimentada com água a e . A vazão mássica de água na bomba é e a pressão da água na saída da bomba vale . Considerando que o processo é adiabático e que a temperatura da água é constante e igual a , determine a potência necessária para ligar a bomba.
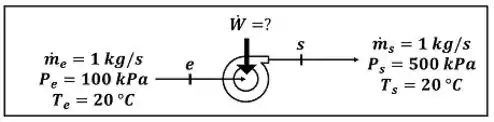
O primeiro passo para resolver esse exercício é entender o que é a potência de acionamento da bomba. Ela é a taxa de trabalho por tempo que a bomba tem que receber de um eixo para movimentar o líquido.

O segundo passo é reescrever a primeira lei da bomba para deixar claro como se calcula essa potência.
Pronto! Agora sabemos que para calcular esse valor, precisamos conhecer quatro variáveis: . Uma delas foi dada diretamente pelo enunciado!
Com esse valor, a vazão mássica de saída da água já pode ser calculada pela fórmula de conservação de massa.
As entalpias de entrada e saída são dadas indiretamente pelo enunciado! Nós encontramos esses dois valores, usando as tabelas de propriedade de água. Para pegar o valor certo, precisamos saber a pressão e a temperatura de entrada da água. Eles são dados pelo problema:
Podemos fazer o mesmo para achar .
Agora, somos capazes de calcular a potência , porque temos todos esses valores em mãos.
Achamos a potência, mas por que ela é negativa?
Isso acontece, porque a vizinhança da bomba está realizando trabalho sobre ela. Isso quer dizer que ela está recebendo energia por trabalho. Sempre quando um sistema fechado ou um volume de controle recebem energia por trabalho, o valor da potência é negativo!
Caso contrário, se o equipamento realizar trabalho sobre sua vizinhança, a potência é positiva!
Qual é a função do compressor?
Vimos até aqui que a bomba é o equipamento usado para aumentar a pressão de um líquido. Mas e se quisermos aumentar a pressão de vapores e gases? Qual equipamento devemos usar?
Devemos usar um compressor!
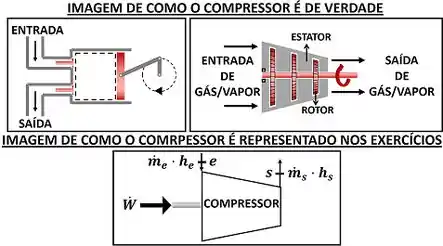
Tanto o compressor quanto a bomba são equipamentos muito parecidos. A única diferença entre eles é que a bomba aumenta a pressão de um líquido e o compressor aumenta a pressão de vapor e gás. Se esses dois equipamentos têm uma única diferença entre si, será que a primeira lei para o compressor é parecida com a primeira lei para a bomba?

Sim! Elas são iguaizinhas! A primeira lei para um compressor funcionando em regime permanente se encontra abaixo!
No entanto, a primeira lei não é a única equação do compressor que é uma cópia de uma equação da bomba! A equação de conservação de massa do compressor também é igualzinha à equação de conservação de massa da bomba!
As semelhanças entre esses dois equipamentos não param por aí! Vimos pelo exercício da bomba, como calculamos a potência que ela precisa consumir para ligar. O cálculo da potência do compressor é feito exatamente da mesma forma! A única diferença é que é um vapor que passa pelo compressor.
![]()
Depois de todas essas informações, está na hora de testarmos o que abamos de ler para fixar bem o conhecimento! Então bora fazer os exercícios!
Primeira lei para uma bomba funcionando em regime permanente
Exercício de uma bomba funcionando em regime permanente
Qual é a função do compressor?
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Uma bomba consome de energia para bombear de água. Determine a variação da entalpia específica da água, considerando que ela escoa em regime permanente através da bomba.
Passo 1
O exercício pede para a gente calcular a variação de entalpia específica da água que passa pela bomba. A figura baixo mostra todos os dados fornecidos pelo enunciado para calcular esse valor.
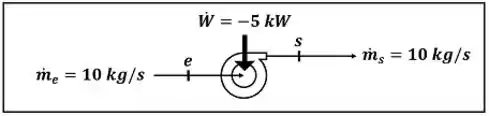
e são as vazões mássicas da água entrando e saindo da bomba respectivamente. é a potência que a bomba consome para funcionar. Atenção, apesar do enunciado dar um valor positivo para essa potência, ela é negativa! Ela é negativa, porque a bomba está sofrendo trabalho. Por uma convenção de sinais, quando um equipamento sofre trabalho, o valor do trabalho e da potência são negativos.
Agora que sabemos o que os dados significam, vamos aprender a calcular .
Passo 2
é calculado a partir da primeira lei usada em uma bomba em regime permanente.
Como e , nós podemos colocar qualquer uma dessas vazões em evidência.
Vamos iniciar as contas no próximo passo!
Passo 3
Resposta
Exercício Resolvido #2
Elaboração própria
Um compressor consome de energia para comprimir de ar. Determine a variação de termperatura do ar, considerando que ele escoa em regime permanente através do compressor.
Passo 1
O exercício pede para a gente calcular a variação de temperatura do ar que passa pelo compressor. A figura baixo mostra todos os dados fornecidos pelo enunciado para calcular esse valor.
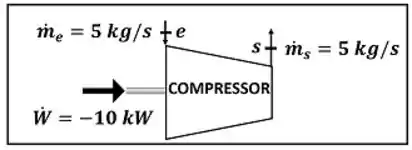
e são as vazões mássicas do ar entrando e saindo do compressor respectivamente. é a potência que o compressor consome para funcionar. Atenção, apesar do enunciado dar um valor positivo para essa potência, ela é negativa! Ela é negativa, porque o compressor está sofrendo trabalho. Por uma convenção de sinais, quando um equipamento sofre trabalho, o valor do trabalho e da potência são negativos.
Agora que sabemos o que os dados significam, vamos aprender a calcular .
Passo 2
é calculado a partir da primeira lei usada em um compressor em regime permanente. Porém, antes de calcular a diferença de temperatura, precisamos calcular a diferença de entalpia .
Como e , nós podemos colocar qualquer uma dessas vazões em evidência.
A diferença de entalpia do ar possui uma fórmula em função do calor específico a pressão constante do ar.
Substituindo essa fórmula na primeira lei, encontramos uma fórmula para .
Vamos iniciar as contas no próximo passo!
Passo 3
A fórmula que precisamos usar já foi criada na etapa acima. O valor de do ar em vale:
Substituindo esse valor na fórmula, encontramos:
Resposta
Exercício Resolvido #3
Elaboração própria
Um compressor consome de energia para comprimir de ar. O ar entra na seção de alimentação do compressor a uma temperatura de . Considerando que a vazão volumétrica de ar na seção de descarga do compressor vale , determine a termperatura e a pressão do ar na seção de descarga do compressor. Suponha que o ar escoa em regime permanente através do compressor.
Passo 1
O exercício pede para a gente calcular a temperatura e a pressão do ar saindo do compressor. A figura baixo mostra todos os dados fornecidos pelo enunciado para calcular esse valor.
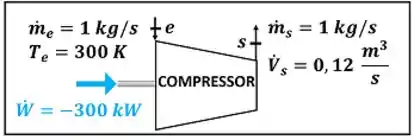
e são as vazões mássicas do ar entrando e saindo do compressor respectivamente. é a vazão volumétrica de ar na saída do compressor. é a temperatura do ar entrando no compressor. é a potência que o compressor consome para funcionar. Atenção, apesar do enunciado dar um valor positivo para essa potência, ela é negativa!

Ela é negativa, porque o compressor está sofrendo trabalho. Por uma convenção de sinais, quando um equipamento sofre trabalho, o valor do trabalho e da potência são negativos.
Agora que sabemos o que os dados significam, vamos aprender a calcular e nos dois próximos passos
Passo 2
é calculado a partir da primeira lei usada em um compressor em regime permanente. Porém, antes de calcular , precisamos calcular a diferença de entalpia .
Como e , nós podemos colocar qualquer uma dessas vazões em evidência.
A diferença de entalpia do ar possui uma fórmula em função do calor específico a pressão constante do ar.
Substituindo essa fórmula na primeira lei, encontramos uma fórmula para .
será encontrado no passo seguinte!
Passo 3
Para encontar , precisamos calcular o volume específico do ar na saída do compressor primeiro. O valor dessa propriedade pode ser achado por meio da relação entre vazão volumétrica e vazão mássica . A vazão mássica é igual à vazão volumétrica multiplicada pela massa específica do ar saindo do compressor .
Com isso, podemos calcular a pressão através da fórmula de gases perfeitos.
onde é a constante de gás do ar que vale .
Substituindo a fórmula de na fórmula de , achamos:
Tendo toda essa informação em mãos, vamos iniciar as contas no próximo passo!
Passo 4
O valor de do ar em que vamos usar na primeira lei vale:
Substituindo esse valor na fórmula, encontramos:
O valor de é calculado abaixo.
Resposta
Exercício Resolvido #4
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 166-6.56
O compressor de uma turbina a gás de grande porte recebe ar do ambiente a uma velocidade baixa e a e . Na saída do compressor, o ar apresenta pressão igual a , temperatura de e velocidade de . Sabendo que a potência de acionamento do compressor é igual a , determine a vazão em massa de ar que escoa na unidade.
Passo 1
Não se assuste! Por mais que o enunciado fale de turbina, a questão é de apenas um equipamento: o compressor. O exercício pede para a gente calcular a vazão mássica que passa pelo compressor. A figura baixo mostra todos os dados fornecidos pelo enunciado para calcular esse valor.
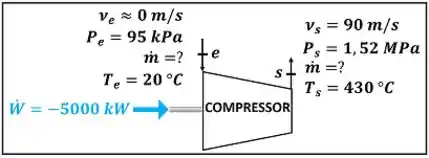
é a vazão mássica do ar entrando e saindo do compressor. e são as temperaturas do ar entrando e saindo do compressor respectivamente. e são as temperaturas do ar entrando e saindo do compressor respectivamente. e são as velocidades do ar entrando e saindo do compressor respectivamente. é a potência que o compressor consome para funcionar.

Atenção, apesar do enunciado dar um valor positivo para essa potência, ela é negativa!
Ela é negativa, porque o compressor está sofrendo trabalho. Por uma convenção de sinais, quando um equipamento sofre trabalho, o valor do trabalho e da potência são negativos.
Agora que sabemos o que os dados significam, vamos aprender a calcular .
Passo 2
é calculado a partir da primeira lei usada em um compressor em regime permanente. Mas cuidado! O enunciado nos informa a velocidade do ar saindo do compressor e diz que a velocidade do ar entrando no compressor é baixa . Isso significa que a forma da primeira lei que precisamos usar tem que levar em conta o termo de energia cinética do ar saindo do compressor . Mas tenha atenção! Precisamos dividir essa energia cinética por mil para passar a unidade desse termo de para .
A diferença de entalpia do ar possui uma fórmula em função do calor específico a pressão constante do ar.
Substituindo essa fórmula na primeira lei, encontramos uma fórmula para .
Tendo toda essa informação em mãos, vamos iniciar as contas no próximo passo!
Passo 3
O valor de do ar em que vamos usar na primeira lei vale:
Substituindo esse valor na fórmula, encontramos:
Resposta
Exercício Resolvido #5
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 166-6.57
Um compressor, refrigerado a água, é alimentado com R-134a a e . O fluido é descarregado do equipamento a e . Sabendo que a taxa de transferência de calor para a água é e que a potência utilizada para acionar o equipamento é , determine a vazão em massa de R-134a no compressor.
Passo 1
O exercício pede para a gente calcular a vazão mássica que passa pelo compressor. A figura baixo mostra todos os dados fornecidos pelo enunciado para calcular esse valor.
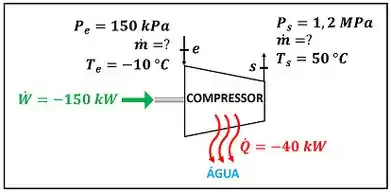
é a vazão mássica de R-134a entrando e saindo do compressor. e são as temperaturas de R-134a entrando e saindo do compressor respectivamente. e são as temperaturas de R-134a entrando e saindo do compressor respectivamente. é a taxa de calor que o compressor perde para a água. é a potência que o compressor consome para funcionar.

Atenção, apesar do enunciado dar um valor positivo para essa potência, ela é negativa!
Ela é negativa, porque o compressor está sofrendo trabalho. Por uma convenção de sinais, quando um equipamento sofre trabalho, o valor do trabalho e da potência são negativos.
O mesmo acontece com a taxa troca de calor ! A convenção de sinais diz que, quando o equipamento perde calor, é negativo!
Agora que sabemos o que os dados significam, vamos aprender a calcular .
Passo 2
é calculado a partir da primeira lei usada em um compressor em regime permanente. Mas cuidado! O enunciado nos informa a taxa de troca de calor entre o R-134a e a água. Isso significa que a forma da primeira lei que precisamos usar tem que levar em conta o termo de taxa de troca de calor !
Para calcular , precisamos encontrar os valores das entalpias específicas do R-134a entrando no compressor e do R-134a saindo do compressor . Nós vamos aprender a fazer isso no próximo passo!
Passo 3
O R-134a entrando no compressor é um vapor superaquecido porque a sua pressão de é menor que a pressão de saturação dessa substância a . Por isso, temos que procurar o valor da entalpia específica na tabela de vapor superaquecido de R-134a. Esse valor está na mesma linha da temperatura de e na mesma coluna que .
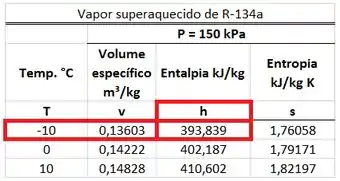
O R-134a saindo do compressor é um vapor superaquecido porque a sua pressão de é menor que a pressão de saturação dessa substância a . Por isso, temos que procurar o valor da entalpia específica na tabela de vapor superaquecido de R-134a. Esse valor está na mesma linha da temperatura de e na mesma coluna que .
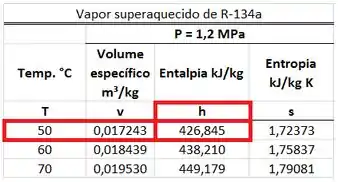
Com esses valores, podemos iniciar as contas!
Passo 4
Resposta
Exercício Resolvido #6
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 167-6.74
A pressão e a temperatura da água que escoa no ramal de distribuição do edifício mostrado na Fig. P6.74 são iguais a e . O ramal está localizado num plano localizado a do chão e a pressão da água na tubulação localizada no andar superior deve ser igual quando a vazão em massa for igual a . Admitindo que as variações de energia cinética dos escoamentos são desprezíveis e que o escoamento é isotérmico, determine a potência necessária para acionar a bomba.
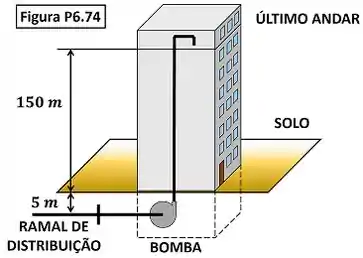
Passo 1
O exercício pede para a gente calcular a potência necessária para acionar a bomba. A diferença desse exercício para um exercício mais simples de bomba é que nesse a gente não analisa só a bomba. Nessa questão a gente vai estudar a bomba mais a tubulação que leva água até o último andar do prédio. A figura baixo mostra todos os dados fornecidos pelo enunciado para calcular esse valor.
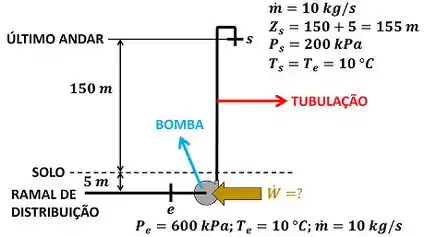
é a vazão mássica de água entrando e saindo da bomba e da tubulação. é a temperatura da água entrando na bomba e é a temperatura da água saindo da tubulação. é a pressão da água entrando na bomba e é a pressão da água saindo da tubulação. é a altura da saída da tubulação em relação ao ramal de distribuição. é a potência que a bomba consome para funcionar.
Agora que sabemos o que os dados significam, vamos aprender a calcular .
Passo 2
é calculado a partir da primeira lei usada em uma bomba em regime permanente. Mas cuidado! O enunciado nos informa a altitude da seção de descarga da tubulação. Isso significa que a forma da primeira lei que precisamos usar tem que levar em conta o termo de energia potencial da água que está saindo da tubulação . Mas CUIDADO! Precisamos dividir essa energia potencial por mil para passar a unidade desse termo de para .
Para calcular , precisamos encontrar os valores das entalpias específicas da água entrando na bomba e da água saindo da tubulação . Nós vamos aprender a fazer isso nos próximos passos!
Passo 3
A água entrando na bomba é um líquido comprimido porque a sua pressão de é maior que a pressão de saturação dessa substância a . Por isso, nós teríamos que procurar o valor da entalpia específica na tabela de líquido comprimido da água. No entanto, não existe tabela de líquido comprimido da água para uma pressão tão baixa.

Por isso, vamos ter que aproximar a entalpia específica da água líquida comprimida a como a soma entre a energia interna da água líquida saturada a e .
onde é o volume específico da água entrando na bomba.
Se considerarmos que a massa específica da água possui um valor típico de , pode ser encontrado.
O valor de está na tabela de saturação, na mesma linha da temperatura de e na mesma coluna que . No entanto, nós não vamos precisar desse valor. O motivo será explicado no próximo passo.
Passo 4
Nós também vamos aproximar como a soma entre a energia interna da água líquida saturada a e .
onde é o volume específico da água saindo da tubulação.
Se considerarmos novamente que a massa específica da água possui um valor típico de , pode ser encontrado.
Ou seja, usamos a mesma aproximação para e . Logo, os dois são iguais e serão cortados da primeira lei.
Com essa nova fórmula, podemos iniciar as contas!
Passo 5
O fato desse valor estar negativo apenas indica que a bomba está sofrendo trabalho. Ou seja, ela está recebendo potência.
Resposta
Exercício Resolvido #7
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 8ª ed. São Paulo: Edgard Blücher, 2018, pp. 189-4.79
Considere uma bomba hidráulica acoplada a um bocal por meio de uma tubulação curta. Os diâmetros das tubulações de alimentação e descarga da bomba são iguais. O diâmetro de descarga do bocal é igual a . A bomba é acionada por um motor de e é alimentada com água a e . O bocal descarrega o fluido na atmosfera a (veja Figura P4.79). Despreze a energia cinética da água no tubo e considere constante a energia interna da água. Determine a vazão mássica de água e a velocidade de descarga.
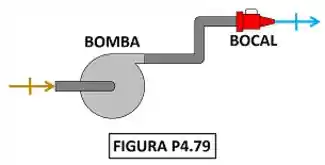
Passo 1
O exercício pede para a gente calcular a vazão mássica de água que passa pela bomba e pelo bocal e a velocidade da água saindo do bocal. A diferença desse exercício para um exercício mais simples de bomba é que nesse a gente não analisa só a bomba. Nessa questão a gente vai estudar a bomba junto com o bocal que faz a velocidade água aumentar na saída! A figura baixo mostra todos os dados fornecidos pelo enunciado para calcular esse valor.
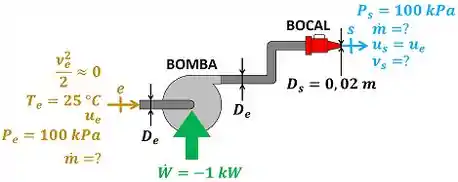
é a vazão mássica de água entrando e saindo da bomba e do bocal. é a temperatura da água entrando na bomba. é a pressão da água entrando na bomba e é a pressão da água saindo do bocal. é a velocidade da água entrando na bomba e é a velocidade da água saindo do bocal. é o diâmetro das duas tubulações que se conectam à bomba. é o diâmetro da saída do bocal. é a energia interna específica da água entrando na bomba. é a energia interna da água saindo do bocal. é a potência que a bomba consome para funcionar.

Atenção, apesar do enunciado dar um valor positivo para essa potência, ela é negativa!
Ela é negativa, porque a bomba está sofrendo trabalho. Por uma convenção de sinais, quando um equipamento sofre trabalho, o valor do trabalho e da potência são negativos.
Agora que sabemos o que os dados significam, vamos aprender a calcular e .
Passo 2
A velocidade é calculada primeiro. O valor dela é encontrado através da primeira lei e da equação vazão mássica. A forma da primeira lei é a primeira lei para bomba incluindo a energia cinética. No entanto, o enunciado nos informa que a energia cinética da água no tubo deve ser desprezada. Isso significa que o termo de energia cinética da água entrando na bomba pelo tubo deve ser considerado nulo.

Mas CUIDADO! O termo de energia cinética da água saindo da bomba não é nulo, porque a velocidade da água saindo do bocal precisa ser calculada! E Atenção Precisamos dividir essa energia cinética por mil para passar a unidade desse termo de para .
O problema dessa fórmula acima é que ainda não conhecemos , nem para calcular . No próximo passo, nós vamos trabalhar em cima dos termos e !
Passo 3
Nós podemos substituir a fórmula das entalpias específicas e em função das energias internas específicas e na primeira lei.
Mas o enunciado diz que é igual a e que é igual a . Logo:
Nós ainda não conhecemos a variação de volume espeífico para conseguir calcular . Por causa disso, nós vamos olhar esse termo mais a fundo no próximo passo!
Passo 4
A água entra na bomba com e a . Logo, ele entra como um liquido comprimido. O líquido compressível quase não varia seu volume específico, quando é bombeado. Por isso:
Por fim, para achar , precisamos achar uma fórmula para a vazão mássica em função da mássica específica da água líquida comprimida a , da velocidade de saída da água e do diâmetro de saída do bocal .
Atenção! Nas questões de termodinâmica, a massa específica da água líquida comprimida a temperatura ambiente geralmente vale:
Substituindo a equação de na primeira lei, nós criamos uma fórmula para .
Sabendo de tudo isso, podemos iniciar as contas.
Passo 5
Além disso, podemos calcular .
Resposta
Exercício Resolvido #8
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 166-6.60
Um dispositivo que opera em regime permanente é alimentado com de amônia a e . A amônia é descarregada do dispositivo a e . As variações de energia cinética e potencial do escoamento de amônia são desprezíveis e o processo realizado no dispositivo pode ser considerado como politrópico. Sabendo que o trabalho específico necessário para acionar um dispositivo é dado por , determine: o expoente politrópico e o trabalho específico e a transferência de calor específica deste processo.
Passo 1
O exercício pede para a gente calcular primeiro o expoente politrópico e depois o trabalho específico e o calor específico . Esse dispositivo recebe trabalho assim como uma bomba e um compressor. Por isso, resolveremos essa questão de forma parecida com as soluções de questões desse equipamento. A figura baixo mostra todos os dados fornecidos pelo enunciado para calcular esses valores.
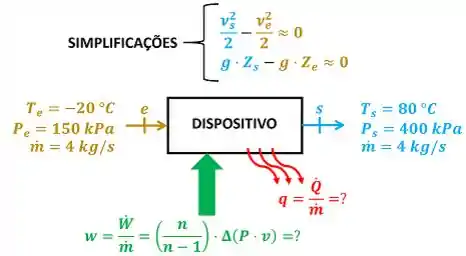
é a vazão mássica de amônia entrando e saindo do dispositivo e do dispositivo. é a temperatura da amônia entrando no dispositivo. é a pressão da amônia entrando no dispositivo e é a pressão da amônia saindo do dispositivo. é a velocidade da amônia entrando no dispositivo e é a velocidade da amônia saindo do dispositivo. é a altitude em relação ao solo da amônia entrando no dispositivo. é a altitude em relação ao solo da amônia saindo do dispositivo. é a potência que o dispositivo consome para funcionar. é a taxa de troca de calor entre o dispositivo e o ambiente. é o trabalho específico que o enunciado pede. é a troca de calor específica que o enunciado pede.

Agora que sabemos o que os dados significam, vamos aprender a calcular .
Passo 2
O expoente politrópico é calculado através da fórmula de processos politrópicos mostrada abaixo.
Essa equação nos diz que o termo se mantém constante durante todo o processo que ocorre dentro do dispositivo. Ou seja, da amônia entrando no dispositivo é igual ao da amônia saindo do dispositivo.
onde e são os volumes específicos da amônia entrando no dispositivo e saindo do dispositivo respectivamente!
Reorganizando essa equação, podemos encontrar uma fórmula para .
A fórmula acima mostra que para calcular , temos que encontrar os valores de e . Faremos isso no próximo passo!
Passo 3
A amônia entrando no dispositivo é um vapor superaquecido porque a sua pressão de é menor que a pressão de saturação dessa substância a . Por isso, temos que procurar o valor do volume específico na tabela de vapor superaquecido da amônia. Esse valor está na mesma linha da temperatura de e na mesma coluna que .
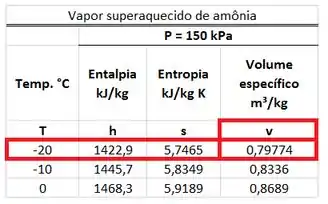
A amônia saindo do dispositivo é um vapor superaquecido porque a sua pressão de é menor que a pressão de saturação dessa substância a . Por isso, temos que procurar o valor do volume específico na tabela de vapor superaquecido da amônia. Esse valor está na mesma linha da temperatura de e na mesma coluna que .
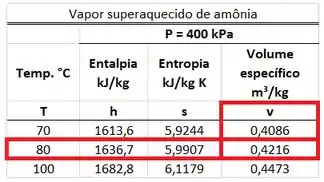
Agor que sabemos quanto valem e , podemos inciar as contas para achar .
Passo 4
Passo 5
Para encontrar o trabalho específico temos que usar a fórmula que o enunciado nos mostrou.
No entanto, é igual a:
Cuidado! Essa fórmula não calcula o trabalho específico com o sinal. O sinal nós teremos que colocar depois! Ele é negativo, porque o dispositivo sofre trabalho!
Com o valor de em mãos, podemos aprender a calcular a troca de calor específica no próximo passo.
Passo 6
A incógnita pode ser calculada através da primeira lei da termodinâmica aplicada ao dispositivo. Lembre-se que o enunciado avisa que as variações de energia cinética e potencial do escoamento de amônia são desprezíveis! Logo os termos de energia cinética e energia potencial não estão presentes na fórmula. No entanto, ao contrário da primeira lei para compressores, a taxa de troca de calor está presente para ser calculada.
A fórmula acima mostra que precisamos encontrar os valores de e para calcular .
Passo 7
Como a amônia que entra no dispositivo é um vapor superaquecido, temos que procurar o valor da entalpia específica na tabela de vapor superaquecido da amônia. Esse valor está na mesma linha da temperatura de e na mesma coluna que .
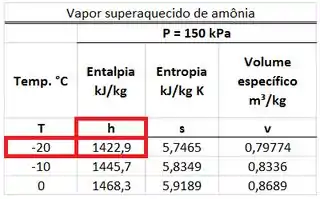
Como a amônia que sai do dispositivo é um vapor superaquecido, temos que procurar o valor da entalpia específica na tabela de vapor superaquecido da amônia. Esse valor está na mesma linha da temperatura de e na mesma coluna que .
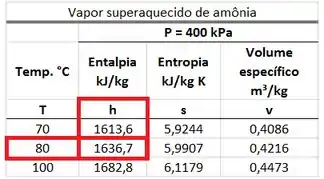
Tendo todos esses valores, podemos começar nossas contas!
Passo 8
Esse resultado não possui o sinal de ainda. Como é negativo, precisamos colocar um sina lde menos no valor acima.
Substituindo esse valor na fórmula de , encontramos: