Turbinas e Restrições
Produzido por Philip Canabarro BlockerTeoria
Qual é a função das turbinas?
Na teoria passada a gente falou sobre bombas e compressores. A bomba aumenta a pressão de um líquido, mas para isso precisa consumir trabalho. O compressor aumenta a pressão de um vapor ou gás, mas para isso ele também precisa consumir trabalho. Ou seja, para aumentar a pressão desses fluidos, esses equipamentos precisam gastar energia na forma de trabalho.
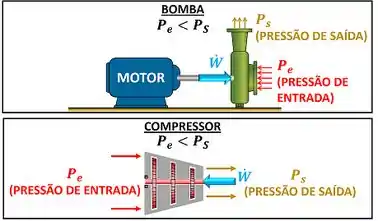
Se existem equipamentos que aumentam a pressão de um fluido (vapor, gás ou líquido) gastando trabalho, será que existe um equipamento que diminui a pressão de um fluido, mas gera trabalho? Ele seria mais ou menos uma bomba ou um compressor que funciona de forma inversa! Isso seria útil, porque ele geraria energia na forma de trabalho de eixo!
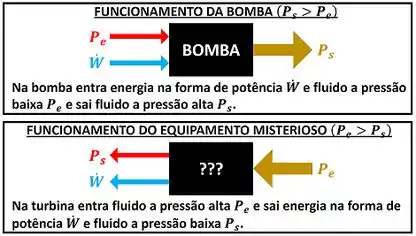
Esse equipamento existe! Ele é chamado de turbina. A sua função é gerar trabalho de eixo através da passagem de vapor, gás ou líquido pelas suas pás. Os detalhes de como isso acontece vão ser mostrados a seguir.
Como a turbina gera potência?
As pás da turbina são presas a um eixo. Conforme o vapor, o gás ou o líquido passam por elas, as moléculas se chocam com as pás. Isso movimenta as pás e faz o eixo girar! Isso é muito parecido com o que acontece, quando bate vento em um cata-vento! Essa produção de movimento também é chamada de geração de potência!
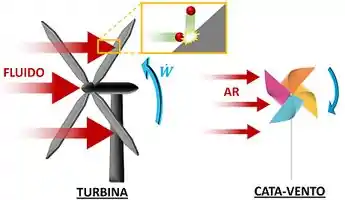
Explicando de outra forma, quando as moléculas de fluido batem na pá, elas perdem pressão. Mas quanto menor a pressão do fluido, menor a agitação das moléculas e menor a sua energia. Isso quer dizer que as moléculas perdem energia e transferem energia pra pá no momento do choque!

Quando o fluido passa pela turbina, falamos que ele sofre um processo de expansão. O processo tem esse nome, porque, quando o fluido perde pressão, o seu volume específico aumenta. Ou seja, o fluido se expande! Mas cuidado para não se confundir! Se o fluido for um líquido, o seu volume específico quase não aumenta! Às vezes essa expansão é desprezível!
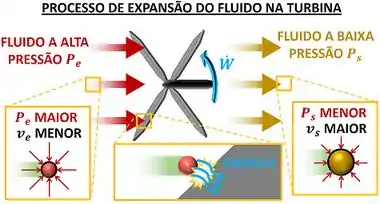
Turbina a gás ou turbina a vapor
Por mais que existam turbinas que funcionem com líquido, focaremos nos dois tipos de turbina que costumam cair em exercícios de termodinâmica: a turbina a vapor e a turbina a gás.
A maior diferença entre essas duas classes de turbina está no tipo de fluido que passa por elas. Na turbina a gás passa gás e na turbina a vapor passa vapor.
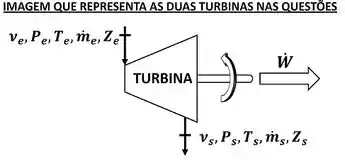
Mas essa não é a única diferença entre elas! Existe outra! Saber dela vai te ajudar a resolver exercícios de termodinâmica! No entanto, para entender melhor a importância dessa diferença, precisamos conhecer antes a equação da primeira lei para essas máquinas.
![]()
Por causa disso, precisamos primeiro resolver uma dúvida: se as duas classes de turbina são diferentes entre si, será que as suas equações de primeira lei e balanço de massa também são muito diferentes?
Na verdade esse não é o caso! As equações delas são iguaizinhas e veremos o motivo a seguir!
Primeira lei e conservação de massa para turbinas funcionando em regime permanente
Os dois tipos de turbina têm fórmulas iguais, porque elas funcionam de uma forma muito parecida. Para os dois casos, as variações de energia potencial e cinética dos fluidos são desprezíveis. Isso ocorre, porque a velocidade do gás e do vapor quase não varia e as alturas de entrada e saída são praticamente iguais !
![]()
Além disso, a troca de calor da turbina para o meio ambiente é muito pequena, porque as turbinas são bem isoladas termicamente. Por isso, nós podemos considerar que o processo na turbina é adiabático !
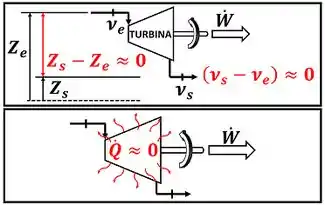
Levando essas aproximações em conta, a primeira lei para turbinas em regime permanente fica mais simples! Para ver isso, temos que reorganizar a equação da primeira lei.
Lembrando que:
A fórmula vira:
Pela regra de sinais da potência, deve sempre ser positivo para a turbina. Isso ocorre, porque a turbina realiza trabalho. Em outras palavras, ela dá energia para sua vizinhança.
Já conhecemos a equação de conservação de energia para uma turbina. Mas qual seria a forma da equação de conservação de massa para uma turbina funcionando em regime permanente? Nesse caso, toda massa que entra nela, sai dela. Ou seja, sua conservação de massa é:
Diferença importante entre turbina a gás e turbina a vapor
Nem sempre os exercícios de termodinâmica nos dão diretamente o valor de pressão do fluido na saída da turbina ! As vezes, só do exercício nos falar o tipo de turbina que estudaremos, ele já está te informando indiretamente o valor de ! Essa informação vai ser muito importante para descobrirmos o valor da entalpia específica na saída do equipamento !
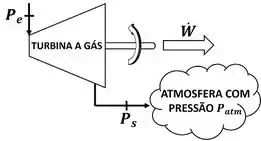
Geralmente, a turbina a gás descarrega o gás na atmosfera. Isso quer dizer que a pressão de saída do gás é igual à pressão atmosférica ! Ou seja, nos exercícios de turbina a gás a pressão geralmente vale:
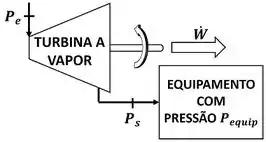
Já a turbina a vapor descarrega o vapor em outro equipamento! Isso quer dizer que a pressão de saída do vapor tem que ser igual à pressão presente nesse equipamento ! Ou seja, nos exercícios de turbina a vapor a pressão geralmente vale:
Qual é a função das restrições?
Imagine que você mora no primeiro andar de um prédio com doze andares. Por causa disso, a pressão da água que sai nas torneiras do seu apartamento é muito alta! Tão alta que você se molha todo quando vai lavar a louça, porque respinga água pra todo lado! Por isso, você quer encontrar uma maneira de reduzir a pressão da água. Qual equipamento usamos pra isso?
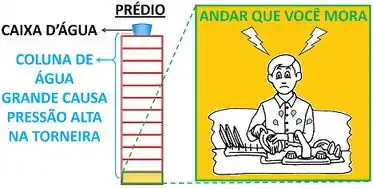
Atenção! Dessa vez nós só queremos um equipamento para diminuir a pressão de um fluido (líquido, vapor e gás). Nós não queremos nem precisamos gerar potência. Por isso, a turbina não é adequada! Ela é um equipamento muito caro e é muito grande.

O equipamento capaz de diminuir a pressão de um fluido é chamado de restrição ou dispositivo de estrangulamento. A restrição coloca um obstáculo na passagem de fluido. Com isso, as moléculas do fluido se chocam com a barreira e perdem pressão! Como existem vários tipos de obstáculo, existem vários tipos restrições.
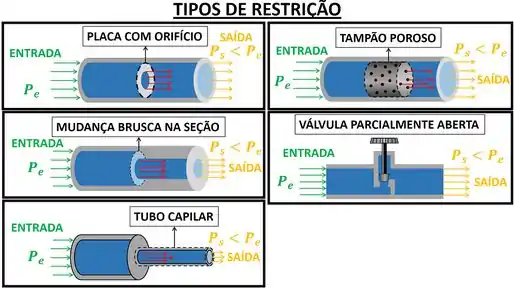
Falamos que quando um fluido passa por uma restrição, ele sofre o processo de estrangulamento! E como seria a forma da primeira lei para esse processo?
Veremos isso agora!
Primeira lei e conservação de massa para restrições em regime permanente
Atenção! A queda de pressão no fluido através da restrição é quase sempre acompanhada por uma grande queda na temperatura! Mas cuidado! Isso não quer dizer que o fluido troca calor com o ambiente! Não faça essa confusão na prova! O estrangulamento é adiabático !
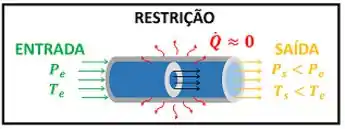
Existe outra confusão muito comum de fazerem! No caso do bocal, a queda de pressão gerava um aumento muito grande na velocidade do fluido! Por isso, a energia cinética variava muito! Esse não é o caso da restrição. A velocidade do fluido aumenta pouco por causa dela. Isso quer dizer que a variação de energia cinética do fluido que passa pela restrição é desprezível!

Além disso, não existe variação de energia potencial nem troca de energia por trabalho ! Com todas essas simplificações, a primeira lei para a restrição fica bem simples!
Para a restrição, toda massa que entra, sai na mesma quantidade. Logo, sua conservação de massa é:
Usando essa equação na primeira lei, podemos cortar as vazões presentes nos dois lados!
Turbina a gás ou turbina a vapor
Primeira lei e conservação de massa para turbinas funcionando em regime permanente
Diferença importante entre turbina a gás e turbina a vapor
Qual é a função das restrições?
Primeira lei e conservação de massa para restrições em regime permanente
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Uma turbina gera através do fluxo de de vapor d’água que passa por ela. Determine a variação da entalpia específica da água, considerando que ela escoa em regime permanente através da turbina.
Passo 1
O exercício pede para a gente calcular a variação de entalpia específica da água que passa pela turbina. A figura baixo mostra todos os dados fornecidos pelo enunciado para calcular esse valor.
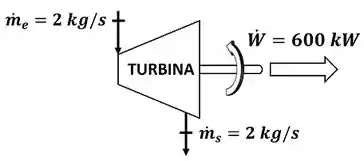
e são as vazões mássicas da água entrando e saindo da turbina respectivamente. é a potência que a turbina gera.
Agora que sabemos o que os dados significam, vamos aprender a calcular .
Passo 2
é calculado a partir da primeira lei para turbinas em regime permanente.
Como e são iguais, nós podemos colocar qualquer uma dessas vazões em evidência.
Vamos iniciar as contas no próximo passo!
Passo 3
Resposta
Exercício Resolvido #2
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 166-6.49
Uma turbina pequena e de alta velocidade é alimentada com ar comprimido e produz uma potência de . O estado na seção de entrada da turbina é e e o estado na seção de saída é e . Admitindo que as velocidades sejam baixas e que a turbina seja adiabática, determine a vazão de ar necessária na turbina.
Passo 1
A questão pede que a gente calcule o valor da vazão mássica de ar que passa pela turbina. A figura abaixo mostra todos os dados informados pelo enunciado que devemos usar pra encontrar esse valor.
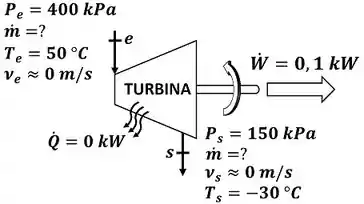
é a temperatura do ar entrando na turbina e é a temperatura do ar saindo da turbina. é a pressão do ar entrando na turbina e é a pressão do ar saindo da turbina. é a velocidade do ar entrando na turbina e é a velocidade do ar saindo da turbina. é a potência gerada pela turbina. é a taxa de calor trocada entre a turbina e o ambiente.

Agora que entendemos todos os dados que nos foram dados, vamos aprender a calcular na próxima etapa.
Passo 2
Calculamos através da equação da primeira lei da turbina em regime permanente. Como o enunciado diz que as velocidades e são muito pequenas, podemos tirar os termos de energia cinética do ar da equação. Além disso, o enunciado diz que o processo de expansão do ar é adiabático. Por isso, também tiramos o termo de taxa de troca de calor da equação.
Na fórmula acima, podemos ver que para calcular o valor de , precisamos encontrar o valor da diferença entre as entalpias específicas do ar e .
Como o ar pode ser considerado um gás perfeito, pode ser calculado através da fórmula abaixo.
onde é o calor específico do ar a pressão constante. Ele vale:
Atenção! As duas temperaturas presentes nessa fórmula tem que estar em kelvin . No entanto, estamos apenas interessados nas diferenças de temperaturas. Além disso, a diferença de temperatura em kelvin é igual à diferença de temperatura em grau Celsius . Por isso, podemos substituir os valores das temperaturas em grau Celsius na fórmula!
Substituindo essa fórmula na equação da primeira lei, encontramos:
Sabendo disso, podemos iniciar as contas!
Passo 3
Resposta
Exercício Resolvido #3
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 165-6.40
Hélio é estrangulado de e até a pressão de . Os diâmetros do tubo de alimentação e descarga são tais que as velocidades de saída e entrada são iguais. Determine a temperatura de saída do hélio e a razão entre os diâmetros dos tubos.
Passo 1
O primeiro passo para resolver essa questão é saber por qual equipamento o hélio está passando para diminuir sua pressão. A resposta para isso é encontrada no enunciado, quando ele diz que o hélio é “estrangulado”. Quando o texto diz que uma substância está sendo estrangulada, ele quer dizer que ela está passando por uma restrição!

O exercício quer saber a temperatura do hélio saindo da restrição e a relação entre os diâmetros do tubo de entrada e saída que estão conectados à restrição. Para encontrar esses valores, temos que entender todos os dados que o enunciado nos informa. A figura abaixo mostra esses dados.
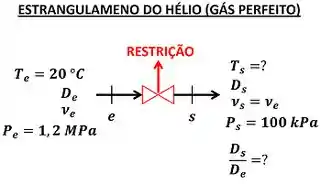
é a temperatura do hélio entrando na restrição e é a temperatura do hélio saindo da restrição. é a pressão do hélio entrando na restrição e é a pressão do hélio saindo da restrição. é a velocidade do hélio entrando na restrição e é a velocidade do hélio saindo da restrição. é o diâmetro do tubo por onde o hélio passa para entrar na restrição e é o diâmetro do tubo por onde o hélio passa quando sai da restrição.

Agora que sabemos disso tudo vamos aprender a calcular a temperatura e a relação nos próximos passos!
Passo 2
A gente encontra através equação da primeira lei para restrições que está abaixo.
Ela diz que a entalpia específica do gás hélio entrando na restrição é igual à entalpia específica do gás hélio saindo sa restrição .
Quando o gás hélio aparece em um exercício de termodinâmica, ele geralmente é um gás perfeito. Para um gás perfeito, a função de cálculo das entalpias só depende da temperatura. Logo, para esse exercício, as entalpias e dependem só das temperaturas.
Para as duas entalpias serem iguais, o valor das temperaturas precisam ser iguais. Logo:
Agora vamos aprender a calcular !
Passo 3
A razão é encontrada através da equação de conservação de massa da restrição em regime permanente. Ela diz que a vazão mássica de entrada é igual à vazão mássica de saída . É importante lembrar também que essas vazões são iguais ao produto entra massa específica do hélio , velocidade do hélio e área de passagem do hélio .
onde e são os volumes específicos do hélio entrando e saindo da restrição respectivamente.
No entanto, o enunciado diz que as duas velocidades e devem ser iguais. Logo, elas podem ser cortadas dos dois lados da equação acima, assim como o e o !
Além disso, como o hélio é um gás perfeito, os volumes específicos e podem ser calculados pela equação de gás perfeito.
Como as duas temperatura são iguais, elas são cortadas dos dois lados da equação!
Substituindo isso na equação de conservação de massa, achamos:
Agora que temos fórmulas para calcular todos os valores que queremos, vamos iniciar as contas!
Passo 4
Antes de usar o valor de na fómula ele precisa estar na mesma unidade de .
Resposta
Exercício Resolvido #4
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 165-6.43
Vapor d’água saturado a é estrangulado, numa válvula parcialmente aberta, até a pressão de . Admitindo que o processo seja adiabático e que as variações de energia cinética e potencial são desprezíveis, determine a temperatura do vapor após o estrangulamento.
Passo 1
O enunciado diz que o vapor d’água saturado é estrangulado numa válvula parcialmente. Essa válvula é uma restrição ao escoamento da água. O exercício quer saber a temperatura da água saindo da restrição. Para encontrar ess valor, temos que entender todos os dados que o enunciado nos informa. A figura abaixo mostra esses dados.
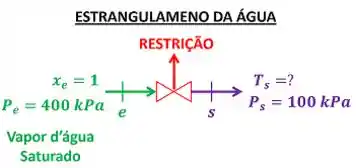
é a pressão da água entrando na restrição e é a pressão da água saindo da restrição. é o título da água entrando na restrição. Como a água que entra na restrição é um vapor saturado, o seu título é igual a .
Agora que sabemos disso tudo vamos aprender a calcular a temperatura nos próximos passos!
Passo 2
A gente encontra através equação da primeira lei para restrições que está abaixo.
Nós só podemos saber primeiro qual é o valor da entalpia específica , porque apenas o estado da água entrando na restrição é que está definido pelo valor de duas propriedades ( e ).
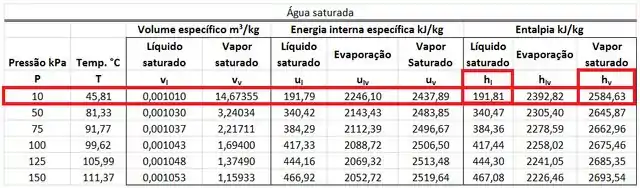
pode ser encontrada em uma tabela de saturação da água. Esse valor está na mesma linha da pressão de e na mesma coluna da entalpia específica do vapor saturado .
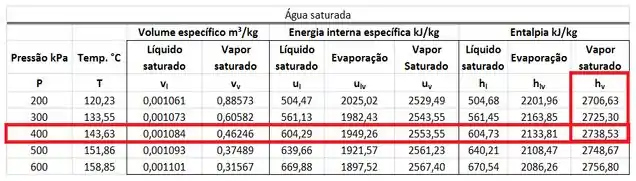
Como é igual a , vale:
Isso significa que nós determinamos já determinamos o estado de saída da água, porque temos o valor de duas propriedades: a sua entalpia e a sua pressão .
No próximo passo vamos descobrir a primeira etapa para encontrar a temperatura a partir dessa nova informação.
Passo 3
Se for maior que a entalpia específica do vapor saturado a , a água está na forma de vapor superaquecido.
Se for menor que a entalpia específica do líquido saturado a , a água está na forma de líquido comprimido.
Se for maior que a entalpia específica do líquido saturado a e menor que a entalpia específica do vapor saturado a , a água está saturada.
Os valores de e são achados na tabela de saturação da água para uma pressão de . está na mesma linha da pressão de e na mesma coluna que a entalpia do líquido saturado . está na mesma linha da pressão de e na mesma coluna que a entalpia do líquido saturado .
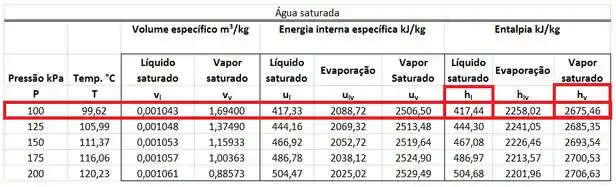
Como é maior que , a água da saída da restrição é um vapor superaquecido e teremos que achar o valor de através de uma tabela de vapor superaquecido. Deixaremos essa parte para o próximo passo.
Passo 4
A tabela de vapor superaquecido a se encontra abaixo. Nessa tabela não existe o valor de temperatura da água, quando sua entalpia específica vale tanto quanto . Só temos a temperatura para uma entalpia menor de e uma temperatura para uma entalpia maior de . A entalpia que temos está no meio dessas duas. Por isso, vamos ter que interpolar o valor de .
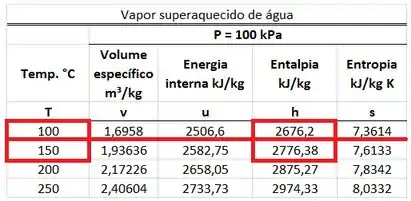
Resposta
Exercício Resolvido #5
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 165-6.48
Uma turbina é alimentada com de vapor a e . O vapor é descarregado da turbina como vapor saturado a . Sabendo que a velocidade na seção de alimentação da turbina é igual a e que a velocidade na seção de descarga é pequena, determine o trabalho específico e a potência gerada pela turbina.
Passo 1
A questão pede que a gente calcule o valor da taxa de trabalho (potência) realizado pela turbina e também pede que a gente calcule a divisão entra a potência e a vazão mássica de vapor que é chamada de trabalho específico. A figura abaixo mostra todos os dados informados pelo enunciado que devemos usar pra encontrar esses valores.
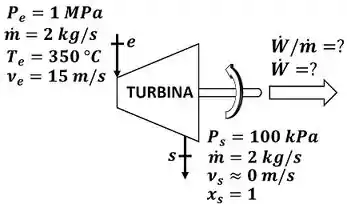
é a temperatura do vapor entrando na turbina e é a temperatura do vapor saindo da turbina. é a pressão do vapor entrando na turbina e é a pressão do vapor saindo da turbina. é a vazão mássica de vapor que passa pela turbina. Ela é igual na entrada e na saída, porque a turbina está funcionando em regime permanente.

é a velocidade do vapor entrando na turbina e é a velocidade do vapor saindo da turbina.
é o título do vapor saindo da turbina. Como o vapor saindo da turbina está saturado, o título vale .
Agora que entendemos todos os dados que nos foram dados, vamos aprender a calcular e na próxima etapa.
Passo 2
Calculamos e através da equação da primeira lei da turbina em regime permanente. Mas tenha ATENÇÃO! O enunciado diz que o valor da velocidade de entrada do vapor vale . Ou seja, precisamos levar em conta a energia cinética do vapor na entrada da turbina. Como o enunciado diz que é pequena, podemos desprezar a energia cinética do vapor na saída da turbina.
Na fórmula acima, vemos que o termo da energia cinética está dividido por . Isso é necessário para passar a unidade desse termo de para .
Além disso, podemos ver que para calcular o valor de , precisamos encontrar os valores de e . No próximo passo veremos como fazer isso.

Despois de calcular , calculamos o trabalho específico , dividindo por pela vazão mássica .
Passo 3
A entalpia específica do vapor entrando na turbina para uma pressão de e uma temperatura de só pode ser encontrada na tabela de vapor superaquecido. Ela está na mesma linha que a temperatura de e na mesma coluna que .
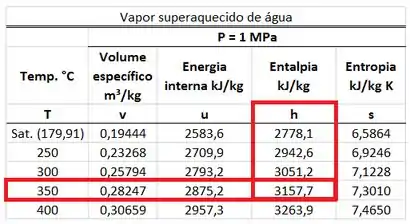
Como o vapor saindo da turbina está saturado, encontramos o valor de na tabela de saturação da água. Ela está na mesma linha que a pressão de e na mesma coluna que a entalpia do vapor saturado .
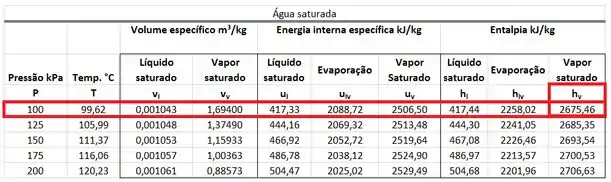
Com esses dois valores já podemos partir para as contas!
Passo 4
Dividindo esse valor pela vazão mássica, encontramos o trabalho específico realizado pela turbina.
Resposta
Exercício Resolvido #6
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 166-6.53
A Fig. P6.53 mostra o esquema de uma pequena turbina a vapor d’água que produz uma potência de operando em carga parcial. Nesta condição, a vazão de vapor é , a pressão e a temperaturana seção são, respectivamente, iguais a e e o vapor é estrangulado até antes de entrar na turbina. Sabendo que a pressão de saída da turbina é , determine o título; ou a temperatura, se o vapor estiver superaquecido; da água na seção de saída da turbina.
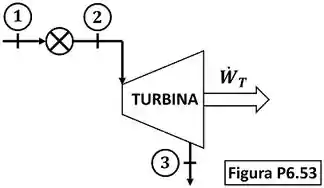
Passo 1
Essa questão envolve dois equipamentos: a restrição que está entre os estados e da água e a turbina que está entre os estados e da água. O enunciado pede que a gente encontre o valor do título ou a temperatura da água que está saindo da turbina no estado . A figura abaixo mostra todos os dados informados pelo enunciado que devemos usar pra encontrar esses valores.
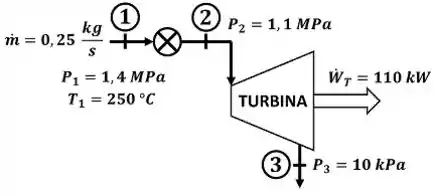
é a temperatura do vapor d’água entrando na restrição e é a temperatura da água saindo da turbina. é a pressão do vapor d’água entrando na restrição, é a pressão da água entrando na turbina e é a pressão da água saindo da turbina. é a vazão mássica de água que passa pela turbina e pela restrição. é a potência gerada pela turbina. é o título da água saindo da turbina.

Agora que entendemos todos os dados que nos foram dados, vamos aprender a calcular e na próxima etapa.
Passo 2
Para encontrar as propriedades do estado e nós precisamos determinar o estado da água saindo da turbina. Nós fazemos isso descobrindo o valor de duas propriedades da água nesse estado . Um já foi dado. É a pressão que vale . O outro valor que podemos descobrir é a entalpia especifica da água saindo da turbina. Ela é encontrada através da equação da primeira lei para turbina que está abaixo.
Na fórmula acima, podemos ver que para calcular o valor de , precisamos encontrar o valor de . é encontrado através da equação da primeira lei para restrições mostrada abaixo.
Ou seja, o valor de é igual ao valor de . No próximo passo vamos aprender a encontrar o valor de .
Passo 3
A entalpia específica do vapor entrando na restrição para uma pressão de e uma temperatura de só pode ser encontrada na tabela de vapor superaquecido. Ela está na mesma linha que a temperatura de e na mesma coluna que .
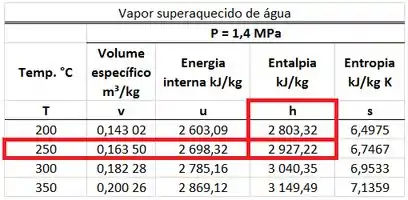
Isso quer dizer que:
Com esse valor encontramos . Mas como podemos encontrar ou através da entalpia especifica ?
Veremos isso no próximo passo!
Passo 4
Atenção! A água que sai de uma turbina a vapor NUNCA será um líquido comprimido, porque isso danificaria o equipamento. Ou seja, a água do estado (que esta saindo da turbina) só pode estar em duas fases: ou saturada ou vapor superaquecido. Se ela for saturada, o exercício pede que a gente calcule e , se ela for um vapor superaquecido, o exercício pede .
Para decidir se a água do estado é saturada ou não, precisamos encontrar o valor de entalpia do vapor saturado a . Se a entalpia for maior que , então a água é um vapor superaquecido. Se a entalpia for menor que , então ela está saturada. Caso ela esteja saturada, calculamos o título através da fórmula abaixo.
onde é a entalpia da água líquida saturada .
A temperatura da água saturada a é encontrada em uma tabela de saturação da água na mesma linha que a pressão de e na mesma coluna que .
e são encontrados na tabela de saturação da água na mesma linha que a pressão de .
Caso a água seja um vapor superaquecido, a temperatura é encontrada em uma tabela de vapor superaquecido para pressão de e entalpia de .
Sabendo disso, podemos iniciar as contas.
Passo 5
A entalpia é calculada abaixo.
Comparando o valor acima com a entalpia do vapor saturado a , percebemos que é menor! Isso significa que a água que sai da turbina no estado está saturada e precisamos encontrar com a fórmula abaixo.
A temperatura é encontrada na tabela de saturação da água abaixo.
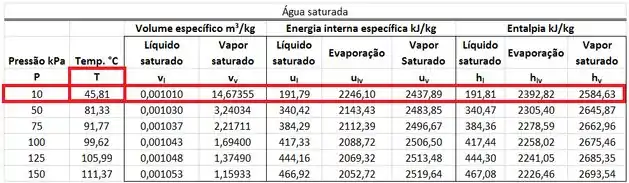
Resposta
Exercício Resolvido #7
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 168-6.78
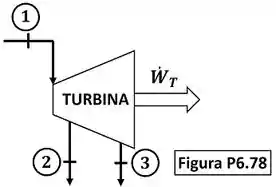
Uma turbina é alimentada com de vapor d’água a e . Num estágio intermediário, onde e , é realizada a extração de (ver Fig. P6.78). Na seção final de descarga, a pressão e o título são respectivamente, iguais a e . Admitindo que a turbina seja adiabática e que as variações de energia cinética e potencial sejam desprezíveis, determine a potência da turbina.
Passo 1
Esse é um exercício de turbina diferente, porque essa turbina, ao contrário das turbinas comuns, têm duas vazões de saída! A questão pede que a gente calcule a potência gerada pela turbina. A figura abaixo mostra todos os dados informados pelo enunciado que devemos usar pra encontrar esse valor.
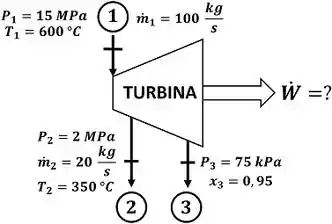
é a temperatura do vapor d’água entrando na turbina, é a temperatura da água saindo da turbina pela saída intermediária. é a pressão do vapor d’água entrando na turbina, é a pressão da água saindo da turbina pela saída intermediária e é a pressão da água saindo da turbina pela saída final. é a vazão mássica de água entrando na turbina e é a vazão mássica de água saindo da turbina pela saída intermediária. é o título da água saindo da turbina pela saída final.

Agora que entendemos todos os dados que nos foram dados, vamos aprender a calcular próxima etapa.
Passo 2
Calculamos através da primeira lei da termodinâmica aplicada a uma turbina que funciona em regume permanente. Mas cuidado. Esse caso é diferente do que estamos acostumados. Ele inclui mais um termo de entalpia específica!
onde , e são as entalpias específicas das correntes de água , e .
Os termos das energias cinética e potencial e da taxa de troca de calor não estão presentes na equação, porque o enunciado disse que eles são desprezíveis.
pode ser calculado através da equação de conservação de massa.
Podemos ver pela primeira lei que precisamos determinar os valores de , e para calcular . Faremos isso na próxima etapa!
Passo 3
A entalpia da corrente de água só pode ser encontrada na tabela de vapor superaquecido para uma pressão de e . Ela está na mesma linha que a temperatura de e na mesma coluna que .
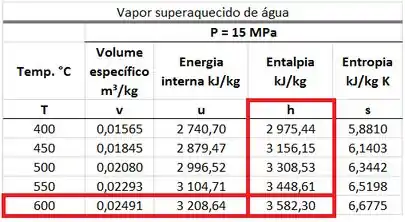
A entalpia da corrente de água só pode ser encontrada na tabela de vapor superaquecido para uma pressão de e . Ela está na mesma linha que a temperatura de e na mesma coluna que .
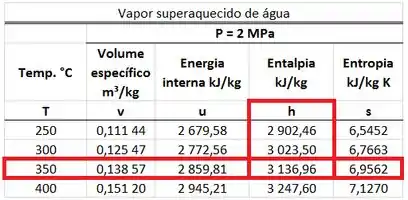
A entalpia da corrente de água só pode ser encontrada na tabela de água saturada, porque ela tem um título. Ela é uma mistura entre a entalpia específica do líquido saturado a e a entalpia específica do vapor saturado a . Para calcular , precisamos da fórmula abaixo.
está na mesma linha que a pressão de na mesma coluna que da tabela. está na mesma linha que a pressão de na mesma coluna que da tabela.
Com todos esses valores em mãos, podemos finalmente iniciar as contas.
Passo 4
Vamos começar os cálculos, determinando quanto vale .
Agora vamos determinar o valor de .
Agora sim podemos calcular .
Resposta
Exercício Resolvido #8
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 171-6.105
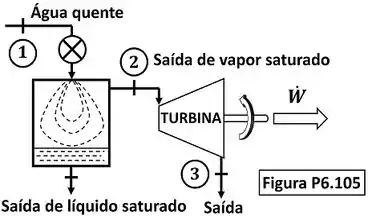
Propõe-se usar um suprimento geotérmico de água quente para acionar uma turbina a vapor d’água utilizando o dispositivo esquematizado na figura P6.105. Água a alta pressão, e , é estrangulada, num evaporador instantâneo adiabático, de modo a obter líquido e vapor a pressão de . O líquido sai pela parte inferior do evaporador, enquanto o vapor é retirado para alimentar a turbina. O vapor sai da turbina a e com título igual a . Sabendo que a turbina produz uma potência de , qual é a vazão necessária de água quente, em , que deve ser fornecida pela fonte geotérmica?
Passo 1
O enunciado pode assustar por conta da quantidade de informação, mas pode relaxar! Essa questão envolve dois equipamentos que conhecemos bem: a restrição que estrangula o vapor e a turbina que gera potência!

A questão quer que a gente calcule a vazão de água quente que entra na restrição. A figura abaixo mostra todos os dados informados pelo enunciado que devemos usar pra encontrar esse valor.
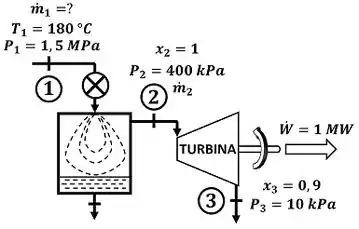
é a temperatura da água entrando na restrição. é a pressão da água entrando na restrição, é a pressão da água entando na turbina e é a pressão da água saindo da turbina. é a vazão mássica de água entrando na restrição e é a vazão mássica de água passando pela turbina. é o título da água entrando na turbina. Ele vale , porque a figura mostra que esse estado é de vapor saturado. é o título da água saindo da turbina.

Agora que entendemos todos os dados que nos foram dados, vamos aprender a calcular próxima etapa.
Passo 2
Para a gente conseguir encontrar a vazão de água quente , a gente precisa primeiro calcular . é calculado através da primeira lei para regime permanente aplicada à turbina. A corrente de água está entrando na turbina e a corrente de água está saindo dela. A equação da primeira lei se encontra abaixo.
Como a turbina está em regime permanente, toda massa que entra tem que sair. Por isso, a vazão de água que entra é igual à vazão de água que sai .
A fórmula acima mostra que para calcular , precisamos encontrar os valores das entalpias específicas e . Por isso, no próximo passo vamos aprender a calcular esses valores.
Passo 3
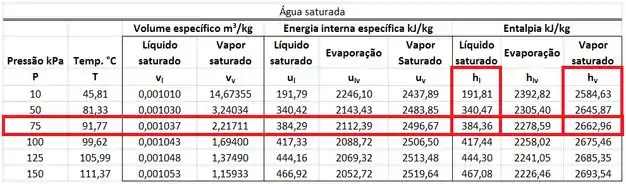
O valor de pode ser encontrado na tabela de saturação da água. Ele está na mesma linha que a pressão de e na mesma coluna que a entalpia específica do vapor saturado .
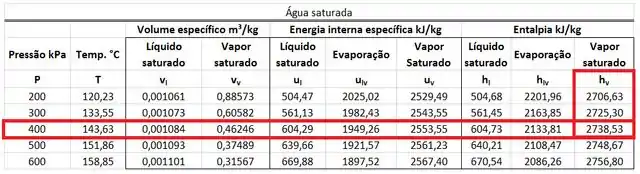
O valor de também pode ser encontrado na tabela de saturação da água. Ele é uma mistura entre a entalpia específica do líquido saturado a e a entalpia específica do vapor saturado a . A fórmula dele se encontra abaixo.
está na mesma linha que a pressão de na mesma coluna que da tabela. está na mesma linha que a pressão de na mesma coluna que da tabela.
O próximo passo é a primeira etapa para aprender a calcular a vazão mássica de água quente que a questão pede.
Passo 4
Para descobrir quanto vale temos que descobrir quanto vale o título da água que sai da restrição. Faremos isso agora!

A figura da questão mostra que a água que sai da restrição é uma mistura de líquido saturada a e vapor saturado a . Por isso, a entalpia dessa corrente de água é uma mistura entre a entalpia específica do líquido saturado a e a entalpia específica do vapor saturado a . A fórmula dessa entalpia está abaixo.
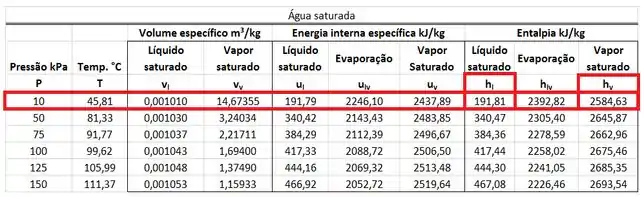
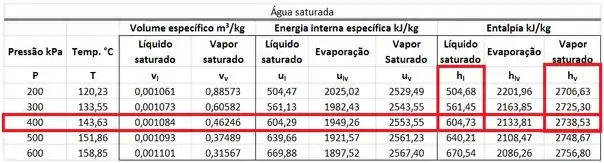
está na mesma linha que a pressão de na mesma coluna que da tabela de saturação. está na mesma linha que a pressão de na mesma coluna que da tabela de saturação.
Se a gente reorganizar essa equação, a gente consegue criar uma fórmula para o título .
A gente consegue encontrar a entalpia específica aplicando a equação da primeira lei na restrição. Essa equação diz que é igual à entalpia específica da corrente de água quente.
A corrente de água é um líquido comprimido porque a sua pressão é maior que a pressão de saturação a . Por isso, a gente teria que ver o valor da entalpia específica dessa corrente na tabela de líquido comprimido. No entanto, geralmente não temos tabelas de líquido comprimido para uma pressão tão baixa.

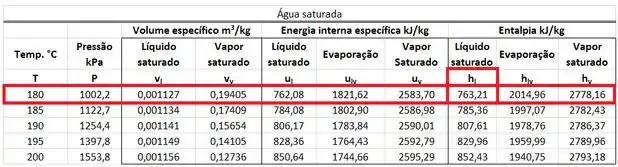
Para resolver esse problema, podemos considerar igual a entalpia de líquido saturado a . Esse valor está na mesma linha que a temperatura de e na mesma coluna que .
Agora que aprendemos a calcular o título da água que sai da restrição, vamos para a útlima etapa de cálculo de .
Passo 5
pode ser calculado de outro jeito. Saber isso é fundamental para calcular . é a massa de vapor d’água presente na corrente dividida pela massa total de água presente na corrente. A massa de vapor que escoa a cada segundo pela saída da restrição é igual à vazão . A massa total que escoa pela saída da restrição a cada segundo é igual à . Logo, é igual a:
Reorgazinando essa fórmula, encontramos uma fórmula para .
Depois de entender tudo isso, podemos iniciar as contas!
Passo 6
Primeiro vamos determinar quanto vale .
Com esse valor, podemos achar . Mas ates temos que converter a unidade de de para .
O próximo passo é achar o valor de .
Por fim, podemos calcular .
Ainda não acabou! O enunciado pede que a gente dê o resultado em . Para converter de para , temos que multiplicar por .