Entalpia, Energia Interna e Calores Específicos de Gases Perfeitos
Teoria
Como calcular a variação de energia de gases perfeitos?
A fórmula abaixo é conhecida como a primeira lei da termodinâmica para processos de sistemas fechados. Ela é muito importante para vários exercícios de termodinâmica, porque ela mostra que a variação de energia do sistema é igual à energia trocada por trabalho e calor .
Ou seja, se nós sabemos quanto vale e , conseguimos calcular a variação de energia do sistema pela fórmula acima. Se conhecemos e , somos capazes de calcular . Por fim, se o enunciado nos dá os valores de e , podemos calcular .
O problema é que nem sempre o enunciado informa diretamente quanto vale a variação de energia do sistema . As vezes ele nos dá de uma forma indireta. Por exemplo, ele pode nos dar a variação de altitude do sistema ou as velocidades e . Aí vamos precisar calcular pela fórmula abaixo.
Se soubermos apenas quanto vale , e , faltará saber quanto vale a variação de energia interna específica do sistema ! Normalmente, achamos através das tabelas termodinâmicas! Mas e se o sistema for formado por um gás perfeito? Como podemos conhecer , se não existem tabelas termodinâmicas de gases perfeitos?
Nós podemos descobrir através de informações sobre os calores específicos e do gás!
Calores específicos de gás perfeito
Para falar sobre os calores específicos, precisamos lembrar da fórmula de calor específico para uma substância simples compressível!
O calor específico a volume constante foi definido como a derivada parcial da energia interna específica, mantendo o volume específico constante.
Já o calor específico a pressão constante foi definido como a derivada parcial da entalpia específica, mantendo a pressão constante.
Note que essas duas fórmulas de substâncias simples compressíveis têm derivadas parciais! Isso acontece, porque a energia interna específica e a entalpia específica dependem de três variáveis: a temperatura , a pressão e o volume específico . Ou seja, se o valor de uma dessas três variáveis mudar, o valor de e mudam.
Para gases perfeitos, a energia interna específica e a entalpia específica só variam com a temperatura! Isso quer dizer que, se os valores de e mudarem, os valores de e permanecem constantes! Como e de gases perfeitos dependem de apenas uma variável, suas derivadas são ordinárias!
onde:
- é o calor específico a volume constante do gás perfeito. Sua unidade no Sistema Internacional (S.I.) é o joule por quilograma-kelvin ;
- é o calor específico a pressão constante do gás perfeito. Sua unidade no Sistema Internacional (S.I.) é o joule por quilograma-kelvin .
Isso simplifica as equações dos calores específicos! Agora sabemos que os calores específicos de gases perfeitos só dependem da temperatura do gás. Mas de que forma podemos usar essa simplificação da derivada para calcular de gases perfeitos?
Veremos isso agora!
Como calcular a partir dos calores específicos ( e )?
Para calcular o que queremos, precisamos reorganizar as equações de e .
Se a gente integrar essas duas equações do estado 1 (antes do sistema passar pelo processo) até o estado 2 (depois do sistema passar pelo processo), chegamos nas seguintes equações:
Mas como podemos resolver essas integrais se ainda não tivemos nenhuma informação de como os calores específicos e variam com a temperatura ?
Existem três formas de resolver essa integral! A escolha de qual forma devemos usar depende de qual aproximação vamos aplicar na questão e de qual informação temos a disposição!
- Se o exercício disser que os calores específicos são constantes, as integrais viram:
- Podemos encontrar os valores de e em uma tabela com valores de calor específico para gases perfeitos a temperatura ambiente. Mas essa solução é a aproximação menos precisa.
- Caso a gente tenha a disposição uma equação para ou em função da temperatura, podemos integrar normalmente. Essa é uma solução mais precisa!
- A terceira forma evita o cálculo da integral. Alguns exercícios nos dão diretamente tabelas com os valores de entalpia específica para diversas temperaturas . Essa é a solução mais precisa de todas!
A explicação mais detalhada de como devemos usar as tabelas será feita a seguir!
Como calcular , considerando os calores específicos ( e ) constantes?
Caso o enunciado do problema diga que os calores específicos são constantes, você provavelmente vai ter acesso a uma tabela parecida com a mostrada abaixo.
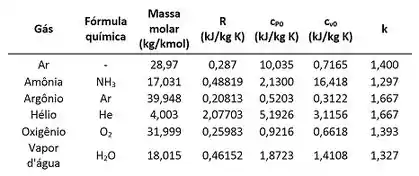
Para descobrir quanto vale , temos que substituir o valor de da tabela nas fórmulas mostradas na primeira forma de resolver a integral.
Mas, tenha atenção! Nem sempre o enunciado vai te falar diretamente que é para considerar os calores específicos como constantes! As vezes você terá que lembrar do gráfico abaixo!
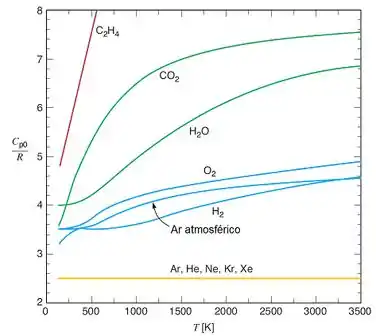
Esse gráfico mostra que o calor específico de gases com apenas um átomo nas suas moléculas é praticamente constante! Chamamos esses gases de gases monoatômicos. Alguns exemplos de gases monoatômicos são:
Ou seja, quando o enunciado faz questão de te informar que o gás do exercício é monoatômico, ele está querendo te dizer, de um jeito indireto, que seus calores específicos são constantes!
Razão de calores específicos
Na tabela de calores específicos acima vemos que existe uma variável . Qual é o significado dela?
O da tabela é uma propriedade termodinâmica chamada de razão de calores específicos. Atenção! Não é só o gás perfeito que possui essa propriedade! Todas as substâncias possuem esses dois calores específicos! Logo, todas elas possuem essa propriedade . Ela tem esse nome, porque ela é o dividido pelo .
Como calcular , quando temos equações para e ?
Geralmente, as tabelas com as equações de calor específico nos dão apenas uma equação de . Ou seja, com essa informação conseguimos somente calcular ! A fórmula de é, na maioria das vezes, um polinômio como o mostrado abaixo.
onde:
- é o calor específico do gás perfeito em quilojoule por quilograma-kelvin ;
- , , e são as constantes do polinômio;
- é a temperatura em kelvin dividida por mil.
O valor das constantes aparecem em tabelas parecidas com a tabela abaixo.
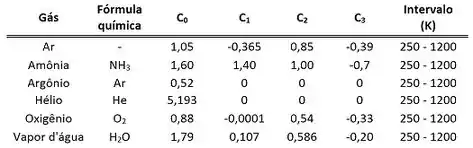
E como podemos calcular se a tabela só possui uma fórmula para ?
Fazemos isso, calculando através de !
Calculando em função de
Para criar uma equação de em função de , precisamos usar uma formulazinha muito tranquila que relaciona o calor específico a volume constante do gás perfeito com o calor específico a pressão constante do gás perfeito .
Agora é só substituir a equação de na expressão abaixo para encontrar uma fórmula de que possa ser integrada para achar !
Vamos ver a terceira e última forma de calcular ? Bora!
Como calcular com tabelas de entalpia específica ?
As tabelas de entalpia específica são muito parecidas com a tabela abaixo para oxigênio .
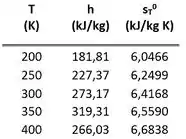
O presente na tabela é uma variável que não nos interessa agora! Vamos focar só em !
Como podemos usar as informações dessa tabela para resolver exercícios de primeira lei, se a tabela só nos dá valores de e a equação de primeira lei só quer valores de ?
Reorganizando a fórmula de entalpia específica para gases perfeitos!
Agora é só substituir o valor de da tabela na equação acima para achar !
Como calcular u 2 - u 1 a partir dos calores específicos ( c P 0 e c v 0 )?
Como calcular u 2 - u 1 , considerando os calores específicos ( c P 0 e c v 0 ) constantes?
Razão de calores específicos k
Como calcular u 2 - u 1 , quando temos equações para c P 0 e c v 0 ?
Calculando c v 0 em função de c P 0
Como calcular u 2 - u 1 com tabelas de entalpia específica h ?
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Um cilindro-pistão isolado termicamente contendo de ar sofre um trabalho de compressão de . Considerando o calor específico do ar constante, calcule a variação da temperatura do ar com esse processo. Utilize a tabela abaixo.
Passo 1
Tudo joinha, pessoas? Vamos direto ao ponto e descobrir como usar o calor específico de um gás perfeito pra calcular a variação de temperatura do gás?
Esse exercício quer saber quanto vale a variação de temperatura do ar , quando ele é comprimido! A figura abaixo mostra os dados que temos pra calcular .
é a energia interna do ar antes de ser comprimido e é a energia interna do ar depois de ser comprimido. é o trabalho de compressão. Ele é negativo, porque o ar está recebendo energia com a compressão. é o calor trocado entre o ar e o ambiente. vale zero, porque o conjunto cilindro pistão é isolado termicamente. Aplicando a primeira lei no ar, encontramos:
Usando essa equação, somos capazes de achar a variação de energia interna . Conhecer quanto vale é fundamental pra achar . A equação de gases ideais abaixo mostra a relação entre e pra gases com calor específico constante.
onde é o calor específico a volume constante do ar que vale .
Com todas essas informações em mãos, estamos aptos a achar no próximo passo.
Passo 2
O primeiro passo pra achar é achar , reorganizando a primeira lei da termodinâmica.
Substituindo o valor de , na fórmula de :
Que ótimo! Já achamos o resultado que o enunciado pediu!
Resposta
Exercício Resolvido #2
Elaboração própria
Um tanque rígido contendo de dióxido de carbono recebe de calor. Utilizando um polinômio para calcular o calor específico do determine a variação da temperatura do com esse processo. Suponha que o calor específico do é constante e é igual ao calor específico avaliado na temperatura de . Utilize as tabelas abaixo.
Passo 1
Tudo tranquilo, gente? Vamos direto ao ponto e descobrir como usar o calor específico de um gás perfeito pra calcular a variação de temperatura do gás?
Esse exercício quer saber quanto vale a variação de temperatura do , quando ele recebe de calor! A figura abaixo mostra os dados que temos pra calcular .
é a energia interna do antes de ser aquecido e é a energia interna do depois de ser aquecido. é o calor trocado entre o ar e o ambiente.
O primeiro passo pra achar , é aplicar a primeira lei no tanque rígido.
Para usar essa equação, precisamos lembrar que o trabalho vale zero, porque o tanque não permite a variação de volume do gás.
Usando a primeira lei, somos capazes de achar a variação de energia interna . Conhecer quanto vale é fundamental pra achar . A equação de gases ideais abaixo mostra a relação entre e pra gases com calor específico constante.
onde é o calor específico a volume constante do que será encontrada a partir da equação presente em uma tabela.
Com todas essas informações em mãos, estamos aptos a achar no próximo passo.
Passo 2
A primeira etapa passo pra calcular é achar , reorganizando a primeira lei da termodinâmica.
Agora só falta achar pra calcular .
Passo 3
Para achar o valor de , temos que usar a equação de fornecida por uma tabela. Essa fórmula nos dá os valores de para qualquer valor da temperatura do gás. O enunciado pede para a gente usar o calor específico da temperatura de .
Para achar a partir do da tabela, usamos a equação de gases perfeitos abaixo.
onde é a constante de gás do que vale .
é calculado através da equação abaixo.
onde é a temperatura que usamos pra calcular dividida por . Logo, é:
Os coeficientes , , e estão presentes na tabela abaixo.
Substituindo esses valores na equação de :
Usando a equação que calcula a partir de :
Agora estamos aptos a achar !
Passo 4
Substituindo os valores de e , na fórmula de :
Que ótimo! Já achamos o resultado que o enunciado pediu!
Resposta
Exercício Resolvido #3
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 129-5.83
Determine a variação de energia interna específica para o quando este é aquecido de a utilizando:
- o valor de da Tab. A.5
- o valor de avaliado com a equação presente na Tab. A.6 e na temperatura média do intervalo.
- Os valores de apresentados na Tab. A.8
Passo 1
Fala, galera! Vamos fazer esse exercício para entender como se usa o calor específico a volume constante no cálculo da variação de energia interna específica ?
O exercício quer que a gente calcule a variação de energia interna , quando o aumenta sua temperatura de até ! Pra achar de um gás perfeito através de , usamos sempre a integral abaixo.
A questão quer que a gente ache o valor de , usando dois valores de diferentes obtidos nas duas tabelas (Tab. A.5 e Tab. A.6) e usando os valores de entalpia da Tab. A.8.
Primeiro, a questão quer que a gente ache , considerando o valor de constante e igual ao valor presente na tabela A.5. Sabendo disso, já podemos achar no próximo passo!
Passo 2
O primeiro jeito de encontrar o valor de é achar o valor de na tabela abaixo e substituir esse valor na integral do passo 1.
Através dessa tabela, vemos que o calor específico a volume constante do vale:
Substituindo esse valor na integral ela vira:
Colocando a constante pra fora da integral e integrando , achamos:
Aeeee! A letra (a) da questão já foi resolvida. Agora vamos encontrar da segunda forma!
Passo 3
Para encontrar da segunda forma, temos que achar o valor de através da equação de fornecida pela tabela A.6. Essa fórmula nos dá os valores de para qualquer valor da temperatura do gás. Como o valor da temperatura de varia de a , o enunciado pede para a gente usar o calor específico da temperatura média na integral.
Para achar a partir do da tabela, usamos a equação de gases perfeitos abaixo.
onde é a constante de gás do e é encontrada na tabela anterior. Ela vale .
é calculado através da equação abaixo.
onde é a temperatura que usamos pra calcular dividida por . Logo, é:
No próximo passo acharemos , , e através da tabela A.6, para achar da segunda forma.
Passo 4
Os coeficientes , , e estão presentes na tabela abaixo.
Substituindo esses valores na equação de :
Usando a equação que calcula a partir de :
Para encontrar , substituímos esse valor de na integral do passo 1, colocamos a constante pra fora e integramos .
Resolvemos a letra (b)! Então vamos tentar resolver a letra (c), calculando da terceira forma!
Passo 5
Pra calcular a variação de energia interna da terceira forma, temos que encontrar o valor da energia interna que o tinha e o valor de energia interna que o passou a ter depois de aumentar sua temperatura.
Pra encontrar e , usamos os valores da entalpia que o tinha quando sua temperatura media e da entalpia que o passou a ter quando sua temperatura passou a medir . e estão presentes na tabela abaixo.
Pra encontrar e a partir de e , usamos as fórmulas que servem apenas para gases perfeitos encontradas abaixo:
Substituindo os dados que temos:
Com e somos, enfim, capazes de achar :
Com a resposta da letra (c) encerramos esse exercício! Ele te ajudou a fixar o conteúdo da teoria? Responde aí!
Resposta
Exercício Resolvido #4
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 130-5.89(a)
Um tanque rígido com volume interno igual a contém gás metano a e . O tanque é, então, resfriado até . Determine a massa de metano contida no tanque e o calor transferido no processo utilizando as tabelas de gás perfeito. Use a tabela abaixo.
Passo 1
Oi, gente! Esse é um exercício que pede pra gente calcular a massa de metano contida no tanque e o calor trocado entre metano do tanque e o ambiente.
Para calcular o calor trocado entre o tanque e o ambiente durante o processo que resfria o metano da temperatura até a temperatura , usamos a primeira lei.
onde é a energia interna do metano depois de ser resfriado a e é a energia interna do metano a e pressão . é o trabalho de movimento de fronteira que o metano realiza sobre o ambiente. Como o tanque é rígido, não tem como o metano mudar seu volume e movimentar suas fronteiras. Logo, o trabalho vale zero!
Pela fórmula de , vemos que precisamos achar a massa de metano primeiro, pra encontrar depois. Achamos essa massa , aplicando a equação dos gases perfeitos no metano que ainda não foi resfriado.
onde é a constante de gás do metano que vale e é o volume do tanque que vale .
Como já temos todos os dados necessários, vamos calcular a massa de metano no próximo passo.
Passo 2
Antes de usar a fórmula de , precisamos converter o volume de pra , dividindo por !
Substituindo esse valor na fórmula de :
Pronto, já achamos uma informação que o enunciado pediu.
Agora, só precisamos aprender a calcular a diferença de energia interna pra conseguir calcular o calor . Faremos isso no próximo passo!
Passo 3
Pra achar a diferença entre energias internas , podemos usar a fórmula de diferença de energia interna dos gases perfeitos com calor específico constante.
onde é o calor específico a volume constante do metano que vale segundo a tabela de gases perfeitos abaixo.
Substituindo , e na equação de , encontramos:
Usando esse valor, podemos achar quanto vale .
Aeeeee! Achamos o calor trocado que a questão pedia pra gente! Acabamos com esse exercício!
Resposta
Exercício Resolvido #5
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 129-5.85
Inicialmente, a água de uma amostra se encontra a e . A água é então aquecida até que o estado onde a temperatura e a pressão são iguais a e . Determine a variação de energia interna no processo utilizando as tabelas de propriedades termodinâmicas da água e as tabelas de gás perfeito.
Passo 1
Oi, gente, partiu fazer esse exercício de cálculo de variação de energia interna específica da água?
Esse exercício quer saber o da água, quando água líquida a e com energia interna específica é aquecida até virar um vapor muito superaquecido (também chamado de gás) a , e energia interna específica .
Como a água que tem energia interna é líquida, não devemos usar as tabelas de gás perfeito pra achar . Achamos através das tabelas de propriedades termodinâmicas! No entanto, não podemos usar essa tabela pra achar , porque a temperatura é maior que a temperatura de vapor presente na tabela. No próximo passo resolveremos isso!
Passo 2
Já sabemos onde encontrar , mas como achamos a energia interna específica do vapor superaquecido a , se não existe informações do vapor a essa temperatura na tabela de propriedades da água?
Pra contornar esse problema, temos que dividir o cálculo de no cálculo de e .
é a variação de energia interna que a água tem, quando vai de , e a , e . é a energia interna do vapor que conseguimos obter através da tabela da água! Ou seja, é a variação de energia interna da água que a gente consegue calcular usando apenas as tabelas de propriedades da água.
é a variação de energia interna da água que podemos calcular usando apenas a tabela de gás perfeito de . Ou seja, é a variação da energia interna do gás perfeito de água, quando ele vai de e a e . é a energia interna específica do gás obtida na tabela de gás perfeito. Por isso, é diferente de .
No próximo passo nós vamos achar e na tabela termodinâmica da água e calcular !
Passo 3
Primeiro, encontramos a energia interna da água líquida comprimida a e . Como não tem tabela pra água líquida comprimida a essa pressão e temperatura, usaremos a energia interna da água líquida saturada a obtida da tabela abaixo.
é um vapor superaquecido a e . Logo, achamos a partir da tabela de vapor superaquecido nessa temperatura e pressão.
Substituindo e na equação de , achamos:
Boa! Calculamos a primeira parte de . Então vamos partir para o cálculo de no próximo passo para conseguir calcular !
Passo 4
Pra calcular , temos que encontrar o valor das energias internas e usamos os valores da entalpia de a e da entalpia de a presentes na tabela de gás perfeito de . Para achar e , temos primeiro que converter as unidades das temperaturas e de pra .
Não conseguimos encontrar os valores de entalpia pra essas temperaturas através da tabela de gases perfeitos que temos. Por isso, teremos que interpolar os valores de entalpia!
Pra encontrar e a partir de e , usamos as fórmulas que servem apenas para gases perfeitos encontradas abaixo:
onde é a constante de gás da água que vale .
Substituindo os dados que temos:
Com e somos, enfim, capazes de achar :
Somando com , achamos !
Aeeee! Foi sofrido, mas achamos o que o enunciado pediu! Pra isso, tivemos que dividir o em uma parcela que era encontrada nas tabelas de propriedades e em outra parcela que era obtida nas tabelas de gases perfeitos. mas apesar do trabalho deu tudo certo! :)
Resposta
Exercício Resolvido #6
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 129-5.87
Um quilograma de deve ser aquecido de a a pressão de . Calcule a variação de entalpia específica neste processo com os seguintes métodos:
- Calor específico constante e com valor tomado na Tab A.5.
- Calor específico constante mas avaliado com a equação da Tab. A.6 e a temperatura média.
- Calor específico variável e integrando a equação da Tab. A.6.
- Utilizando as tabelas de gases perfeitos (A.8).
Passo 1
Fala, galera! Bora fazer esse exercício para entender como se usa o calor específico a pressão constante no cálculo da variação de entalpia ?
O exercício quer que a gente calcule a variação de entalpia de de , quando o aumenta sua temperatura de até ! Pra achar de um gás perfeito através de , usamos sempre a integral abaixo.
A questão quer que a gente ache o valor de , usando três valores de diferentes obtidos em duas tabelas (Tab. A.5 e Tab. A.6) e usando os valores de entalpia da Tab. A.8.
Primeiro, a questão quer que a gente ache , considerando o valor de constante e igual ao valor presente na tabela A.5. Sabendo disso, já podemos achar no próximo passo!
Passo 2
O primeiro jeito de encontrar o valor de é achar o valor de na tabela abaixo e substituir esse valor na integral do passo 1.
Através dessa tabela, vemos que o calor específico a volume constante do vale:
Substituindo esse valor na integral ela vira:
Colocando a constante pra fora da integral e integrando , achamos:
Aeeee! A letra (a) da questão já foi resolvida. Agora vamos encontrar da segunda forma!
Passo 3
Para encontrar da segunda forma, temos que achar o valor de através da equação de fornecida pela tabela A.6. Essa fórmula nos dá os valores de para qualquer valor da temperatura do gás. No entanto, o enunciado pede para, primeiramente, a gente usar o calor específico da temperatura média na integral.
é calculado através da equação abaixo.
onde é a temperatura que usamos pra calcular dividida por . Logo, é:
No próximo passo acharemos , , e através da tabela A.6, para achar da segunda forma.
Passo 4
Os coeficientes , , e estão presentes na tabela abaixo.
Substituindo esses valores na equação de :
Para encontrar , substituímos esse valor de na integral do passo 1, colocamos a constante pra fora e integramos .
Resolvemos a letra (b)! Então vamos tentar resolver a letra (c), calculando da terceira forma!
Passo 5
Uma terceira forma de calcular a variação de entalpia , é substituindo a expressão de do passo 3 na integral de , usando os coeficientes , , e que achamos no passo 4.
Substituindo os coeficientes , , e que achamos no passo 4:
Achamos a resposta da letra (c) e estamos na reta final da questão! Vamos pro último passo!
Passo 6
Na última forma de calcular a variação de entalpia , temos que encontrar o valor da entalpia que o tinha e o valor de entalpia que o passou a ter depois de aumentar sua temperatura.
Pra encontrar e , usamos os valores da entalpia que o tinha quando sua temperatura era de e da entalpia que o passou a ter quando sua temperatura passou a medir . e são calculados a partir das entalpias da tabela abaixo por interpolação.
Com e somos, enfim, capazes de achar .
Com a resposta da letra (d) encerramos esse exercício! Ele te ajudou a fixar o conteúdo da teoria? Responde aí!
Resposta
Exercício Resolvido #7
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 129-5.86
Nós precisamos determinar o aumento de temperatura de uma amostra de gás nitrogênio que inicialmente apresentatemperatura igual a . Sabendo que o aumento de energia interna específica do nitrogênio é , determine a variação de temperatura ocorrida utilizando:
- o valor de da Tab. A.5
- o valor de avaliado com a equação presente na Tab. A.6 e na temperatura igual a .
- Os valores de apresentados na Tab. A.8
Passo 1
Fala, galera! Vamos fazer esse exercício para entender como se usa o calor específico a volume constante no cálculo da variação de temperatura de um gás?
O exercício quer que a gente calcule a variação de temperatura do gás , quando a variação de energia interna específica do gás vale ! Pra achar de um gás perfeito, assumindo que é constante, usamos sempre a equação abaixo.
A questão quer que a gente ache o valor de , usando dois valores de diferentes obtidos nas duas tabelas (Tab. A.5 e Tab. A.6) e usando os valores de entalpia da Tab. A.8.
Primeiro, a questão quer que a gente ache , considerando o valor de constante e igual ao valor presente na tabela A.5. Sabendo disso, já podemos achar no próximo passo!
Passo 2
O primeiro jeito de encontrar o valor de é achar o valor de na tabela abaixo e substituir esse valor na equação do passo 1.
Através dessa tabela, vemos que o calor específico a volume constante de vale:
Substituindo esse valor na equação de :
Aeeee! A letra (a) da questão já foi resolvida. Agora vamos encontrar da segunda forma!
Passo 3
Para encontrar da segunda forma, temos que achar o valor de através da equação de fornecida pela tabela A.6. O enunciado pede para a gente usar o calor específico na temperatura na equação de . Para achar a partir do da tabela, usamos a equação de gases perfeitos abaixo.
onde é a constante de gás do e é encontrada na tabela anterior. Ela vale .
é calculado através da equação abaixo.
onde é a temperatura que usamos pra calcular dividida por . Logo, é:
No próximo passo acharemos , , e através da tabela A.6, para achar da segunda forma.
Passo 4
Os coeficientes , , e estão presentes na tabela abaixo.
Substituindo esses valores na equação de :
Usando a equação que calcula a partir de :
Para encontrar , substituímos esse valor de na equação do passo 1.
Resolvemos a letra (b)! Então vamos tentar resolver a letra (c), calculando da terceira forma!
Passo 5
Pra calcular a variação de temperatura da terceira forma, temos que encontrar primeiro o valor da energia interna que o tinha, quando sua temperatura valia e o valor de energia interna que o passou a ter depois de aumentar sua energia interna em .
Pra encontrar , usamos o valor da entalpia que o tinha quando sua temperatura media . está presente na tabela abaixo.
Pra encontrar a partir de , usamos a fórmula que serve apenas para gases perfeitos abaixo.
Substituindo os dados que temos na equação de :
Agora, temos que encontrar a partir de para usar a tabela de gases perfeitos e encontrar a temperatura que o gás passa a ter após o aumento na energia interna! Achamos a partir da equação que serve para gases perfeitos encontrada abaixo.
Como vimos na letra (a) e (b) da questão, o aumento de temperatura deve ser menor que . Logo, deve ficar entre e . Isso quer dizer que podemos achar interpolando a tabela de entalpia pra gases perfeitos.
Igualando essa equação de a outra equação de , podemos achar o valor de .
Reorganizando essa equação:
Subtraindo de , achamos .
Com a resposta da letra (c) encerramos esse exercício! Show!!!
Resposta
Exercício Resolvido #8
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 130-5.90
Um tanque rígido e isolado termicamente está dividido em duas regiões por meio de uma membrana (veja o esboço da Fig. P5.58). A região apresenta e contém ar a e . A região apresenta e contém ar a e . A membrana é, então, rompida e espera-se que seja estabelecido o equilíbrio. Determine a pressão e a temperatura do ar no estado final deste processo. Use as tabelas abaixo.
Passo 1
E aí, querid@s! Indo direto ao ponto, esse exercício quer saber quanto valem a pressão e a temperatura do ar, depois da membrana furar e permitir que o ar das regiões e se misturem. A figura abaixo mostra os dados que temos pra calcular e .
Como o tanque com ar está isolado termicamente, a troca de calor entre o ar e o ambiente vale zero.
Além disso, o trabalho realizado pela ar no ambiente vale zero, porque a mistura de ar é apenas uma expansão não resistida.
Essas duas informações são muito importantes! Usando esses novos dados na equação de conservação de energia, descobrimos quanto vale a energia interna específica do ar misturado! Saber quanto vale é fundamental pra achar a temperatura do ar misturado (que é uma incógnita do problema) através da tabela de gases perfeitos.
onde é a energia interna do ar misturado e é a soma da energia interna da região com a energia intern da região .
No entanto, a energia interna é sempre a massa multiplicada pela energia interna por unidade de massa .
Agora que temos uma fórmula pra achar , podemos começar a encontrar as variáveis , , , e que são necessárias para acharmos . No próximo passo a gente vai iniciar as contas, encontrando , e .
Passo 2
Para achar a massa de ar da região , usamos a equação de gases perfeitos abaixo.
onde é a constante de gás do ar que vale .
Substituindo esse valor na fórmula de :
Também temos que usar a equação de gases perfeitos pra descobrir a massa da região .
A massa de ar misturado é a soma das massas e que o ar tinha antes de se misturar.
Agora só falta encontrar e através das tabelas de gás perfetio na próxima etapa pra poder achar .
Passo 3
Para achar e , vamos precisar usar a tabela de gás perfeito do ar abaixo.
Substituindo esss dois valores na fórmula de :
Como vocês podem ver pela tabela de gás perfeito do ar abaixo, a energia interna é correspondente a uma temperatura que está entre e . Logo, faremos uma interpolação pra achar a temperatura através dessa tabela.
Que beleza! Encontramos uma das informações que o enunciado pedir! Agora só falta encontrar no próximo passo!
Passo 4
Para encontrar a pressão do ar misturado, usaremos a equação de gás perfeito para o ar misturado.
Pronto, achamos a pressão e fechamos o exercício! Uhuuuul!