Calores Específicos
Teoria
O que é calor específico ?
Para esquentar de vapor d’água em , ela precisa receber de energia. Para esquentar de amônia líquida em , ela precisa receber de energia. Por que o vapor d’água precisa absorver mais energia que a amônia líquida, se a variação de temperatura das duas é igual?
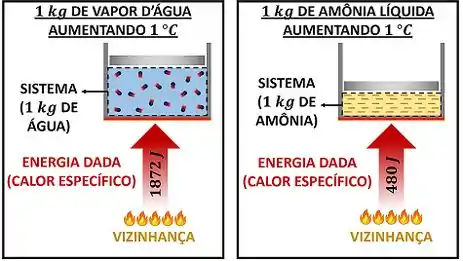
Porque o calor específico do vapor d’água é maior que o calor específico da amônia líquida! O calor específico é a quantidade de energia que um quilograma da substância precisa absorver pra conseguir aumentar sua temperatura em . Quanto maior o seu valor, mais energia a substância tem que absorver! Por exemplo:
onde:
- é o calor específico do vapor d’água. A unidade do calor específico, de acordo com o Sistema Internacional de Unidades (S.I.), é o joule por quilograma por kelvin . A unidade joule por quilograma por grau Celsius é igual a !
- é o calor específico da amônia líquida. Nas tabelas termodinâmicas, a unidade do calor específico está em quilojoule por quilograma por kelvin , mas é fácil converter essa unidade para a unidade em S.I.
- o calor trocado;
- a massa do sistema;
- a energia interna específica do sistema depois dele ganhar mais de temperatura;
- a energia interna específica do sistema antes dele trocar energia.
Existe mais de um tipo de calor específico?
Existem dois tipos de calor específico. O primeiro tipo é a energia que da substância precisa receber para aumentar , sem deixar o seu volume mudar. O segundo tipo é a energia que da substância precisa receber para aumentar , sem deixar a sua pressão mudar.
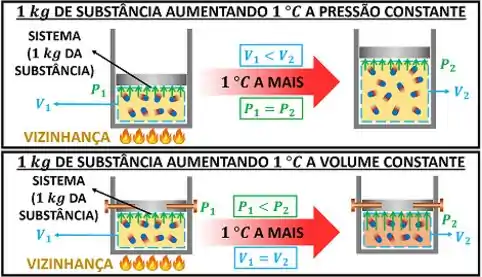
Nos dois casos, nós queremos conhecer a quantidade de energia trocada entre o sistema e a sua vizinhança. A primeira lei da termodinâmica serve, justamente, para calcular a troca de energia entre os dois. Então por que não usamos a primeira lei para fazer as contas?
Calor específico a volume constante
Ótima ideia! Vamos começar, usando a primeira lei para calcular a energia que o sistema recebe, sem variar seu volume. Ou seja, vamos calcular a energia que da substância precisa absorver para variar da sua temperatura, mantendo o seu volume constante.
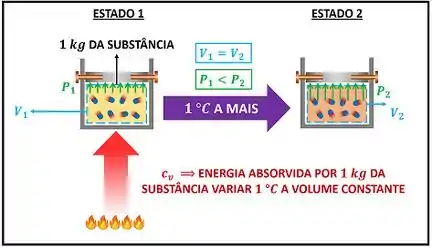
Para facilitar nossas contas, vamos supor que a velocidade do sistema não varia e que a altura do sistema também não muda. Além disso, vamos considerar que o sistema só recebe energia por calor.
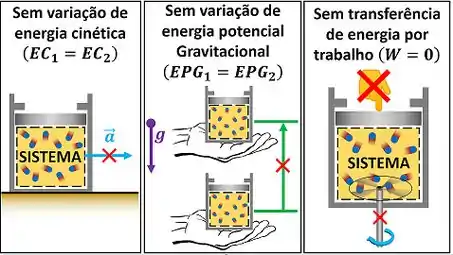
Isso vai simplificar muito os cálculos, porque a equação da primeira lei para esse caso fica menor.
sendo:
Como a massa do sistema vale nesse caso, a equação vira:
Esse resultado é importantíssimo! Ele mostra que a quantidade de energia absorvida pelo sistema é a variação da sua energia interna causada pela variação de temperatura! Dizendo isso de outra forma, esse exemplo nos mostrou que esse primeiro calor específico é igual à taxa de variação da energia interna específica com a temperatura!
Chamamos esse primeiro calor específico de calor específico a volume constante . é a taxa de variação da energia interna específica com a temperatura. O parênteses serve só para reforçar que essa derivação parcial é calculada, mantendo o volume constante.
Agora vamos estudar a segunda forma de se medir o calor específico!
Calor específico a pressão constante
Para calcular esse segundo calor específico, temos que calcular a energia que da substância precisa absorver para variar da sua temperatura, mantendo sua pressão constante. Para facilitar nossas contas, vamos supor de novo que a velocidade do sistema não varia e que a altura do sistema também não muda.
onde é o trabalho realizado pelo sistema.
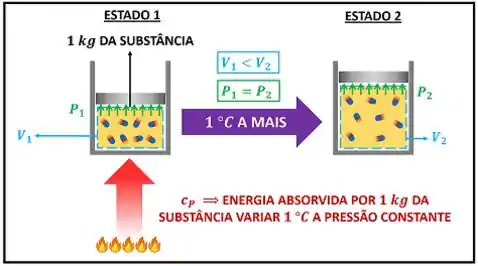
Para manter a pressão do sistema constante, o volume do sistema tem que aumentar. Isso significa que o sistema tem que empurrar o pistão e realizar um trabalho a pressão constante sobre ele. A fórmula do trabalho nesse caso vira:
é a pressão constante do sistema. é o volume do sistema antes dele aumentar de temperatura e é o volume do sistema depois dele receber energia.
Lembrando que o volume é igual ao volume específico vezes a massa do sistema , descobrimos que o trabalho é:
Substituindo a fórmula do trabalho na primeira lei, encontramos que:
Reorganizando a fórmula, chegamos na seguinte equação.
No entanto, a pressão do sistema permanece constante durante todo o processo de absorção de energia. Por causa disso:
Agora é que vem a grande a grande sacada! A combinação entre energia interna, volume e pressão é igual à entalpia!
Como a massa do sistema é igual a
Esse resultado é muito parecido com o resultado de ! Ele mostra que a quantidade de energia absorvida pelo sistema é a variação da sua entalpia causada pela variação de temperatura! Dizendo de outra forma, esse exemplo nos mostrou que esse segundo calor específico é igual à taxa de variação da entalpia específica com a temperatura!
Chamamos esse segundo calor específico de calor específico a pressão constante . é a taxa de variação da entalpia específica com a temperatura. O parênteses serve só para reforçar que essa derivação parcial é calculada, mantendo a pressão constante.
Os calores específicos ( e ) são propriedades intensivas do sistema!
O calor específico a volume constante é calculado a partir de duas propriedades intensivas do sistema ( e ). O calor específico a pressão constante também é calculado a partir de duas propriedades intensivas do sistema ( e ). Isso quer dizer que e também são propriedades intensivas do sistema? Sim! Acertou!
A imagem acima relembra a pergunta que precisamos fazer para descobrir se uma variável é uma propriedade termodinâmica do sistema. Ela é uma propriedade, se conseguimos descobrir o seu valor sem precisar saber o processo que trouxe o sistema até o seu estado. Por isso, não precisamos conhecer a história do sistema para calcular os calores específicos!
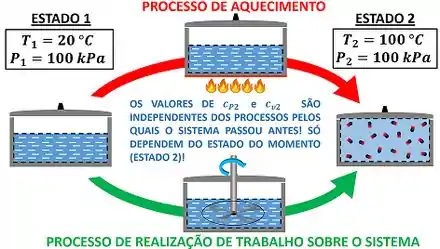
Em outras palavras, os calores específicos não dependem dos detalhes dos processos. Ou seja, apesar de termos chegado na fórmula dos calores específicos fazendo várias simplificações, os resultados obtidos podem ser usados em processos diferentes!
Por exemplo: dois tanques com de vapor d’água a e a recebem energia. Um recebe energia por trabalho. O outro recebe energia por calor. A pressão do sistema permanece constante e a temperatura dos dois sistemas chega a . Qual é o valor de e nesse estado final?
Olhando uma tabela de calores específicos, descobrimos os valores dessas duas propriedades.
e são iguais nos dois casos, porque seus valores só dependem da pressão e da temperatura do sistema! Além disso, o sistema tem um valor de calor específico a volume constante , mesmo tendo passado por um processo de variação do volume! Ou seja, o seu valor não dependeu do tipo de processo pelo qual o sistema passou!
Existe mais de um tipo de calor específico?
Calor específico a volume constante c v
Calor específico a pressão constante c P
Os calores específicos ( c v e c P ) são propriedades intensivas do sistema!
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Suponha que cinco placas de estão sendo aquecidas por uma mesma fonte térmica. Cada placa é constituída de um material: aço, alumínio, gelo, vidro e papel. Considere que esse processo de aquecimento é isobárico. Usando a tabela de calor específico de alguns sólidos abaixo, determine qual placa aumenta de temperatura mais rápido.
Passo 1
O problema quer saber qual das cinco placas de vai esquentar mais rápido! Ou seja, ele que a gente descubra, qual delas vai aumentar sua temperatura em menos tempo.
Sabemos que todas elas têm a mesma massa. Isso quer dizer que, se uma placa variar de temperatura mais rápido, o material dessa placa tem mais facilidade de variar sua temperatura. Isso não pode significar que existe menos material nessa placa, porque todas têm a mesma massa!
Isso também não pode significar que essa placa recebeu mais calor, porque todas as cinco placas estão sendo aquecidas pela mesma fonte térmica!
Sabemos também que o sólido que aumentou sua temperatura em menos tempo precisou receber menos energia para fazer sua temperatura crescer! Ou seja, podemos refazer a pergunta do texto da seguinte forma: qual sólido precisa de menos energia para variar sua temperatura?
Como a gente pode saber disso, se o exercício só nos deu uma tabela com valores de calor específico a pressão constante dos sólidos? Em outras palavras, qual é a ligação entre o calor específico e a quantidade de energia que o material precisa absorver para variar a sua temperatura?
O calor específico é justamente a quantidade de energia que de uma substância precisa absorver para aumentar sua temperatura em . Ou seja, quanto maior o calor específico, maior a quantidade de energia que a substância tem que absorver para aumentar sua temperatura!
Por causa disso, o sólido com menor calor específico também é o sólido que precisa de menos energia para variar sua temperatura!
Então é só ver na tabela qual o sólido com menor valor de calor específico para responder a pergunta da questão! Faremos isso no próximo passo!
Passo 2
Pela tabela, vemos que o aço é o material com menor calor específico.
Em outras palavras, ele precisa de menos energia para aumentar sua temperatura. Por conta disso, ele varia de temperatura mais rápido. Ou seja, a placa feita de aço aumenta de temperatura mais rápido que as outras placas!
Resposta
Placa de aço
Exercício Resolvido #2
Elaboração própria
Um tanque rígido contendo amônia líquida é aquecido até sua temperatura alcançar . Neste estado final, o calor específico a volume constante da amônia mede . Um conjunto cilindro-pistão também contém amônia líquida. Ele realiza trabalho sobre a vizinhança em um processo isobárico. Ao final desse processo, a amônia se encontra no mesmo estado da amônia líquida a presente no tanque rígido. Qual é o calor específico a volume constante da amônia presente no conjunto cilindro-pistão após a realização do trabalho?
Passo 1
Cuidado! Esse exercício é uma grande pegadinha! Ele é perigoso, porque brinca com a interpretação errada mais comum que os estudantes fazem sobre o que é o calor específico! Por conta disso, é necessário corrigir o maior erro de interpretação do calor específico que você pode acabar fazendo: achar que o calor específico não é uma propriedade!
O enunciado fala sobre dois recipientes de amônia líquida: um tanque rígido e um conjunto cilindro-pistão. Os dois líquidos passam por processos diferentes. A amônia do tanque passa por um aquecimento e a amônia do conjunto cilindro-pistão realiza trabalho.
No entanto, mesmo contidas em dois recipientes diferentes e passando por processos diferentes, as duas amônias chegam no mesmo estado final! E o exercício pede o calor específico a volume constante da amônia presente no cilindro nesse estado final! Será que o calor específico final das duas amônias são iguais só porque os estados finais são iguais?
Isso será respondido no próximo passo!
Passo 2
Sim! O calor específico é uma propriedade como qualquer outra! Assim como a temperatura, a pressão e o volume específico, o calor específico só depende do estado da substância! Assim como não precisamos conhecer a história da substância para conseguir medir a sua temperatura em um estado, também não precisamos saber o passado para descobrir o calor específico!
Em outras palavras, não importa de onde a substância partiu nem o caminho que ela percorreu para conhecer o valor do calor específico no estado que queremos!
Por isso, o calor específico a volume constante da amônia no cilindro-pistão é igual ao calor específico da amônia no tanque rígido .
O valor de foi dado no enunciado.
Então:
Resposta
Exercício Resolvido #3
Elaboração própria
Três substâncias estão contidas cada uma em um tanque rígido. Elas são aquecidas, mantendo seus volumes constantes. O gráfico fornece a variação de energia interna específica de três substâncias , e em função da temperatura, conforme elas recebem calor. Calcule, para cada uma das substâncias, o calor específico a volume constante.
Passo 1
O enunciado quer saber quanto valem os de cada substância, mas ele aparentemente só nos fornece um gráfico da energia interna específica de cada substância em função da temperatura. Qual é a ligação entre os e o gráfico? Será que o gráfico é a única informação que o problema nos dá? Não tem nada escondido no texto do enunciado?
A única forma que conhecemos para se calcular o é através da fórmula abaixo.
Ou seja, ele é a derivada parcial da energia interna específica em relação à temperatura, mantendo o volume específico constante. Isso quer dizer que, para descobrir quanto vale , precisamos saber como varia em função de , enquanto permanece constante!
O gráfico nos mostra como varia em função de , mas será que é constante nesse caso?
Para saber se as substâncias estão ganhando energia, mas mantendo seus volumes específicos constantes, temos que descobrir uma informação que está escondida no texto da questão!
A questão nos diz que as três substâncias estão contidas cada uma em um tanque rígido. Isso significa que os seus volumes (, e ) não variam conforme elas são aquecidas!
Além disso, as massas (, e ) das substâncias também não variam durante o aquecimento.
O volume específico é igual ao volume dividido pela massa. Como os dois são constantes, o volume específico também é constante no aquecimento do problema!
Isso mostra que a informação presente no gráfico pode ser usada para calcular os , porque é constante durante o aumento de !
E como podemos calcular a derivada parcial com a ajuda do gráfico?
Isso é o que veremos no próximo passo!
Passo 2
A derivada é a inclinação de uma curva em um determinado ponto.
Vemos pelo gráfico que é uma função linear de . Em outras palavras é uma reta. Ou seja, para calcular os três , temos que calcular a inclinação das três retas , e ! A inclinação dessas retas é igual à variação de dividida pela variação de .
Para achar essa inclinação, precisamos de apenas dois pontos da reta. O ponto 1 (ponto com o valor de menor) e o ponto 2 (ponto com o valor de maior).
Todas as variáveis necessárias para calcular os são obtidas através do gráfico.
Com esses valores nós podemos começar os cálculos.
Deixaremos essa parte para o próximo passo.
Passo 3
Resposta
Exercício Resolvido #4
Elaboração própria
de uma substância contida em um tanque rígido é colocada em contato com uma fonte térmica de fluxo . O gráfico do aquecimento em função do tempo é apresentado. Determine o calor específico a volume constante da substância. Suponha que não exista variações de energias cinética e potencial da substância.
Passo 1
Sabemos que o calor específico a volume constante é a derivada parcial da energia interna específica em relação à temperatura , mantendo o volume específico constante. Ou seja, para calcular o valor de precisamos saber como varia em função de , enquanto permanece constante.
Mas em que parte do enunciado em função de é informado?
A forma que varia com é dada indiretamente pelo enunciado.
Mas antes, para entender como essa informação está escondida no texto do problema, precisamos entender todos os dados que o enunciado mostrou pra gente. Por exemplo, o que é o fluxo de da fonte térmica?
Ele é a quantidade de calor que a substância recebe a cada segundo! Logo, para saber quanto a substância ganha de calor depois de ficar um tempo em contato com a fonte, devemos fazer regra de três! Nós vamos usar o símbolo para representar essa variável em uma fórmula.
onde é o tempo em que o tanque está em contato com a fonte térmica. Ele está em segundos .
O problema diz que:
Mas qual a conexão de com a variação de energia interna específica ?
Descobriremos isso no próximo passo!
Passo 2
Essas duas variáveis se conectam através da primeira lei da termodinâmica!
onde:
- é a variação de energia cinética da substância. Ela vale zero segundo o enunciado;
- é a variação de energia potencial da substância. Ela vale zero segundo o enunciado;
- é a massa da substância. Ela vale segundo o enunciado.
- é o trabalho realizado pela substância;
- é a variação de energia interna específica antes e depois do aquecimento. Ela faz parte da incógnita do problema.
Para descobrirmos , precisamos saber calcular o trabalho . No entanto, o seu valor é dito indiretamente pelo enunciado!
Como o texto não fala nada sobre uma realização trabalho de eixo durante o processo de aquecimento, essa possibilidade é descartada.
Além disso, o texto fala que a substância está contida em um tanque rígido. Isso significa que o volume da substância permanece o mesmo durante todo o aquecimento! Ou seja, não existe movimento de fronteira nem trabalho de movimento de fronteira! Por conta de tudo isso, o trabalho vale:
Depois de todas essas observações, precisamos reorganizar a primeira lei para encontara .
Já descobrimos uma fórmula de em função do tempo , mas, para calcular , precisamos de uma fórmula de em função da variação de temperatura . Como podemos chegar onde queremos?
Isso será mostrado mais pra frente. Antes, temos que ter certeza que a fórmula de conseguimos mostra a variação de para volume específico constante.
Passo 3
Para saber se as substância está ganhando energia, mas mantendo seu volume específico constante, temos que descobrir outra informação que está escondida no texto da questão!
A questão nos diz que a substância está contida em um tanque rígido. Isso significa que o seu volume não varia conforme ela é aquecida! Além disso, a massa () da substância também não varia durante o aquecimento.
O volume específico é igual ao volume dividido pela massa. Como os dois são constantes, o volume específico também é constante no aquecimento do problema!
Isso mostra que a informação presente no gráfico pode ser usada para calcular os , porque é constante durante o aumento de !
Passo 4
Para achar em função de , precisamos descobrir uma fórmula de em função de e depois substituir na fórmula de !
Isso é mostrado no gráfico. Através dele, vemos que em função de é uma reta. Logo, podemos descobrir uma fórmula para essa reta através de dois pontos. O primeiro ponto pode ser o início do aquecimento e o segundo ponto pode ser no tempo de quatro minutos.
A inclinação da reta é constante, logo:
onde:
Reorgazinando a fórmula para , encontramos:
Substituindo essa fórmula na equação de , achamos:
Mas a variação da energia interna específica também pode ser calculada como a diferença entre a energia interna específica durante o aquecimento e a energia interna específica no início do aquecimento .
Substituindo isso na fórmula encontramos que:
Não conhecemos , mas ele é uma constante. Isso quer dizer que esse termo vai desaparecer, quando derivarmos .
Pronto, temos a fórmula de . Então vamos derivá-la no próximo passo para podermos calcular .
Passo 5
Derivando em relação à temperatura , achamos:
Ou seja:
Com isso a gente pode substituir todos os valores que conhecemos e achar .
Passo 6
Resposta
Exercício Resolvido #5
Elaboração própria
Suponha que dois tanques rígidos estão recebendo o mesmo fluxo constante de calor . O tanque contém a substância e o tanque contém a substância . O gráfico abaixo apresenta a evolução da temperatura das substâncias em função do tempo. Qual das duas substâncias possui o maior calor específico a volume constante no momento indicado pela figura?
Passo 1
O enunciado diz que existem duas substância ( e ) dentro de dois tanques rígidos ( e ), recebendo a mesma quantidade de calor por segundo. Essa taxa de calor que cada um deles recebe é igual a . Mas se as duas substâncias recebem a mesma taxa de calor, por que o gráfico de mostra que as temperaturas de e variam com velocidades diferentes?
A resposta para essa pergunta vai ajudar a gente a responder a pergunta do enunciado! e variam suas temperaturas de forma diferente, porque cada substância precisa de uma quantidade diferente de calor para variar a temperatura. Quanto mais energia uma substância precisar absorver para aumentar sua temperatura, mais lento vai ser seu aquecimento.
O oposto também é verdade! Quanto menos energia uma substância precisar absorver para aumentar sua temperatura, mais rápido vai ser seu aquecimento. Por exemplo, a madeira aquece mais devagar do que o metal! Se a gente encontar no metal depois de ele ser aquecido durante um tempo, provavelmente sua mão vai queimar com a temperatura. Isso não ocorreria com a madeira!
Vemos no gráfico do enunciado que a substância varia menos a sua temperatura no instante , porque a inclinação da sua curva de temperatura é menor. Isso quer dizer que sua temperatura está variando de forma mais lenta nesse momento. Ou seja, a substância precisa de mais energia para variar sua temperatura! E o que isso tem a ver com a pergunta do enunciado sobre o calor específico das substâncias e ?
Veremos isso no próximo passo!
Passo 2
O enunciado quer saber qual substância ( ou ) possui o maior calor específico . Mas qual o conexão entre essa pergunta e a discussão que fizemos até aqui?
O calor específico mede a quantidade de energia que uma substância precisa absorver para aumentar sua temperatura!
Quanto maior o calor específico da substância, mais energia ela precisa absorver para aumentar sua temperatura. Isso quer dizer que a substância tem o maior calor específico no momento ! Ela precisa absorver mais energia por calor para variar sua temperatura. Isso torna o seu aquecimento mais lento naquele instante e deixa a sua curva de temperatura com uma inclinação menor!
Resposta
Substância
Exercício Resolvido #6
Elaboração própria
Considere que uma fábrica possui três tanques rígidos. Cada um dos três tanques rígidos contém uma única substância. O tanque contém da substância , o tanque contém da substância e o tanque contém da substância . Os três tanques são aquecidos separadamente. O gráfico fornece a quantidade de calor absorvida pelas três substâncias em função da temperatura. Determine qual é a substância com o menor calor específico a volume constante.
Passo 1
O enunciado fala sobre três tanques rígidos, cada um com uma substância. Eles são aquecidos e a quantidade de calor que as substâncias recebem está mostrada no gráfico. A partir dessas informações a questão pede pra gente calcular o calor específico a volume constante das três substâncias. Os dados e as incógnitas do problema estão ilustrados pela figura abaixo. Depois da figura, será explicado como cada dado foi obtido!
Para conseguir calcular o calor específico a volume constante das três substâncias, precisamos lembrar da única fórmula que temos pra isso. Ela é a derivada parcial da energia interna específica em relação à temperatura , mantendo o volume específico da substância constante.
Para conseguir informações sobre a variação da energia interna específica a volume constante a partir das informações dadas de calor absorvido , temos que utilizar a primeira lei nessas três substâncias (, e ).
O enunciado informa todos os valores de massa.
Ele também diz indiretamente que as substâncias não realizam nem sofrem nenhum trabalho durante o aquecimento. O enunciado faz isso, dizendo que as três substâncias estão em tanques rígidos. Como a parede do tanque não se move, o volume das substâncias não variam. Por causa disso, elas não podem sofrem nem realizar trabalho de movimento de fronteira.
Ou seja, o processo de aquecimento ocorre sem trabalho e a volume constante! A variação de energia interna ocorre a volume constante! Por isso podemos usar os dados do gráfico para utilizar nos cálculos de calor específico a volume constante! Além disso, o gráfico informa o calor absorvido pelas substâncias do ponto 1 até o ponto 2 marcado no gráfico.
Com esses dados, podemos calcular as variações de energia interna específica a volume constante , reorganizando a primeira lei.
Vemos que as variações de energia interna específica dependem da quantidade de calor absorvida . Perceber isso é muito importante, porque a quantidade de calor absorvido varia linearmente. Se a variação de depende de uma quantidade linear , também varia linearmente. Por isso, o calor específico pode ser calculado da seguinte forma.
Vemos pelo gráfico que as temperaturas das substâncias no ponto 1 são iguais a .
Já as temperaturas dos pontos 2 valem:
Com todos esses dados, podemos enfim calcular os calores específicos!
Passo 2
Antes de calcular os calores específicos, temos que calcular a variação de energia interna específica de cada substância.
Com esses valores, podemos encontrar os ’s.
Resposta
A substância
Exercício Resolvido #7
Elaboração própria
Considere que uma fábrica possui dois conjuntos cilindro-pistão. Cada um deles contém uma única substância. O conjunto cilindro-pistão contém da substância e o conjunto cilindro-pistão contém da substância . Os conjuntos cilindro-pistão realizam um processo adiabático de enpansão. O gráfico mostra a quantidade de energia perdida por trabalho pelas duas substâncias em função da temperatura. Suponha que o processo de expansão das substâncias e é isobárico a de pressão. Determine o calor específico a pressão constante das duas substâncias.
Passo 1
O enunciado fala sobre dois cilindros-pistões e , cada um com uma substância. Eles realizam trabalho. A quantidade de trabalho que as substâncias realizam está mostrada no gráfico. A partir dessas informações, a questão pede pra gente calcular o calor específico a pressão constante das duas substâncias. Os dados e as incógnitas do problema estão ilustrados pela figura abaixo. Será explicado o significado de cada dado mostrado na figura!
Para conseguir calcular o calor específico a pressão constante das duas substâncias, precisamos lembrar da única fórmula que temos pra isso. Ela é a derivada parcial da energia interna específica em relação à temperatura , mantendo o pressão da substância constante. Ou seja, é taxa de variação da entalpia específica em relação à temperatura.
Isso quer dizer que para calcular precisamos de informações sobre a variação de , mantendo a pressão constante. Para conseguir esses dados, temos que usar a primeira lei. Com ela encontraremos informações sobre a variação da energia interna específica a pressão constante. Isso é obtido, aplicando a primeira lei nessas duas substâncias ( e ).
O significado de cada variável da primeira lei será explicado no próximo passo.
Passo 2
e são as massas das substância e respectivamente. O enunciado informa todos os valores de massa. Todos eles estão presentes na figura acima!
e são as variações de energia interna específica das substância e respectivamente. Elas são importantes de serem calculadas, porque vão ajudar no cálculo dos ’s. Elas são as variações que as substâncias sofrem ao ir do ponto ao ponto .
e são os calores trocados pelos tanques e com o ambiente. Todos os dois valem zero, porque o enunciado informa que o processo de expansão é adiabático.
Com esses dados, podemos calcular as variações de energia interna específica , reorganizando a primeira lei.
Mas a entalpia específica pode ser calulada a partir da energia interna .
onde é a pressão da substância e é o volume que a substância ocupa.
Podemos usar essa fórmula para calcular a variação de entalpia específica das duas substâncias!
As pressões e são as pressões das substâncias no ponto e as pressões e são as pressões das substâncias no ponto . As pressões do ponto são iguais às pressões do ponto , porque o processo de compressão é isobárico. Elas são mostradas na figura.
Os volumes e são as pressões das substâncias no ponto e os volumes e são as pressões das substâncias no ponto . e serão calculados no próximo passo.
Passo 3
Os trabalhos de expansão e são trabalhos de movimento de fronteira à pressão constante. Como conhecemos a fórmula de trabalho de movimento de fronteira isobárico, podemos calcular e a partir dela.
Substituindo e nas equações de variação de entalpia específica, encontramos:
Vemos que as variações de entalpia específica dependem da quantidade de trabalho realizado . Perceber isso é muito importante, porque a quantidade de trabalho varia linearmente. Como a variação de depende de , também varia linearmente. Por isso, o calor específico pode ser calculado da seguinte forma.
Vemos pelo gráfico que as temperaturas das substâncias no ponto são iguais a .
Já as temperaturas dos pontos estão mostradas na figura!
Com todos esses dados, podemos enfim calcular os calores específicos!
Passo 4
Enfim, encontramos o que a gente queria!
Resposta
Exercício Resolvido #8
Elaboração própria
Considere que uma fábrica possui três tanques rígidos. Cada um dos três tanques rígidos contém uma única substância. O tanque contém da substância , o tanque contém da substância e o tanque contém da substância . Os três tanques sofrem processos adiabáticos de trabalho de eixo. O gráfico mostra a quantidade de energia fornecida por trabalho para as três substâncias em função da temperatura. Suponha que a curva de seja uma função da temperatura com a forma . Determine para qual faixa de temperatura o calor específico a volume constante da substância é maior que o calor específico a volume constante das substâncias e .
Passo 1
O enunciado fala sobre três tanques rígidos, cada um com uma substância. Eles recebem trabalho e a quantidade de trabalho que as substâncias recebem está mostrada no gráfico. A partir dessas informações a questão pede pra gente calcular o calor específico a volume constante das três substâncias para saber em que faixa de temperatura o de é maior que os ’s de e . Os dados e as incógnitas do problema estão na figura abaixo. O significado de todos os dados presentes na figura serão explicados.
Para conseguir calcular o calor específico a volume constante das três substâncias, precisamos lembrar da única fórmula que temos pra isso. Ela é a derivada parcial da energia interna específica em relação à temperatura , mantendo o volume específico da substância constante. Ou seja, é a taxa de variação de em relação à temperatura .
, e são os calores específicos das substância , e respectivamente. Para calcular os ’s, temos que conseguir informações sobre a variação da energia interna específica a volume constante a partir das informações dadas de trabalho recebido . Para fazer isso, utilizamos a primeira lei nessas três substâncias (, e ).
O significado de cada variável da primeira lei será explicado no próximo passo.
Passo 2
, e são as massas das substância , e respectivamente. O enunciado informa todos os valores de massa. Todos eles estão presentes na figura acima!
, e são as variações de energia interna específica das substância , e respectivamente. Elas são importantes de serem calculadas, porque vão ajudar no cálculo dos ’s.
, e são os calores trocados pelos tanques , e com o ambiente. Todos os três valem zero, porque o enunciado informa que o recebimento de trabalho é adiabático.
Com esses dados, podemos calcular as variações de energia interna específica , reorganizando a primeira lei.
Vemos que as variações de energia interna específica dependem da quantidade de trabalho absorvido . Perceber isso é muito importante, porque a quantidade de trabalho absorvido varia linearmente para e . Se a variação de depende de uma quantidade linear , também varia linearmente para e . Por isso, o calor específico de e pode ser calculado da seguinte forma.
Para a substância o processo é diferente. Para calcular , temos que substituir a fórmula de dada pelo enunciado na fórmula de . Essa fórmula também está presente na figura. Depois, substituímos o encontrado na derivada parcial de em relação a .
Vemos pelo gráfico que as temperaturas das substâncias no ponto 1 (, e ) são iguais a . As temperaturas dos pontos 2 ( e ) estão presentes na figura!
Com todos esses dados, podemos enfim calcular os calores específicos!
Passo 3
Antes de calcular os calores específicos, temos que calcular a variação de energia interna específica de cada substância.
Com esses valores, podemos encontrar os ’s de e .
Como o cálculo de é diferente, deixaremos ele pra próxima etapa.
Passo 4
Para calcular , temos que achar uma equação para em função de .
onde é a energia interna específica de no ponto . é um valor constante.
Substituindo essa equação na derivada parcial, achamos:
Isso significa que varia com a temperatura. A curva desse desse calor específico em função da temperatura é uma parábola com concavidade pra cima. Podemos comparar melhor com e traçando um gráfico desses calores específicos em função da temperatura.
Pelo gráfico nós vemos que o calor específico de fica maior que o calor específico de e para temperaturas maiores que !