Entalpia Específica
Produzido por Philip Canabarro BlockerTeoria
Opaa, seja bem vindo ao Responde Aí! Bora conversar sobre Entalpia e Entalpia Específica?!
O que é Entalpia?
A Entalpia nada mais é do que, o calor envolvido em um processo à pressão constante! Ela pode ser calculada à partir da seguinte fórmula:
Onde
-Ué, mas se entalpia é só calor à pressão constante, então pra que criar uma nova palavra pra isso? Eu não posso só tratar dela como calor não? 😖
Até pode…mas na prática, no dia a dia o que a gente vai usar é a entalpia específica e a vantagem dela é que ela pode ser tabelada! Imagina só se a gente tivesse que tabelar o calor de cada processo, considerando massas diferentes e pressões diferentes! 😮
Mas calma, estamos nos adiantando…Isso vai ficar bem mais claro quando fomos entender o que é a entalpia específica! Mas por enquanto você só precisa saber que a entalpia é uma propriedade extensiva, isso significa que ela depende da massa do sistema.
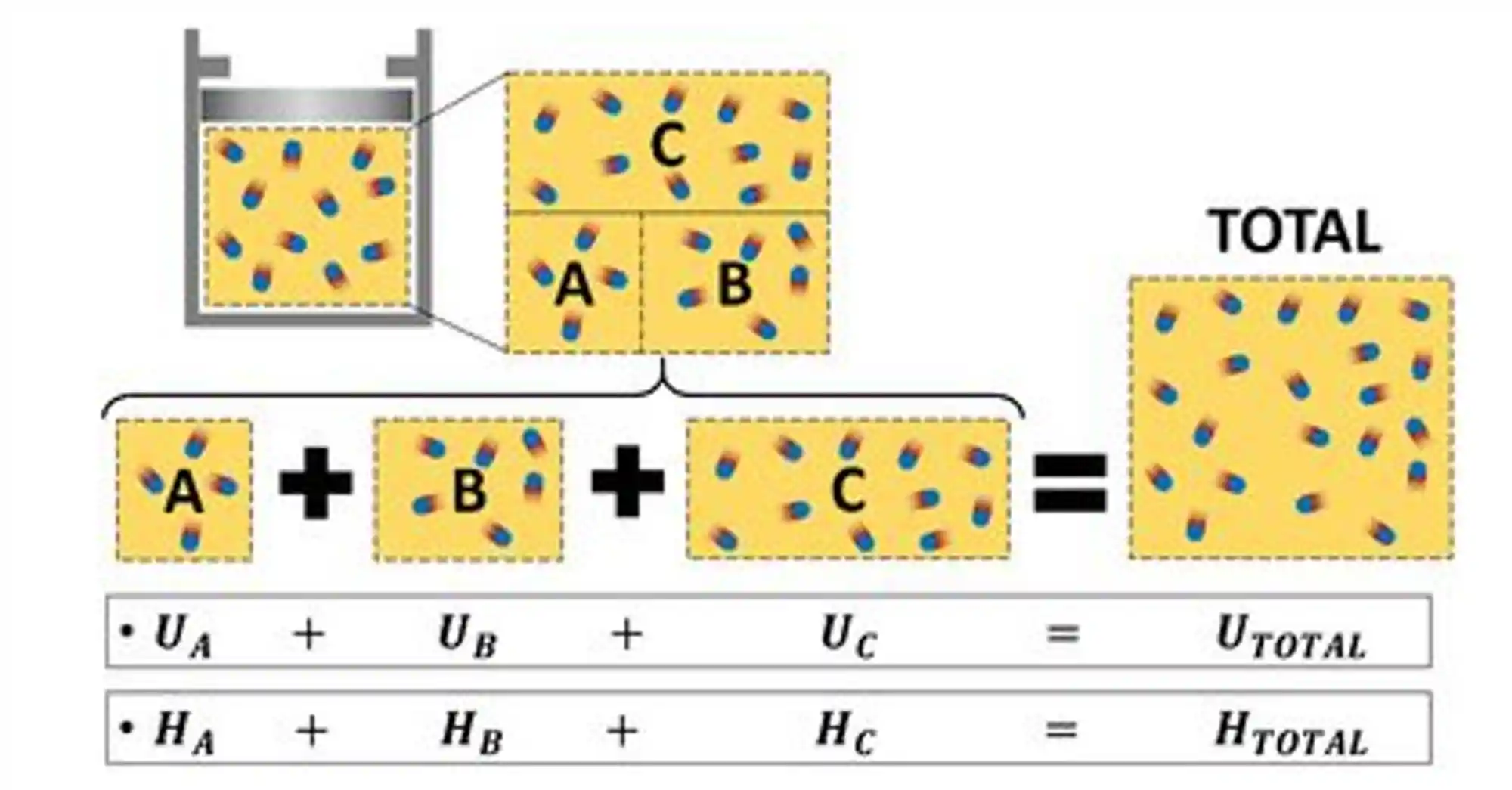
A entalpia de um sistema vai ser a soma das entalpias de cada pedacinho daquele sistema. Então quanto maior o sistema, maior a entalpia!
Entalpia Específica: Uma Propriedade Intensiva
Como falamos ali em cima a entalpia é uma propriedade extensiva, ou seja, ela depende da massa do sistema.
-Mas se a gente dividir a entalpia pela sua massa?! Como que fica?
É ai que nasce a entalpia específica, que é exatamente isso que a gente terminou de falar! A entalpia dividida pela massa da amostra e agora ela é uma propriedade intensiva, já que ela não depende mais da massa do sistema!
É importante perceber que a unidade de entalpia específica é
Para o nosso exemplo a entalpia específica é igual a
📢 Clique para saber mais:
Entalpia Específica de uma Mistura Bifásica
Vamos imaginar que, dentro de um recipiente temos uma mistura bifásica saturada! Isso é, uma substância que está em duas fases diferentes e essas fases estão equilíbrio termodinâmico, como por exemplo a água na forma de líquido saturado e vapor saturado!
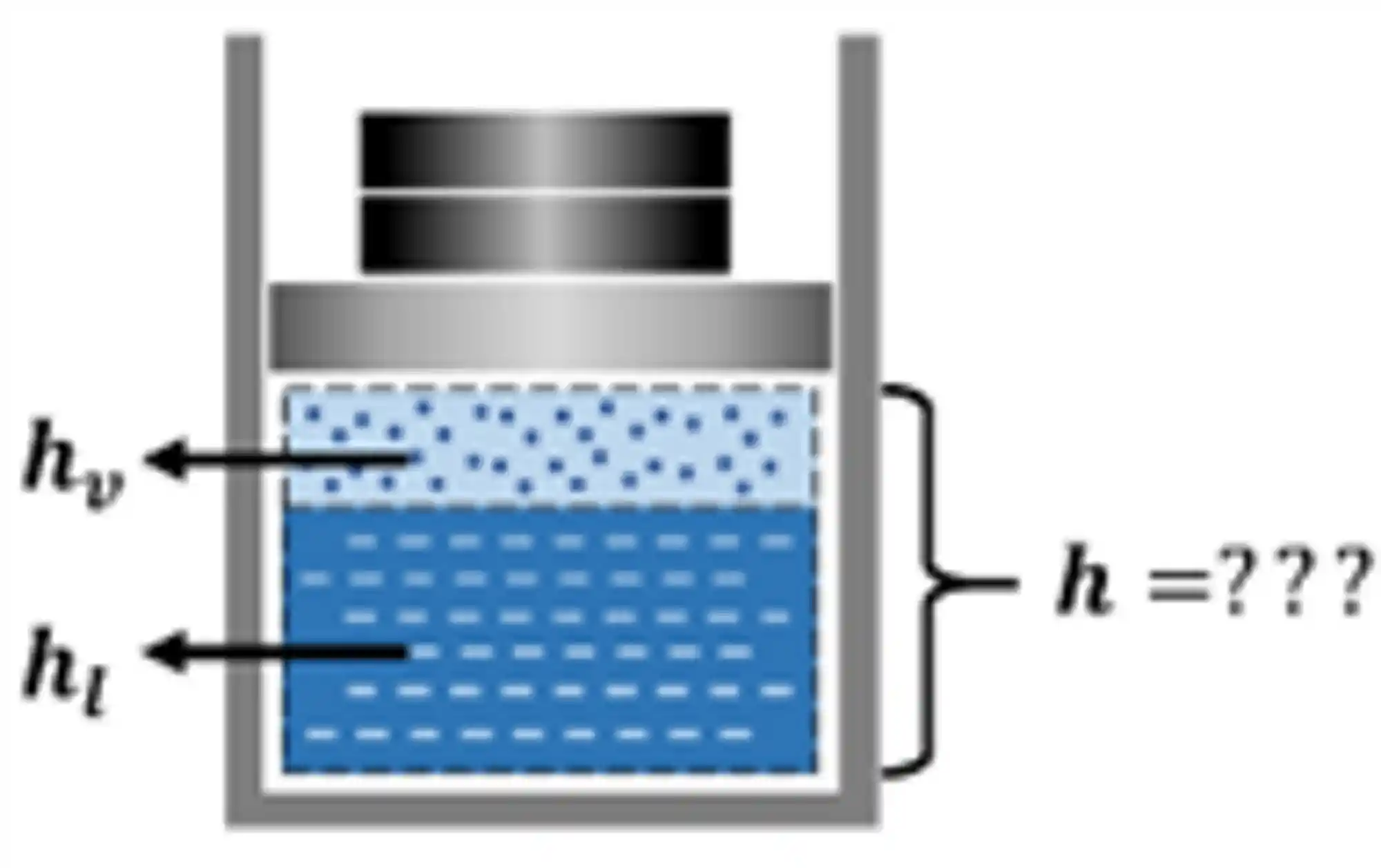
Como podemos calcular a entalpia específica dessa mistura bifásica?!
Fazer esse cálculo é mais fácil do que parece! A fórmula de entalpia específica para mistura de vapor saturado com líquido saturado é dada por:
onde
Entalpia da Água Líquida Saturada e do Vapor Saturado
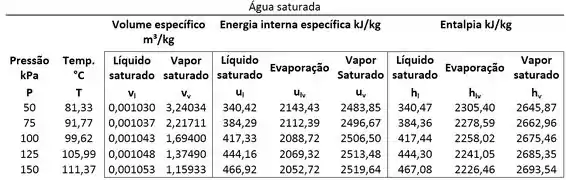
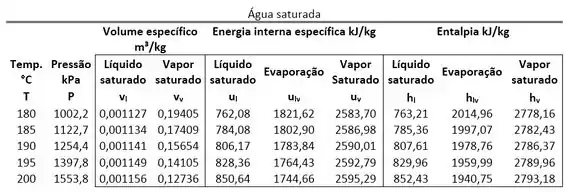
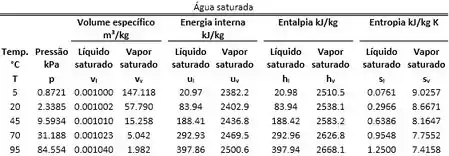
Para calcular a entalpia específica da mistura, precisamos dos valores da entalpia específica do líquido saturado e do vapor saturado. Esses dados podem ser obtidos nas tabelas de propriedades termodinâmicas, como podemos observar abaixo:
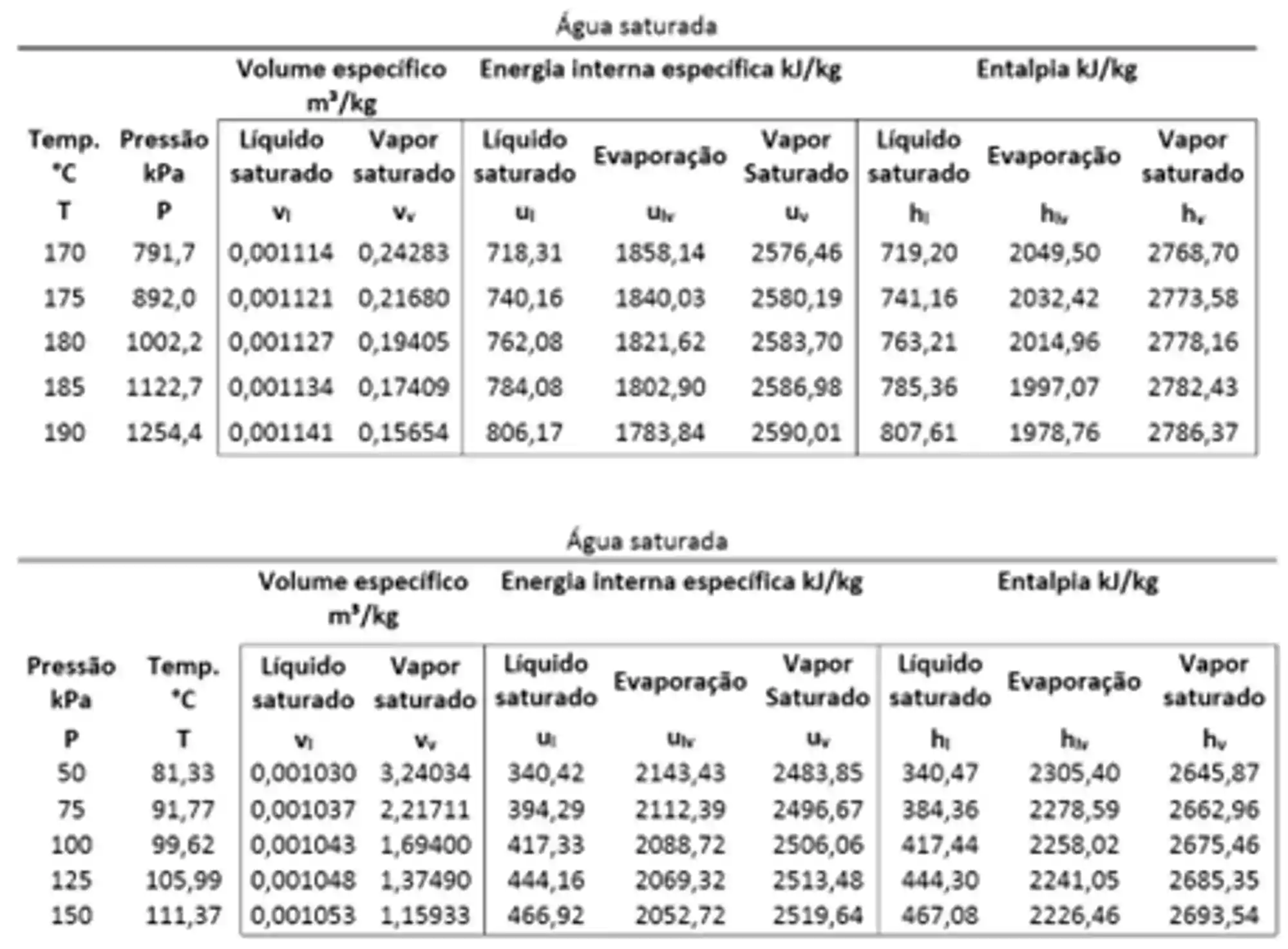
As tabelas acima mostram o valor de
Na primeira tabela temos as propriedades termodinâmicas em função da temperatura da água saturada e na tabela de baixo temos os mesmos dados, mas agora em função da pressão da água saturada!
Exemplo: Calcule a Entalpia Específica de uma mistura bifásica à 75 kPa com uma
Para fazer esse cálculo vamos usar a fórmula:
Pela tabela termodinâmica sabemos que:
Substituímos os dados na fórmula e calculamos a entalpia da mistura:
Ou seja, a entalpia específica da mistura é igual a 2093,4 kJ/kg.
Agora vamos praticar com exercícios?
Entalpia Específica de uma Mistura Bifásica
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Determine a entalpia de um balde com de água líquida saturada à pressão atmosférica de . Use a tabela abaixo.
Passo 1
Devemos primeiro visualizar o exercício através da figura do balde de água líquida.
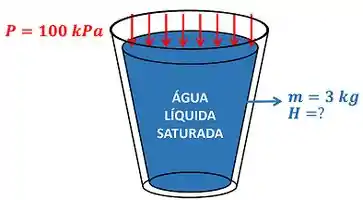
O enunciado pede para a gente encontrar a entalpia de de água líquida saturada, mas a tabela que ele nos deu tem apenas valores de entalpia específica . Como podemos resolver esse problema? Lembrando da fórmula da entalpia em função da entalpia específica.
Essa fórmula mostra pra gente que para encontrar só precisamos multiplicar pela massa do sistema! Então quanto valem e ? Começando pelo , vemos que o valor de para líquido saturado está na mesma linha que a pressão de e na mesma coluna que .
A massa é informada pelo próprio enunciado:
Vamos encontrar na próxima etapa e depois vamos usar a fórmula para achar .
Passo 2
Como podemos extrair o da tabela? Lembrando que ele fica na mesma linha que a pressão da água e na mesma coluna que .
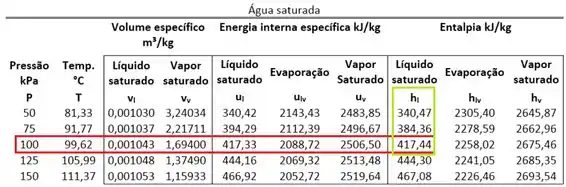
Então:
Sabendo disso, já podemos usar a fórmula de entalpia no próximo passo!
Passo 3
Esse é o resultado que queríamos!
Resposta
Exercício Resolvido #2
Elaboração própria
Determine a energia interna de um tanque rígido fechado que contém de vapor d’água saturado à pressão de . Use a tabela abaixo.
Passo 1
Devemos primeiro visualizar o exercício através da figura do tanque rígido com vapor saturado de água.
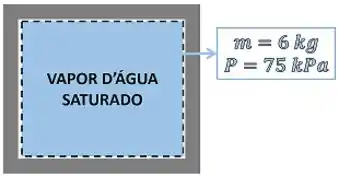
O enunciado pede para a gente encontrar a energia interna de de vapor d’água saturado, mas a tabela que ele nos deu tem apenas valores de entalpia específica . Como podemos resolver esse problema?

A solução dessa questão precisa ser dividida em duas etapas. Primeiro, temos que converter a entalpia específica da tabela para energia interna específica . Fazemos isso, reorganizando a fórmula da entalpia específica.
Usando essa fórmula, podemos converter a entalpia específica do vapor saturado para energia interna específica do vapor saturado .
e são obtidos pela tabela de saturação da água. Eles estão na mesma linha que a pressão de da água.
Segundo, para converter a energia interna específica do vapor saturado para a energia interna do vapor saturado , usamos a fórmula abaixo.
Essa fórmula mostra pra gente que para encontrar só precisamos multiplicar pela massa do sistema! Então quanto vale a massa de vapor d’água ?
A massa é informada pelo próprio enunciado:
Vamos encontrar na próxima etapa e depois vamos usar a fórmula para achar .
Passo 2
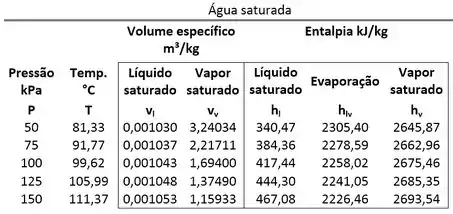
Como podemos extrair o da tabela?
Lembrando que ele fica na mesma linha que a pressão da água e na mesma coluna que !
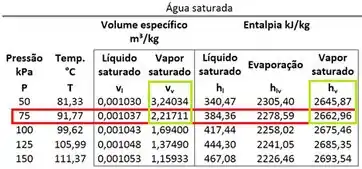
Então:
O volume específico do vapor também é obtido nessa tabela.
Sabendo disso, já podemos usar a fórmula de conversão de entalpia para energia interna no próximo passo!
Passo 3
Agora podemos concluir o último passo de calcular a energia interna do vapor
Esse é o resultado que queríamos!
Resposta
Exercício Resolvido #3
Elaboração própria
Um tanque rígido possui uma mistura de água líquida saturada com de vapor d’água saturado com um título de 0,3. Considerando que ambos estão a de pressão, determine a entalpia da mistura. Use a tabela abaixo.
Passo 1
Devemos primeiro visualizar o exercício através da figura do tanque rígido com a mistura dentro.

O enunciado pede para a gente encontrar a entalpia da mistura de água líquida saturada com vapor saturado d’água, mas a tabela que ele nos deu tem apenas valores de entalpia específica . Como podemos resolver essa questão? Lembrando da fórmula da entalpia de líquido e vapor saturados em função das entalpias específicas.
Essa fórmula mostra pra gente que para encontrar só precisamos multiplicar pela massa do sistema! Então quanto valem e ? Os valores de e são extraídos das tabelas.
A massa de vapor é informada diretamente pelo enuciado.
Já a massa de líquido só pode ser calculada indiretamente:
A massa total da mistura pode ser descoberta pela fórmula do título.
Vamos encontrar e na próxima etapa e depois vamos usar as fórmulas para achar .
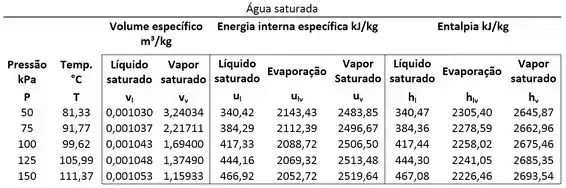
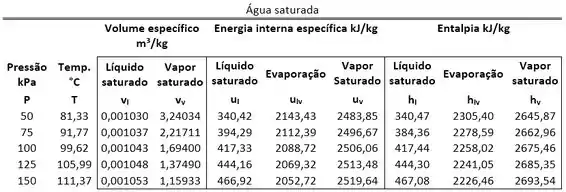
Passo 2
Como podemos extrair e da tabela? Lembrando que eles ficam na mesma linha que a pressão da água e na mesma coluna que .
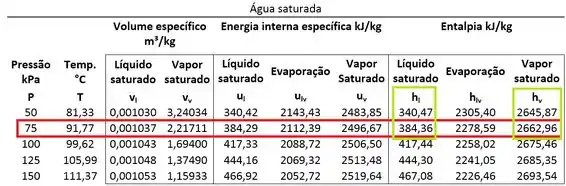
Então:
Sabendo disso, já podemos usar as fórmulas de entalpia no próximo passo!
Passo 3
Para o vapor saturado a equação é:
Para calcular a entalpia do líquido, precisamos primeiro calcular a massa de líquido e a massa total.
Agora sim usamos a fórmula de entalpia para o líquido.
A entalpia total é a soma das duas partes da mistura. Vapor e líquido.
Resposta
Exercício Resolvido #4
Elaboração própria
Determine se a água é um vapor superaquecido, um líquido comprimido ou se ela está saturada, usando a tabela de propriedades dada. Considere o seguinte caso:
, e .
Passo 1
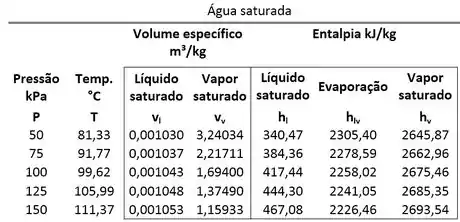
Para saber se a água está em uma dessas três opções. Devemos comparar sua energia interna específica com as energias internas específicas do vapor saturado e do líquido saturado . Mas como podemos fazer essa comparação se o enunciado só mostra valores de entalpia específica na tabela? Convertendo os valores de entalpia para energia interna!

E como fazemos essa conversão? Reorganizando a fórmula de entalpia!
Usando essa fórmula, podemos converter para e para .
O enunciado informa que:
Para achar , , e temos que usar a tabela de saturação. Os valores estão na mesma linha da pressão de .
Porém ele não informa diretamente. Para calculá-lo, precisamos lembrar que:
Temos todos esses valores. Agora é só aprender a descobrir a fase da água! Faremos isso na próxima etapa.
Passo 2
Agora vamos comparar esses valores com as condições de saturação da água informadas pela tabela!
Se a energia interna específica for maior que a energia interna específica do vapor saturado a de pressão , então a água é um vapor superaquecido.
Se for menor que a energia interna específica do líquido saturado a de pressão , a água é um líquido comprimido.
Por fim, se o valor de estiver entre e , a água está saturada.
Sabendo disso vamos achar as três energias internas (, e ) e fazer a comparação!
Passo 3
Vemos que para as energias internas do líquido saturado e vapor saturado são:
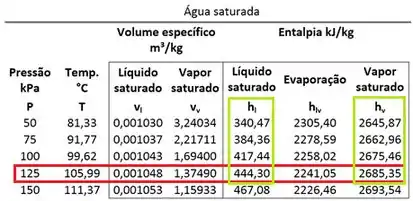
Podemos calcular achar a energia interna específica da água pela fórmula.
Comparando essa energia interna específica com as energias internas de saturação, vemos que:
Logo a água é um vapor superaquecido!
Resposta
A água é um vapor superaquecido.
Exercício Resolvido #5
Elaboração própria
Determine a entalpia específica da água, usando as tabelas de propriedades dada. Considere o seguinte caso:
, e .
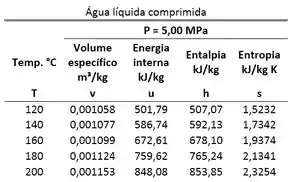
Passo 1
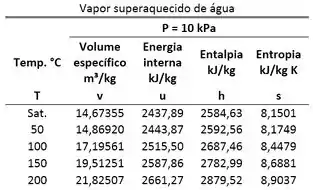
Primeiro, para saber qual tabela devemos usar, devemos comparar o volume específico da água com os volumes específicos do vapor saturado e do líquido saturado para temperatura igual a que estão na tabela de saturação.
O enunciado informa que:
Porém ele não informa diretamente. Para calculá-lo, precisamos lembrar que:
Temos todos esses valores. Agora é só aprender a descobrir a fase da água para determinar qual tabela vamos usar! Faremos isso na próxima etapa.
Passo 2
Agora vamos aprender a comparar o volume específico da água com os volumes específicos informados pela tabela para conhecer a fase da água.
Se volume específico for maior que volume específico do vapor saturado a , então a água é um vapor superaquecido e precisaremos usar a tabela de vapor superaquecido.
Se for menor que volume específico do líquido saturado a , a água é um líquido comprimido. Aí teremos que usar a tabela de líquido comprimido.
Por fim, se o valor de estiver entre e , a água está saturada.
Antes de comparar esses valores, precisamos entender a pegadinha dessa questão e alguns outros tópicos. É sobre isso que o próximo passo vai falar!
Passo 3
Atenção para a seguinte pegadinha! Ainda não sabemos se podemos usar as tabelas de vapor superaquecido e de líquido comprido, porque elas só podem ser usadas paras as pressões de e respectivamente e ainda não sabemos a pressão da água!

Além dessa pegadinha, devemos nos preocupar em achar o título da água, caso ela esteja saturada! Como podemos fazer isso? Reorganizando a fórmula de volume específico médio para mistura!
Só com esse valor que seremos capazes de calcular a entalpia específica da água caso ela seja uma mistura entre vapor e líquido. Quando ela for uma mistura saturada, a fórmula de entalpia específica vai precisar dessa variável.
Agora vamos encontrar os três volumes específicos (, e ) e descobrir qual é a fase da água!
Passo 4
Vemos que para os volumes do líquido saturado e vapor saturado são:
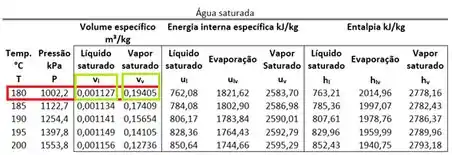
Podemos calcular achar o volume específico da água pela fórmula.
Comparando esse volume específico com volumes específicos de saturação, vemos que:
Logo a água está saturada! Ou seja, precisaremos usar apenas a tabela de saturação para descobrir a sua entalpia específica. Como seu volume específico está entre os dois valores de saturação, sabemos também que ela é uma mistura saturada com o título valendo:
Ou seja, para calcularmos a sua entalpia específica temos que encontrar o valor do título. E é exatamente isso que faremos na próxima etapa!
Passo 5
Agora só falta obter os valores de entalpia específica através da tabela para encontrarmos o resultado que queremos. Conseguimos cumprir esse passo, olhando para a tabela a seguir:
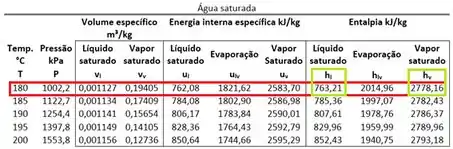
Substituindo esses valores na equação principal, alcançamos o resultado final:
Resposta
Exercício Resolvido #6
Elaboração própria
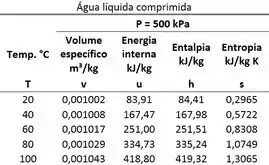
Inicialmente, a água de uma amostra se encontra como líquido saturado a . A água é então comprimida, em um processo isotérmico, até que a pressão atinja . Determine a entalpia específica do estado final. Use as tabelas termodinâmicas abaixo.
Passo 1
Esse exercício pede que a gente descubra o valor da entalpia específica da água, depois dela passar por um processo isotérmico. Ou seja, a água tinha um estado inicial (estado 1) e, depois de passar por esse processo, alcança seu estado final (estado 2). A figura abaixo mostra todas as informações dadas pelo enunciado.
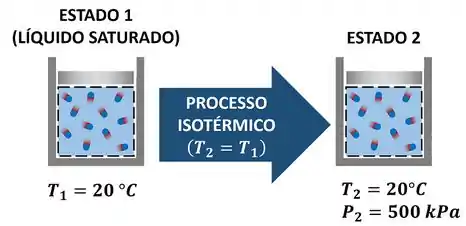
Como podemos achar a entalpia específica do estado 2 ? Nós precisamos conhecer duas propriedades intensivas do estado 2 para poder determinar o valor de todas as propriedades nesse estado. Uma nós já temos: a pressão informada pelo enunciado.
Nós podemos encontrar a outra propriedade, lembrando que o processo pelo qual a água passa é isotérmico. Isso significa que a temperatura do estado 2 é igual à temperatura do estado 1.
A temperatura do estado 1 é fornecida pelo enunciado:
Pronto! Temos duas propriedades do estado 2. Com essa informação, nós podemos encontrar a entalpia específica da água, usando as tabelas de propriedades termodinâmicas. Mas qual delas devemos usar para achar ?
É isso que descobriremos no próximo passo!
Passo 2
Se o estado 2 for líquido comprimido, usamos a tabela de líquido comprimido. Se o estado 2 for saturado, usamos a tabela de saturação para encontrar ! Para saber isso, comparamos a pressão de saturação para a água a com sua temperatura .

Caso a água tenha pressão maior que a pressão de saturação, ela é um líquido comprimido!
Caso ela tenha pressão igual à pressão de saturação, ela estará saturada.
Pronto, agora que temos todas as informações que precisamos, vamos iniciar nossos cálculos.
Passo 3
Começamos as contas, descobrindo a pressão de saturação da água a . Para conseguir esse valor, usamos a tabela de saturação.
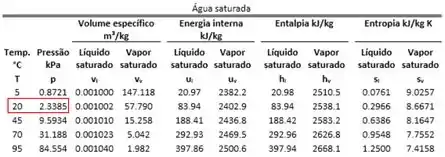
Isso significa que a pressão do estado 2 é maior que a pressão de saturação. Por isso, a água no estado 2 é um líquido comprimido. Ou seja, para achar precisamos usar a tabela de líquido comprimido. Isso é o que faremos no próximo passo.
Passo 4
A entalpia do estado 2 tem que estar na mesma linha que a temperatura de .
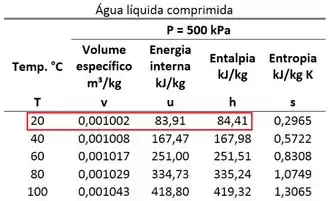
Logo, vale:
Resposta
Exercício Resolvido #7
Elaboração própria
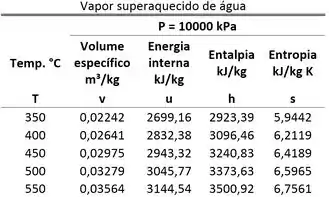
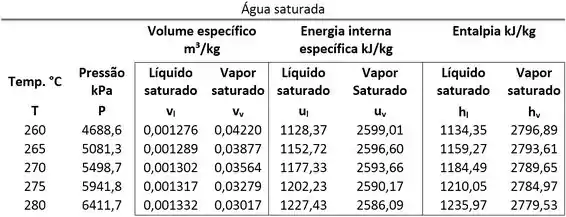
Vapor d’água é resfriado em um processo a volume específico constante de e até uma temperatura de . Determine a entalpia específica final da água. Use as tabelas de propriedades abaixo.
Passo 1
Esse exercício pede que a gente descubra o valor da entalpia específica da água, depois dela passar por um processo de resfriamento que mantém o seu volume específico igual. Ou seja, a água tinha um estado inicial (estado 1) e, depois de passar por esse processo, alcança seu estado final (estado 2). A figura abaixo mostra todas as informações dadas pelo enunciado.
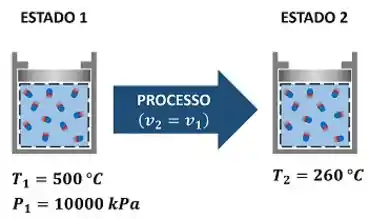
Como podemos achar a entalpia específica do estado 2 se nós só conhecemos o estado 1? Precisamos conhecer mais uma propriedade intensiva do estado 2 para fixarmos este estado e descobrirmos as suas propriedades intensivas restantes. Mas como faremos isso? Por enquanto só conhecemos a temperatura desse estado final .

Fazemos isso encontrando o valor de volume específico do estado 1 ! Como o processo mantém o volume específico da água igual, temos que:
Ou seja, dessa forma descobrimos mais uma propriedade intensiva do estado 2 e conseguimos fixar esse estado. A partir daí, achamos a entalpia específica através da tabela de propriedades!
Mas como encontramos o volume específico ?

Nós achamos o valor de através da tabela de vapor superaquecido!
Passo 2
Já sabemos a fase do estado 1! Como podemos descobrir a fase do estado 2, comparando o seu volume específico com os volumes específicos de saturação ( e )?

Se volume específico for maior que volume específico do vapor saturado a , então a água é um vapor superaquecido e precisaremos usar a tabela de vapor superaquecido.
Se o valor de estiver entre e , a água está saturada.
Se o estado 2 for vapor superaquecido, achamos a entalpia específica, olhando a tabela de vapor superaquecido. E se o estado 2 for um estado saturado, como encontramos sua entalpia específica ? Usamos o ou o da tabela de saturação? Caso o estado 2 seja saturado, a entalpia específica tem a seguinte fórmula:
onde é o título do estado saturado 2.
Mas como podemos encontrar o valor de ? Se liga na dica: se queremos encontrar o título da mistura saturada e já sabemos o seu volume específico, podemos usar a fórmula a seguir:
onde é o volume específico do vapor saturado na temperatura do estado 2 e é o volume específico do líquido saturado na temperatura do estado 2 .
Pronto, agora que temos todas as informações que precisamos, vamos iniciar nossos cálculos.
Passo 3
Como o estado 1 é vapor superaquecido, encontramos o volume específico desse estado olhando para a tabela de vapor superaquecido.
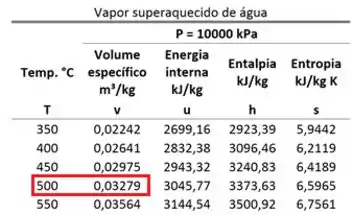
Como o volume específico do estado 2 é igual ao volume específico do estado 1, descobrimos que:
Ou seja, a temperatura do estado 2 vale e o volume específico do estado 2 vale . Já fixamos este estado. Agora só falta saber qual é a fase do estado 2 para encontrarmos a sua entalpia específica .
Passo 4
Vemos pela tabela de saturação que os volumes específicos saturados valem:
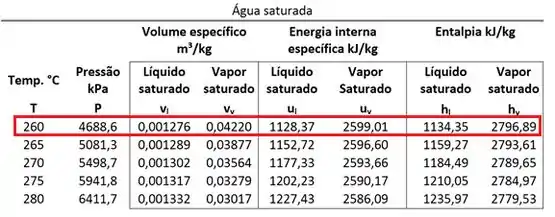
O volume específico do estado 2 está entre esses dois valores. Logo, o estado 2 é saturado.
Então, para calcular temos que conhecer o título da mistura saturada.
Nessa tabela, também encontramos também os valores das entalpias de saturação que serão importantes para o cálculo de .
Substituindo esse valor na fórmula de :
Resposta
Exercício Resolvido #8
Elaboração própria
Um tanque fechado e rígido contém uma mistura líquido-vapor de Refrigerante 22 inicialmente a com um título . Energia é transferida para o tanque sob forma de calor até que o sistema esteja sob . Determine a entalpia específica final, sabendo que após o aquecimento o Refrigerante 22 é um vapor superaquecido. Use as tabelas de propriedades abaixo.
Passo 1
Esse exercício pede que a gente descubra o valor da entalpia específica do Refrigerante 22, depois dele passar por um processo de aquecimento. Ou seja, o Refrigerante 22 tinha um estado inicial (estado 1) e, depois de passar por esse aquecimento, alcança seu estado final (estado 2). A figura abaixo mostra todas as informações dadas pelo enunciado.
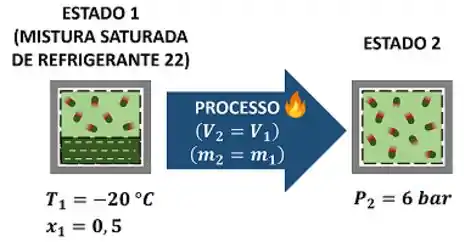
Como podemos achar a entalpia específica do estado 2 se nós só conhecemos o estado 1? Precisamos conhecer mais uma propriedade intensiva do estado 2 para fixarmos este estado e descobrirmos as suas propriedades intensivas restantes. Mas como faremos isso? Por enquanto, só conhecemos a pressão desse estado .

Fazemos isso levando em conta algumas informações que estão escondidas no enunciado. A primeira delas é obtida, quando o enunciado fala que o Refrigerante 22 está contido em um tanque rígido. Se o tanque é rígido, ele permanece com o mesmo volume durante o aquecimento. Ou seja, se o tanque é rígido, o volume que o Refrigerante 22 ocupa não muda.
A outra informação escondida é obtida na parte em que o enunciado diz que o tanque rígido está fechado. Isso significa que não tem massa de Refrigerante 22 entrando ou saindo do tanque. Logo, a massa de Refrigerante 22 não muda.
Como o volume e a massa do Refrigerante 22 permanecem iguais durante todo o processo, seu volume específico também permanece igual:
Ou seja, dessa forma descobrimos mais uma propriedade intensiva do estado 2 e conseguimos fixar esse estado. A partir daí, achamos a entalpia específica através da tabela de propriedades!
Mas como encontramos o volume específico ?

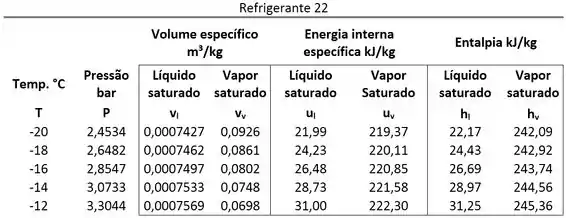
Através da tabela de saturação! Como o estado 1 é uma mistura saturada de líquido e vapor de Refrigerante 22, o volume específico é dado pela fórmula abaixo.
onde:
- é o título da mistura saturada. Ele vale 0,5 segundo o enunciado;
- é o volume específico do líquido saturado contido na mistura. Ele está a segundo o enunciado;
- é o volume específico do vapor saturado contido na mistura. Ele está a segundo o enunciado.
Vamos descobrir no próximo passo como calcular pela tabela de saturação.
Passo 2
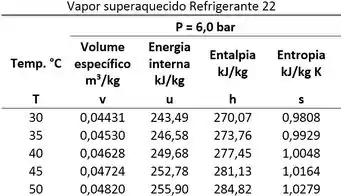
Como o estado 2 é um vapor superaquecido, usaremos a tabela de vapor superaquecido para encontrar .

Na tabela, precisamos encontrar a entalpia específica do Refrigerante 22 a de pressão e com volume específico . Caso o volume específico não seja igual a nenhum volume específico da tabela, teremos que interpolar pela equação abaixo.
onde:
- é o volume específico presente na tabela que é menor que ;
- é o volume específico presente na tabela que é maior que ;
- é a entalpia específica presente na tabela que é menor que ;
- é a entalpia específica presente na tabela que é maior que .
Pronto, agora que temos todas as informações que precisamos, vamos iniciar nossos cálculos.
Passo 3
Começamos as contas, calculando o valor de pela tabela de saturação e pela sua fórmula.
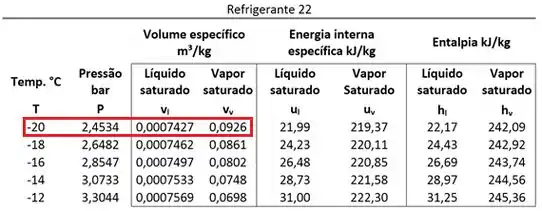
Como o volume específico do estado 2 é igual ao volume específico do estado 1:
Como esse valor de volume específico não aparece na tabela de Refrigerante 22 vapor superaquecido a de pressão, precisaremos interpolar . Vamos deixar isso pro passo seguinte.
Passo 4
Pela tabela, descobrimos que está entre dois valores de volume específicos:
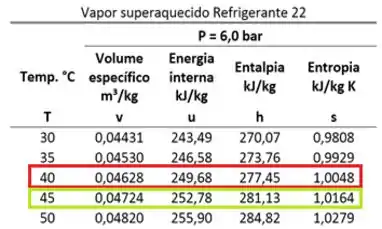
A entalpia específica do Refrigerante 22 , quando ele tem um volume específico igual a , vale:
A entalpia específica do Refrigerante 22 , quando ele tem um volume específico igual a , vale:
Substituindo esses valores na equação de interpolação encontramos:
Esse é o resultado final que o enunciado pede!