Regime Transiente
Produzido por Philip Canabarro BlockerTeoria
Opa! Seja bem vindo ao Responde Aí! Bora aprender sobre Regime Transiente de uma vez por todas?!
Regime Permanente x Regime Transiente
No balanço de massa de processos em regime permanente e sem reação, acontece a gente corta sem dó nem piedade, os termos de geração e acúmulo. Assim:
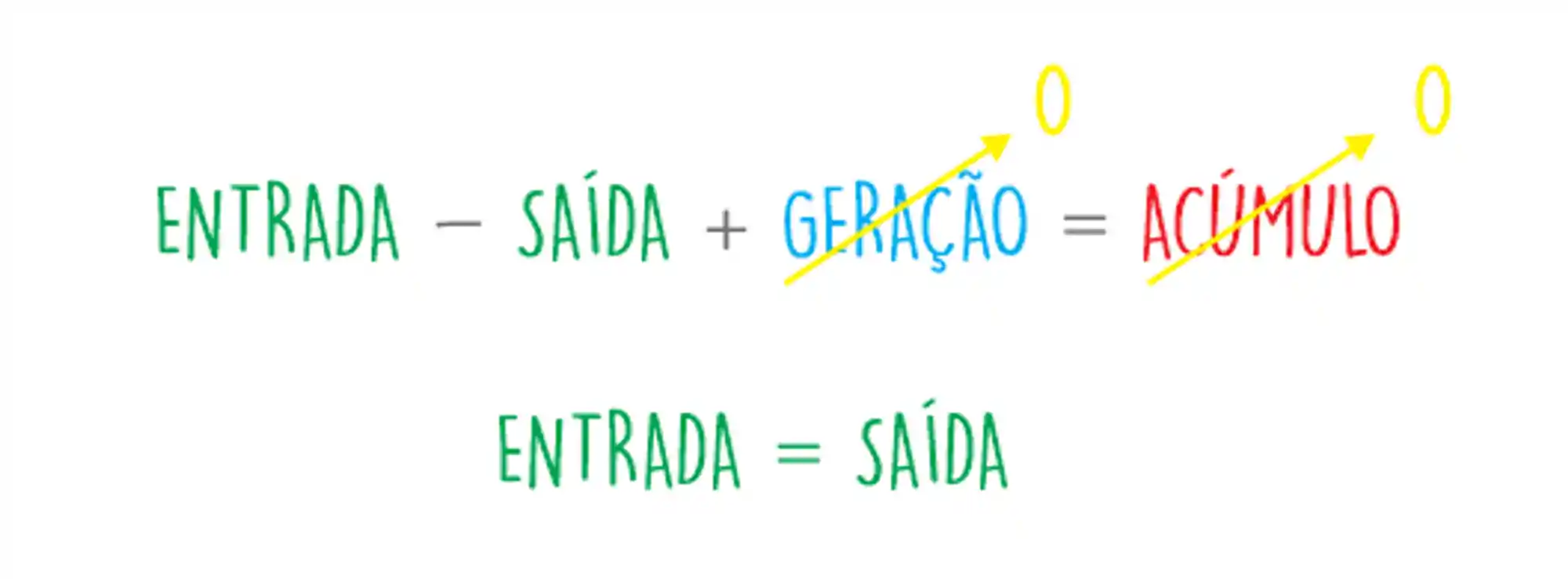
O mesmo acontece para o balanço de energia. Mas, sinto muito te informar, mas a mamata acabou! Não podemos mais ignorar o acúmulo 🥲
Mas não se preocupa, não precisa ficar preocupado com o acúmulo! Hoje a gente vai aprender a fazer os balanços de massa e de energia no regime transiente…passo a passo, pra não ficarem dúvidas!
📢 Clique para saber mais:
- Regime Transiente: Exercícios Resolvidos
- Conservação de Energia do Volume de Controle
- Conservação de Massa do Volume de Controle
Exemplo de um sistema em Regime Transiente
Vamos imaginar que queremos encher uma piscina, mas ela esta furada! Se liga no esquema abaixo:
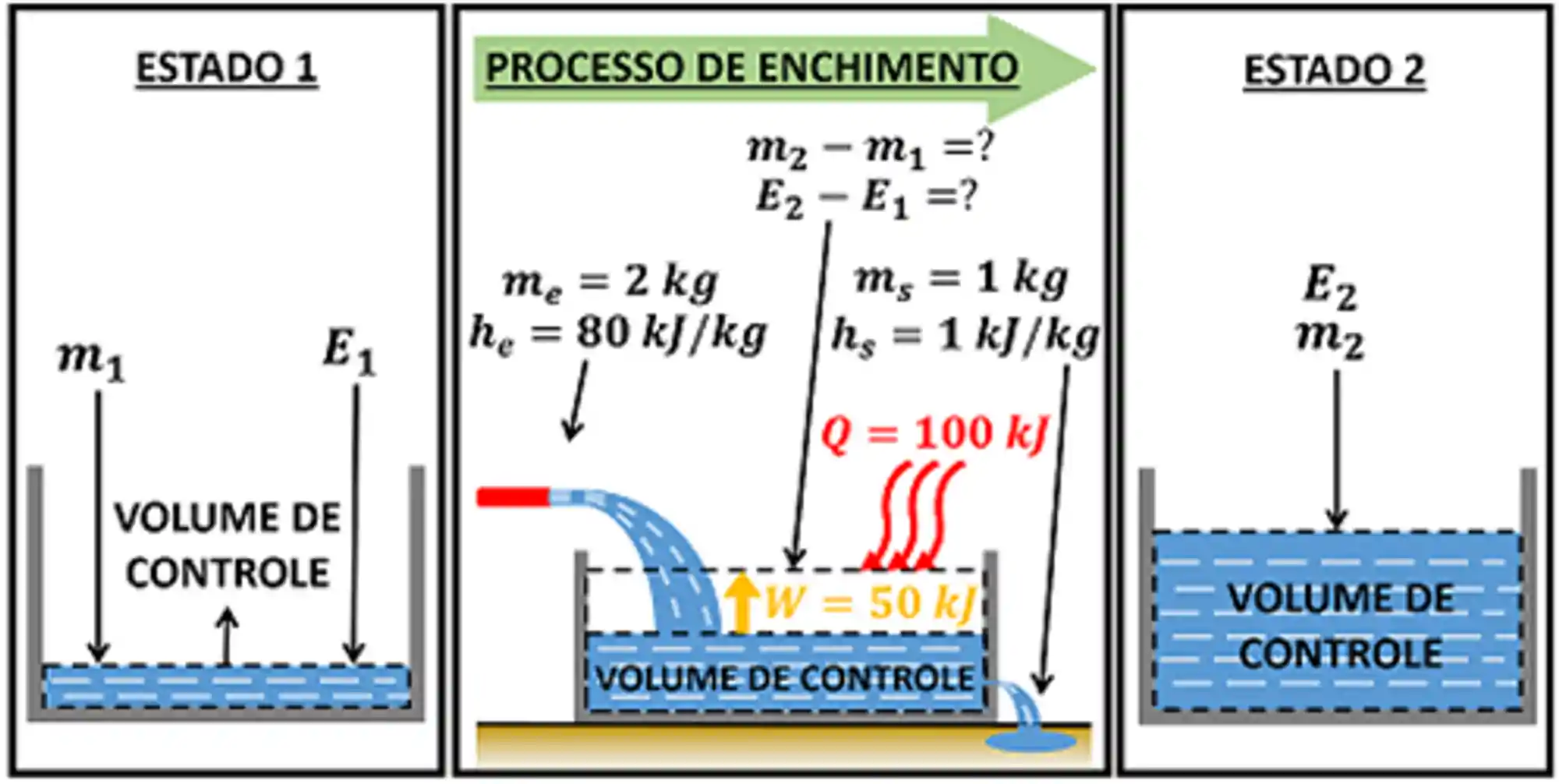
A piscina recebe
Esse é um enunciado típico de processos em regime transiente! Ele pede que a gente calcule a variação de massa e energia da piscina. Ou seja, ele quer saber o valor de duas diferenças:
- A diferença entre a massa
que a piscina passou a ter depois do processo transiente de enchimento e a massa que a piscina tinha. - A diferença entre a energia
que a piscina passou a ter depois do processo e a energia que a piscina tinha.
Em outras palavras, o problema só está interessado nos estados inicial e final da piscina. Ele não nos obriga a saber o valor da massa da piscina a cada instante nem o valor da energia da piscina a cada instante!
Confira também esse conteúdo em vídeo:
Conservação de Massa no Regime Transiente
Precisamos aprender a calcular as variações de energia e massa de um processo em regime transiente. Para fazer isso, a gente tem que se lembrar que a energia e a massa se conservam! Imagine a seguinte situação:
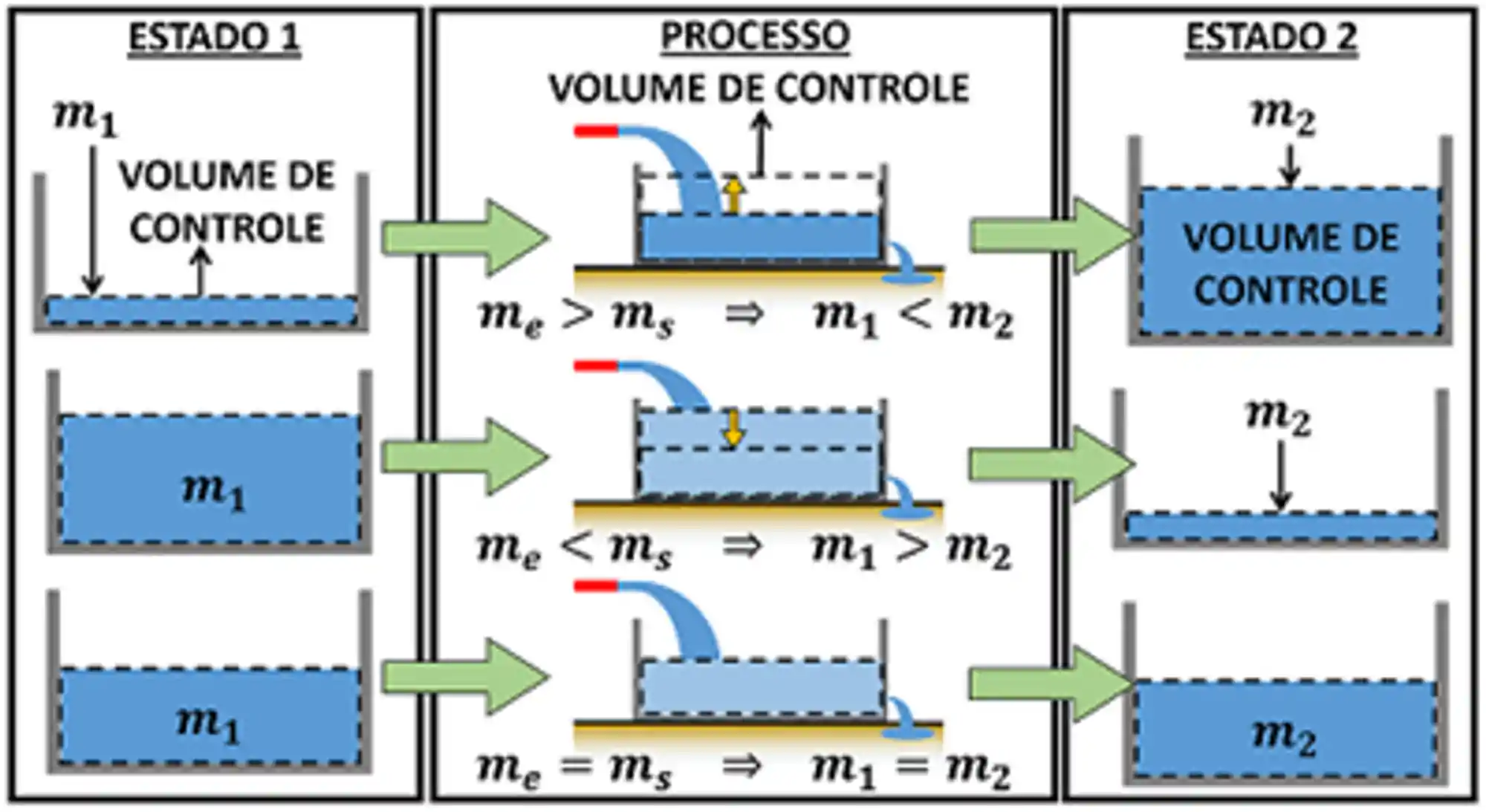
A variação da massa dentro do volume de controle
Onde:
é a massa do volume de controle depois dele passar por um processo em regime transiente; é a massa do volume de controle antes dele passar por um processo em regime transiente; é a quantidade de massa que entra no volume de controle durante o processo em regime transiente; é a quantidade de massa que sai do volume de controle durante o processo em regime transiente.
Essa fórmula é a conservação de massa para processos em regime transiente! 🤩
Variação de Energia no Regime Transiente
Quando a massa sai do volume de controle ela leva junto com ela a sua entalpia, a sua energia cinética e a sua energia potencial. Ou seja:
Onde:
é a entalpia específica da massa que sai do volume de controle. Sua unidade no Sistema Internacional (S.I.) é o joule por quilograma ; é a velocidade da massa saindo do volume de controle. Sua unidade no S.I. é o metro por segundo ; é a altitude da massa, quando ela está entrando está saindo do volume de controle. Sua unidade no S.I. é o metro (m).
Agora, quando a massa entra no volume de controle ela traz junto com ela a sua própria entalpia, a sua energia cinética e a sua energia potencial. Com isso temos:
Onde:
é a entalpia específica da massa que entra do volume de controle; é a velocidade da massa saindo do volume de controle; é a altitude da massa na entrada.
Primeira Lei da Termodinâmica no Regime Transiente
A gente também pode calcular a variação de energia nos pontos 1 e 2 diminuindo
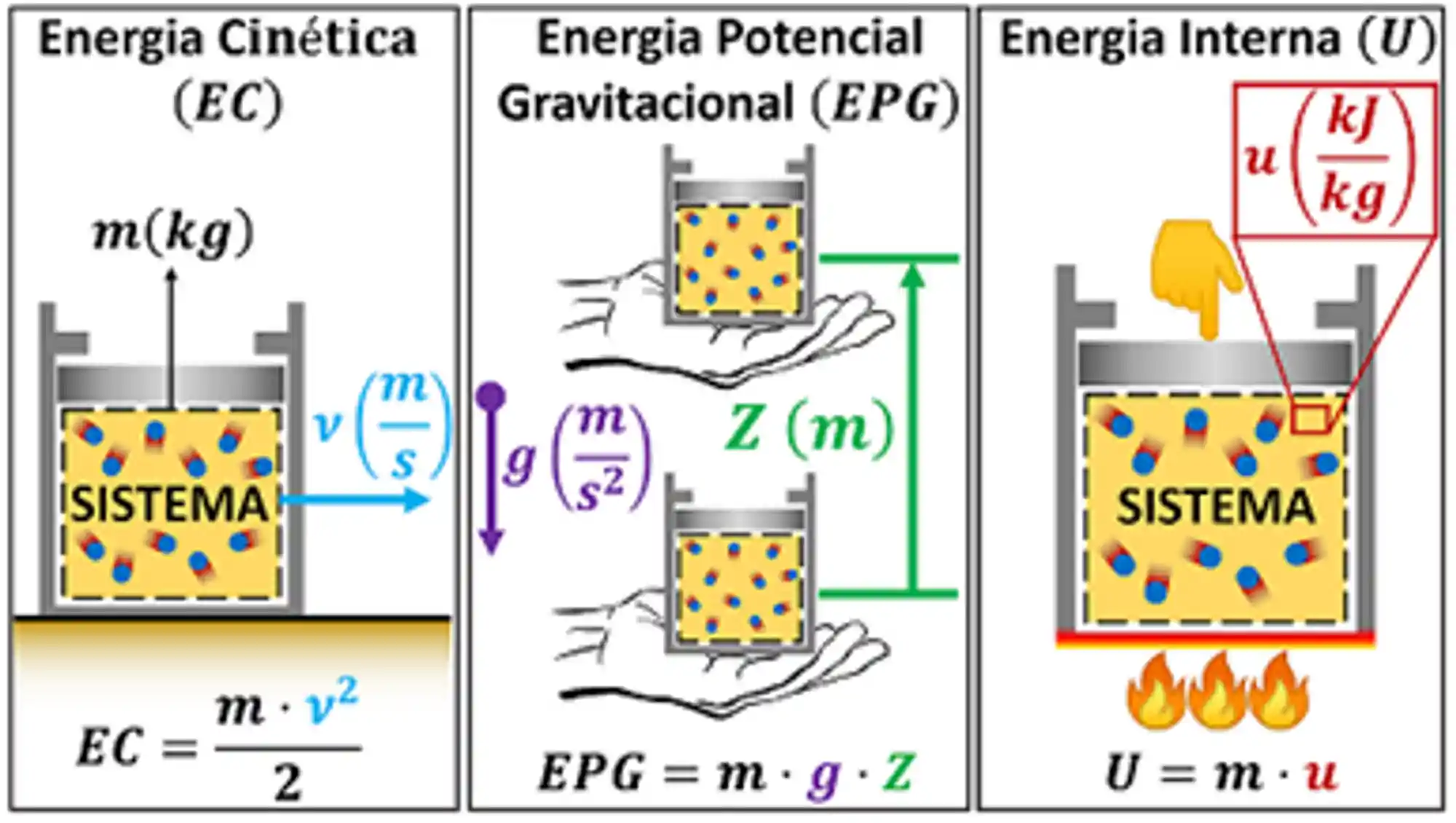
A Energia nos pontos 1 e 2 pode ser calculada por:
Substituindo essas duas fórmulas na fórmula de variação de energia, encontramos a forma completa da primeira lei para processos em regime transiente.
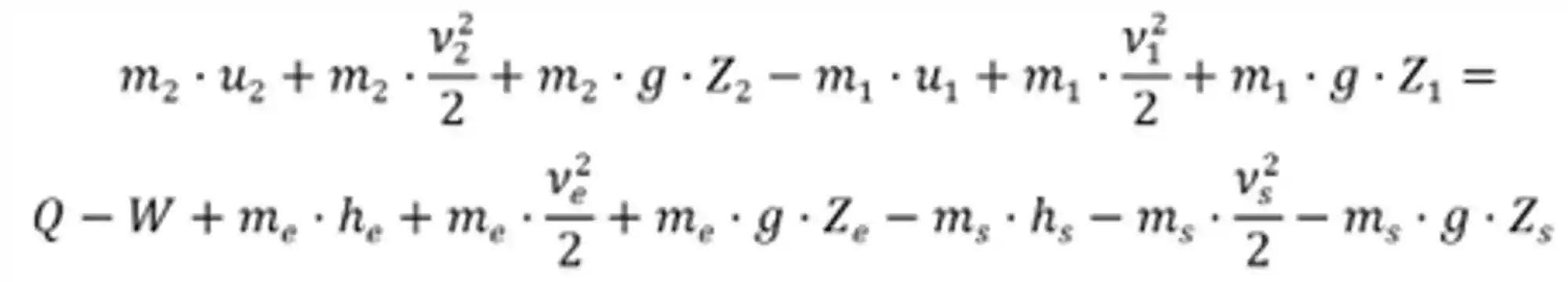
Considerando a variação de energia potencial e cinética igual a zero, a primeira lei da
Agora vamos praticar com exercícios?
Conservação de Massa no Regime Transiente
Variação de Energia no Regime Transiente
Primeira Lei da Termodinâmica no Regime Transiente
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Um conjunto cilindro-pistão termicamente isolado está inicialmente evacuado e começa a ser preenchido com ar a . Quando o ar contido no conjunto atinge de temperatura, o abastecimento de ar é interrompido. Neste instante, o cilindro-pistão possui de ar. Determine o trabalho realizado pelo ar ao empurrar o pistão.
Passo 1
Galera, esse exercício de regime transiente falou falou, mas quais dados ele nos deu?

Resumindo tudo, o enunciado disse que ar a entra em um conjunto cilindro pistão inicialmente sem ar (massa de ar ) até o conjunto ficar com uma massa de ar a temperatura . Nesse enchimento, o ar realiza um trabalho no pistão que o enunciado pediu para a gente achar. A figura abaixo ilustra esses dados.
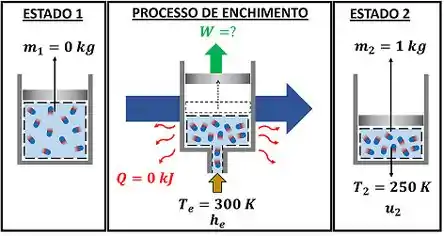
O calor trocado entre o ar e o ambiente vale zero, porque o conjunto cilindro-pistão está isolado termicamente.
Para achar o valor do trabalho realizado pelo ar sobre o pistão, temos que aplicar a lei de conservação de energia no conjunto.
Substituindo e nessa equação, achamos uma fórmula pra .
Ou seja, temos que achar , e pra calcular ! Acharemos as três na próxima etapa!
Passo 2
Achamos e , usando a fórmula de energia interna e entalpia de gases perfeitos com calores específicos constantes. Essas fórmulas são mostradas abaixo.
onde é o calor específico a pressão constante do ar que vale e é o calor específico a volume constante do ar que vale .
Substituindo os valores, encontramos:
A quantidade de massa que o conjunto recebe de ar é igual à massa de ar que o cilindro-pistão passou a ter depois do abastecimento menos a quantidade de ar que o conjunto tinha antes. Logo:
Substituindo os valores na fórmula de :
Boaaaaaa! Achamos o trabalho realizado pelo ar! Pode soltar os fogos e comemorar!
Resposta
Exercício Resolvido #2
Elaboração própria
Um conjunto cilindro-pistão termicamente isolado está inicialmente evacuado e começa a ser preenchido com ar a . Quando o ar contido no conjunto atinge de temperatura, o abastecimento de ar é interrompido. Neste instante, o ar do cilindro-pistão ocupa um volume igual a e possui uma pressão de . Determine o trabalho realizado pelo ar ao empurrar o pistão.
Passo 1
Galera, pra entender o enunciado, vamos resumir tudo! Ar a entra em um conjunto cilindro pistão inicialmente sem ar (massa inicial ) até o conjunto ficar com ar a , e ocupar um volume . Nesse enchimento, o ar realiza um trabalho que precisamos calcular. A figura abaixo ilustra esses dados.
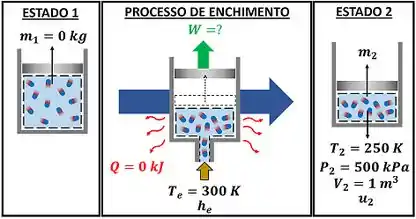
O calor trocado entre o ar e o ambiente vale zero, porque o conjunto cilindro-pistão está isolado termicamente.
Para achar o valor do trabalho realizado pelo ar sobre o pistão, temos que aplicar a lei de conservação de energia no conjunto.
Substituindo e nessa equação, achamos uma fórmula pra .
Ou seja, temos que achar , , e pra calcular ! Acharemos e na próxima etapa!
Passo 2
Achamos e , usando a fórmula de energia interna e entalpia de gases perfeitos com calores específicos constantes. Essas fórmulas são mostradas abaixo.
onde é o calor específico a pressão constante do ar que vale e é o calor específico a volume constante do ar que vale .
Substituindo os valores, encontramos:
Agora só falta achar e pra calcular . Então partiu fazer isso no passo seguinte!
Passo 3
Nós podemos calcular a massa de ar que o cilindro-pistão passa a ter depois de ser abastecido, usando a equação de gases perfeitos no estado 2 do ar.
onde é a constante de gás do ar que vale .
Substituindo os valores na fórmula de , achamos:
A quantidade de massa que o conjunto recebe de ar é igual à massa de ar que o cilindro-pistão passou a ter depois do abastecimento menos a quantidade de ar que o conjunto tinha antes. Logo:
Substituindo os valores na fórmula de :
Shoooooow! Calculamos o trabalho realizado pelo ar! Pode comemorar!
Resposta
Exercício Resolvido #3
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 173-6.119
A Fig. P6.119 mostra o esquema de uma turbina que é alimentada com a e . A descarga da turbina está ligada a um tanque com volume de , e que inicialmente está evacuado. A operação da turbina termina quando a pressão no tanque atinge . Nesta condição, a temperatura do no tanque é de . Admitindo que todos os processos são adiabáticos, determine o trabalho realizado pela turbina num processo de enchimento do tanque.
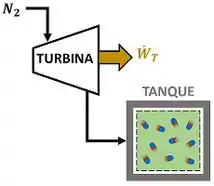
Passo 1
Pessoal, tudo joinha? Vamos resumir esse enunciado e entender o que ele nos deu de dado? Resumindo tudo, o enunciado disse que a e pressão passa pela turbina, gerando um trabalho desconhecido, e enche um tanque inicialmente sem (massa inicial ). O tanque para de encher, quando o alcança o estado 2 abaixo.
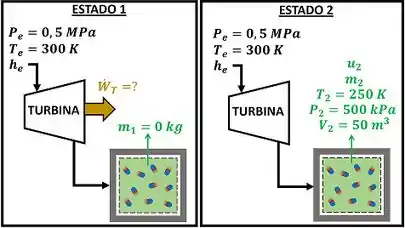
O calor trocado entre o e o ambiente vale zero, porque o enunciado diz que todos os processos são adiabáticos.
Para achar o valor do trabalho que foi pedido , temos que aplicar a lei de conservação de energia no conjunto formado pela turbina e pelo tanque.
Substituindo e nessa equação, achamos uma fórmula pra .
Ou seja, temos que achar , , e pra calcular ! Acharemos e na próxima etapa!
Passo 2
Achamos e , usando a fórmula de energia interna e entalpia de gases perfeitos com calores específicos constantes. Essas fórmulas são mostradas abaixo.
onde é o calor específico a pressão constante do que vale e é o calor específico a volume constante do que vale .
Substituindo os valores, encontramos:
Agora só falta achar e pra calcular . Então partiu fazer isso no passo seguinte!
Passo 3
Nós podemos calcular a massa de que o tanque passa a ter depois de ser abastecido, usando a equação de gases perfeitos no estado 2 de .
onde é a constante de gás do que vale .
Substituindo os valores na fórmula de , achamos:
A quantidade de massa que o tanque recebe de é igual à massa de que o tanque passou a ter depois do abastecimento menos a quantidade de que o tanque tinha antes. Logo:
Substituindo os valores na fórmula de :
Aaaaaaaaa, garot@! Conseguimos! Achamos o trabalho realizado pelo !
Resposta
Exercício Resolvido #4
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 172-6.109
Um tanque rígido e com volume de contém, inicialmente, a e . Uma válvula é aberta, lentamente, e o gás escapa vagarosamente do tanque até que a pressão atinja . Neste instante a válvula é fechada. Admitindo, para o gás que permanece no tanque, que o processo de esvaziamento pode ser modelado como uma expansão politrópica com expoente igual a , determine a massa final de no tanque e o calor transferido no processo.
Passo 1
Como vão, chuchus? Tudo bem? Bora fazer um exercício de processo em regime transiente?
O exercício quer saber quanto vale o calor que o do tanque troca com o ambiente durante o processo de esvaziamento do tanque.
A figura abaixo mostra alguns dados que temos pra calcular .
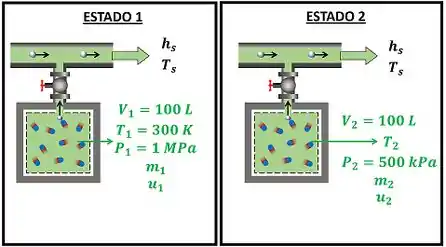
Através da figura, vemos que o do tanque estava no estado 1 e passa para o estado 2 depois de ser esvaziado de . e são a temperatura e a entalpia do que está escapando do tanque rígido. Para achar o valor do calor trocado , temos que aplicar a lei de conservação de energia no tanque.
Como o tanque é rígido, o não muda seu volume. Logo, o não realiza trabalho de movimento de fronteira. Em outras palavras, vale zero.
Subsituindo esse dado e reorganizando a equação, achamos uma fórmula pra .
Pra achar , temos que achar , , , , e . Vamos começar a fazer as contas, encontrando e no próximo passo.
Passo 2
Para encontrar , temos que usar a equação de energia interna para gases perfeitos com calor específico constante.
é o calor específico a volume constante de que vale .
Achamos o valor da massa de , usando a equação de gases perfeitos abaixo.
onde é a constante de gás do que vale .
Para usar essa equação, temos que converter de pra , multiplicando por . Além disso, temos que converter de litro pra , dividindo por .
Pronto, concluímos a primeira etapa pra achar ! No próximo passo vamos achar e !
Passo 3
Para encontrar , usamos novamente equação de energia interna para gases perfeitos com calor específico constante.
O problema é que ainda não conhecemos ! Pra achar essa temperatura , temos que usar a informação que o enunciado nos deu de que o esvaziamento é como se fosse um processo politrópico de expansão com expoente . Isso quer dizer que:
onde é o volume específico do antes do esvaziamento do tanque e é o volume específico do depois do esvaziamento do tanque. Usando a equação pevetê povotó, somos capazes de substituir e achar uma fórmula pra !
Substituindo isso na fórmula anterior:
Reorganizando essa equação:
Substituindo os valores:
Agora sim podemos usar a fórmula de !
Por fim, achamos através da equação de gases perfeitos.
Substituindo os valores:
Depois de achar todos esses valores, resta apenas encontrar e ! Partiu fazer isso no passo seguinte!
Passo 4
A quantidade de massa que o tanque perde de é igual à massa de que o tanque tinha antes do esvaziamento do tanque menos a massa de passou a ter depois do esvaziamento. Logo:
é encontrado usando novamente equação de energia interna para gases perfeitos com calor específico constante.
onde é o calor específico do que vale .
é a temperatura do que sai do tanque durante o esvaziamento. Como a temperatura do no tanque varia de a , a temperatura do que sai do tanque também varia de a . Logo, usaremos para o cálculo de uma temperatura média entre e .
Substituindo na equação de :
Usando todos os valores que descobrimos na fórmula de , achamos:
Aeeee! Demorou mas encontramos o que a gente tanto queria! Ponto pra gente!
Resposta
Exercício Resolvido #5
Elaboração própria
Um tanque rígido de aço, isolado, com contém ar a . A temperatura do ar é igual a . O tanque está ligado, através de uma ramificação com válvula, a uma linha onde ar escoa a e . A válvula é aberta, permitindo o escoamento de ar para o tanque, e só é fechada quando a pressão interna atinge . Determine a temperatura no instante em que a válvula é fechada.
Passo 1
E aí, galera! Tudo fluindo? Partiu fazer um exercício de processo em regime transiente?
O exercício quer saber quanto vale a temperatura do ar no tanque após ele ser abastecido com ar a e , fazendo o ar ficar com uma pressão de .
A figura abaixo mostra os dados que temos pra calcular .
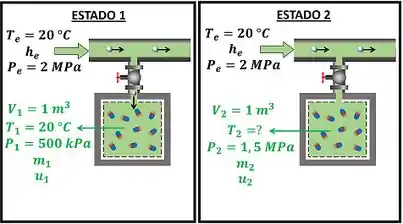
Através da figura, vemos que o ar do tanque estava no estado 1 e passa para o estado 2 depois de ser abastecido com ar. Para achar o valor da temperatura do ar após o abastecimento, temos que aplicar a lei de conservação de energia no tanque:
é o calor trocado entre o ar e o ambiente. Ele vale zero, porque o tanque está isolado. Além disso, como o tanque é rígido, o ar não muda seu volume. Logo, o ar não realiza trabalho de movimento de fronteira. Em outras palavras, vale zero. Subsituindo esses dados:
Até agora temos uma equação em que a temperatura que queremos não aparece. Nós fazemos aparecer, calculando as energias internas e e a entalpia através dos calores específicos, conforme mostrado pelas fórmulas abaixo.
onde é o calor específico a pressão constante do ar que vale e é o calor específico a volume constante do ar que vale .
Com todas essas informações em mãos, podemos começar a tentar a achar no próximo passo.
Passo 2
Para achar a temperatura através da lei de conservação de energia, temos que colocar todas as variáveis dessa equação em função de . Já conseguimos colocar , e em função de . Falta achar , usando as equações de gás perfeito nos estados 1 e 2 do ar.
onde é a constante de gás do ar que vale .
Para usar essa fórmula, precisamos converter de pra somando a .
Aplicando a equação de gases perfeitos no estado 2 do ar:
A quantidade de massa que o tanque recebe de ar é igual à massa de ar que o tanque passou a ter depois do abastecimento menos a quantidade de ar que o tanque tinha antes. Logo:
Agora sim podemos achar através da lei de conservação de energia.
Passo 3
Substituindo os termos em função de na equação de conservação de energia:
Multiplicando os dois lados da equação por :
Para usar essa fórmula, precisamos primeiro converter a pressão de pra , multiplicando por . Depois, convertemos e de pra , somando e a .
![]()
Aeeee! Conseguimos achar e acabar o exercício! :)
Resposta
Exercício Resolvido #6
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 172-6.110
Um recipiente rígido, inicialmente em vácuo, é carregado com água, proveniente de uma tubulação, a e . Admita que o processo de enchimento é adiabático e que o recipiente é lacrado quando a pressão interna for igual à da linha. Sabendo que a massa contida no recipiente após o término da operação de enchimento é igual a , determine a temperatura final do processo de enchimento e o volume do recipiente.
Passo 1
Oi gente! Animad@s pra fazer um exercício de processo em regime transiente?
O exercício quer saber quanto vale a temperatura da água no tanque após ele ser abastecido com água a e . Ele também quer saber quanto vale o volume do tanque. A figura abaixo mostra os dados que temos pra calcular e .
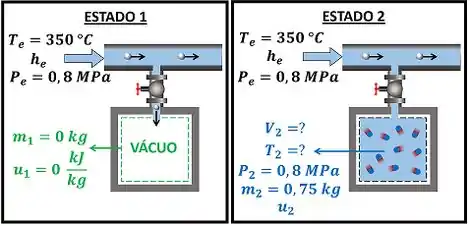
Através da figura, vemos que a água do tanque estava no estado 1 e passa para o estado 2 depois de ser abastecido com água. , e são a temperatura, a pressão e a entalpia da água que entra no tanque. Para achar o valor da temperatura da água após o abastecimento, temos que aplicar a lei de conservação de energia no tanque:
é o calor trocado entre a água e o ambiente. Ele vale zero, porque o processo de enchimento é adiabático. Além disso, como o tanque é rígido, a água do tanque não muda seu volume. Logo, a água não realiza trabalho de movimento de fronteira. Em outras palavras, vale zero. Subsituindo esses dados:
Além disso, como o tanque estava vazio no início do enchimento, a massa de água inicial no tanque vale zero, assim como a energia interna inicial da água no tanque.
Reorganizando essa equação, achamos uma fórmula para a energia interna que a água do tanque tem após o enchimento do tanque.
Com e , podemos usar a tabela de propriedades da água e achar o valor de !
No próximo passo acharemos e para conseguir calcular e encontrar através da tabela!
Passo 2
A quantidade de massa que o tanque recebe de água é igual à massa de água que o tanque passou a ter depois do abastecimento menos a quantidade de água que o tanque tinha antes. Logo:
Substituindo na fórmula de , descobrimos que:
é a entalpia específica do vapor d’água superaquecido a e que entra no tanque. A água está superaquecido, porque sua temperatura é maior que a temperatura de saturação de da água a pressão de .
Logo, achamos na tabela de vapor superaquecido da água a e .
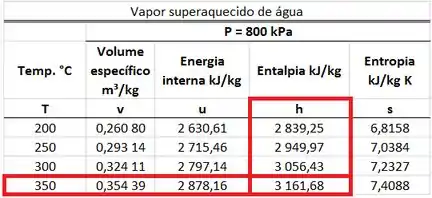
Agora sim podemos achar e no próximo passo.
Passo 3
Como é igual a , temos que vale:
Já sabemos que a pressão da água no tanque após o enchimento vale e que a energia interna da água após o enchimento do tanque vale . Com essas informações, somos capazes de determinar se a água é um vapor superaquecido ou é saturada, comparando com a energia interna do vapor saturado a .
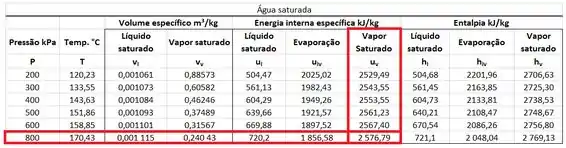
Comparando com , descobrimos que a energia interna é maior. Isso quer dizer que a água do tanque após o enchimento é um vapor superaquecido.
Logo, achamos interpolando a tabela de vapor superaquecido da água que tem e .
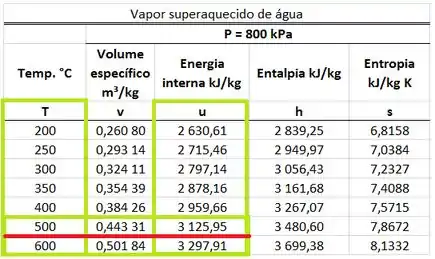
Oba! Achamos a primeira informação que o enunciado nos pediu! Agora, vamos calcular o volume do tanque!
Passo 4
O volume do tanque que a água ocupa após o enchimento pode ser calculado através da fórmula do volume específico do vapor superaquecido d’água.
Achamos o valor de , interpolando a tabela de vapor superaquecido d’água, usando o valor da energia interna que possuímos.
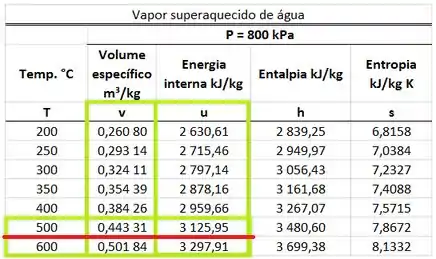
Substituindo na equação de , achamos:
Boaaaaa! Achamos a segunda e última informação que o enunciado nos pediu! Agora é só correr pro abraço!
Resposta
Exercício Resolvido #7
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 173-6.113
Um tanque rígido, com capacidade de , contém ar a e . Uma válvula do tanque é aberta e o ar escoa para fora do tanque até que a pressão atinja . Calor é transferido ao ar, de um reservatório térmico que apresenta temperatura igual a , durante todo o processo. Sabendo que a temperatura final do ar no tanque é , determine a transferência de calor no processo.
Passo 1
Oi, lind@s! Tudo sereno? Vamos direto pro que interessa?
O exercício quer saber quanto vale o calor que o ar do tanque troca com o ambiente durante o processo de esvaziamento do tanque.
A figura abaixo mostra alguns dados que temos pra calcular .
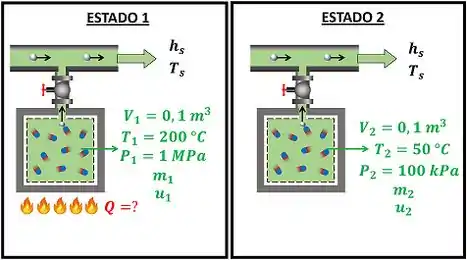
Através da figura, vemos que o ar o tanque estava no estado 1 e passa para o estado 2 depois de ser esvaziado. e são a temperatura e a entalpia do ar que está escapando do tanque rígido. Para achar o valor dado calor trocado , temos que aplicar a lei de conservação de energia no tanque.
Como o tanque é rígido, o ar não muda seu volume. Logo, ele não realiza trabalho de movimento de fronteira. Em outras palavras, vale zero.
Subsituindo esse dado e reorganizando a equação, achamos uma fórmula pra .
Pra achar , temos que achar , , , , e . Vamos começar a fazer as contas, encontrando e no próximo passo.
Passo 2
Para encontrar , temos que interpolar a tabela de gás perfeito do ar.
Antes disso, temos que converter a temperatura de pra , somando a .
Agora nós podemos ver quanto vale na tabela abaixo.
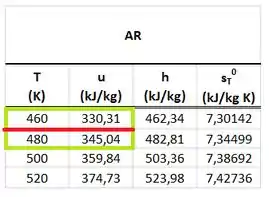
Achamos o valor da massa de ar, usando a equação de gases perfeitos abaixo.
onde é a constante de gás do ar que vale .
Para usar essa equação, temos que converter de pra , multiplicando por .
Pronto, concluímos a primeira etapa pra achar ! No próximo passo vamos achar e !
Passo 3
Para encontrar , temos que interpolar novamente a tabela de gás perfeito do ar.
Antes disso, temos que tomar aquele cuidado de converter a temperatura de pra , somando a .
está na tabela abaixo.
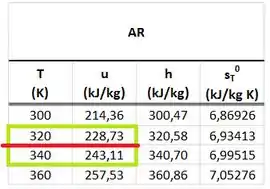
Achamos o valor da massa de ar, usando a equação de gases perfeitos abaixo.
Substituindo os valores que temos:
Depois de achar todos esses valores, resta apenas encontrar e ! Partiu fazer isso no passo seguinte!
Passo 4
A quantidade de massa que o tanque perde de ar é igual à massa de ar que o tanque tinha antes do esvaziamento do tanque menos a massa de passou a ter depois do esvaziamento. Logo:
é a entalpia do ar que sai do tanque durante o esvaziamento. Como a temperatura do ar no tanque varia de a , a entalpia do ar que sai do tanque também varia de a . Logo, usaremos para o cálculo de uma entalpia média entre e .
e são encontrados interpolando a mesma tabela que encontramos e para as temperaturas e .
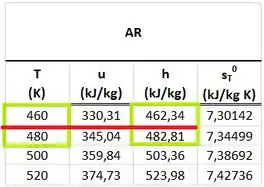
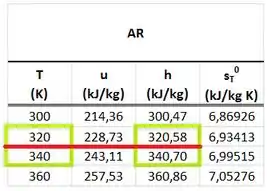
Com esses dados vemos que vale:
Substituindo todos os valores que achamos na fórmula de :
Até que enfiiim! Demorou mas encontramos o que a gente tanto suou pra achar!
Resposta
Exercício Resolvido #8
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 173-6.116
Inicialmente, um conjunto cilindro-pistão que opera a pressão constante, contém de água a e . Existe no conjunto cilindro-pistão uma válvula que pode descarregar a água contida no conjunto na atmosfera . Esta válvula é aberta e só é fechada quando a massa contida no conjunto se torna igual a . Admitindo que o processo é adiabático, que a temperatura da água é sempre uniforme, determine a velocidade de descarga da água e o trabalho realizado no processo.
Passo 1
Oier, fofões! Empolgad@s pra fazer um exercício de processo em regime transiente?
A primeira informação que vocês precisam entender é que, quando o enunciado diz que a temperatura da água é uniforme, ele quer dizer que a temperatura da água permanece constante durante todo processo de esvaziamento do cilindro-pistão.

O exercício quer saber primeiro quanto vale o trabalho realizado sobre a água do cilindro durante a saída de água a pressão do conjunto cilindro-pistão. Depois, a questão quer que a gente descubra a velocidade de saída da água.
A figura abaixo mostra os dados que temos pra calcular e .
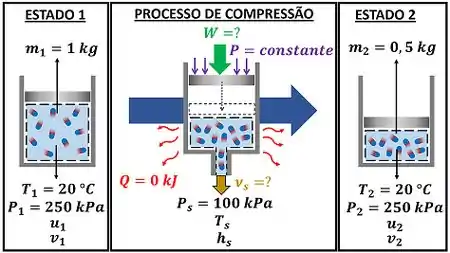
vale zero, porque o enunciado diz que o processo é adiabático.
Para achar o valor do trabalho , vamos usar a fórmula de trabalho de fronteira a pressão constante, porque o enunciado informa que o conjunto cilindro-pistão opera a pressão constante.
onde é o volume que a água ocupa no cilindro depois do esvaziamento e é o volume que a água ocupava no cilindro antes do esvaziamento.
Pra encontrar a velocidade da água saindo do cilindro, temos que aplicar a lei de conservação de energia no conjunto cilindro-pistão.
Ou seja, pra encontrar , temos que achar antes. Por isso, iniciaremos as contas determinando no próximo passo.
Passo 2
Pra encontrar os volumes que a água ocupava e que a água passou a ocupar e determinar , temos que usar as equações dos volume específicos (que a água tinha) e (que a água passou a ter).
Isso quer dizer que pra achar e , precisamos achar e . é o volume específico da água líquida comprimida a e e é o volume específico da água líquida comprimida a e . Se você observar bem, verá que as temperaturas e pressões são iguais. Logo, o estado 1 é igual ao estado 2 da água e temos que:
Ou seja, vamos obter os dois volumes específicos ao mesmo tempo, usando a tabela de propriedades da água. Como não existe uma tabela de água líquida comprimida para uma pressão tão baixa quanto , assumimos que o volume específico da água líquida comprimida, é igual ao volume específico da água líquida saturada a .
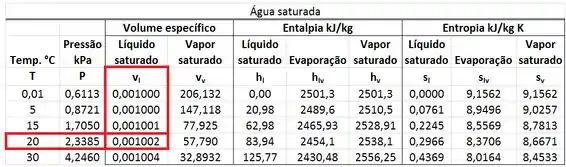
Substituindo essa informação nas equações de e :
Agora podemos achar o valor do trabalho , substituindo e na fórmula de .
Com esse valor em mão, só falta achar , , e pra encontrar . Acharemos esses valores no próximo passo.
Passo 3
A quantidade de massa que o cilindro-pistão perde de água é igual à massa de água que o cilindro pistão tinha antes do esvaziamento menos a quantidade de água que o cilindro-pistão passou a ter. Logo:
As energias internas específicas e são iguais, porque vimos que os estados 1 e 2 são iguais.
Vamos obter e , usando a tabela de propriedades da água. Como não existe uma tabela de água líquida comprimida para uma pressão tão baixa quanto , assumimos que a energia interna específica da água líquida comprimida, é igual à energia interna específica da água líquida saturada a .
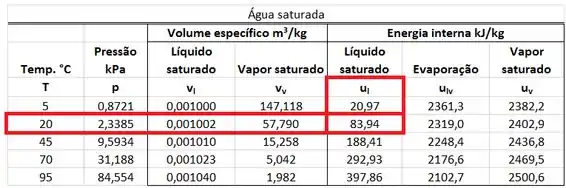
Para encontar a entalpia da água que sai do cilindro, temos que notar que a temperatura da água que sai do cilindro é igua à temperatura da água que está dentro do cilindro.
Isso significa que a água que sai do cilindro é um líquido comprimido a e . Como não existe uma tabela de água líquida comprimida para uma pressão tão baixa quanto , assumimos que a entalpia específica da água líquida comprimida , é igual à entalpia específica da água líquida saturada a .
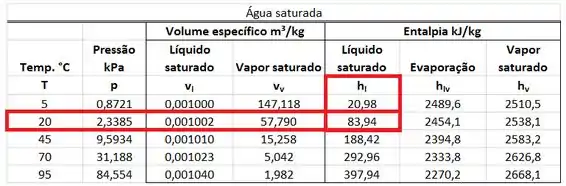
Antes de substituir todos os valores na fórmula de , precisamos converter de pra , multiplicando por e precisamos converter , e de pra , multiplicando esses três termos por .
Uhuuuul! Depois de tanto sufoco conseguimos finalmente achar tudo o que o enunciado pediu pra gente!