Trocadores de Calor
Teoria
O que é um trocador de calor?
As vezes o dia está tão quente, que ligar o ventilador não é o suficiente para se refrescar! Nessa situação, só o vento geladinho de um ar condicionado resolve! Mas por que o vento do ar condicionado é mais frio que o vento do ventilador, se essas duas máquinas usam o mesmo ar do ambiente para tirar nosso calor?
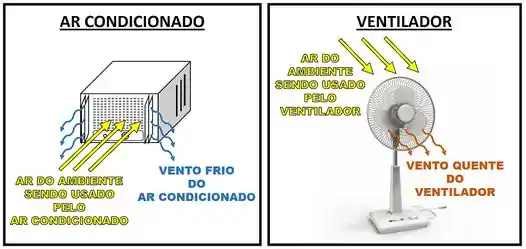
Em outras palavras, que tipo de equipamento dentro do ar condicionado consegue absorver o calor do ar quente e diminuir sua temperatura? Esse equipamento se chama trocador de calor! No trocador de calor do ar condicionado, o calor do ar quente é absorvido por um fluido muito frio! Ou seja, o calor sai do ar quente e atravessa a parede do tubo de fluido frio!
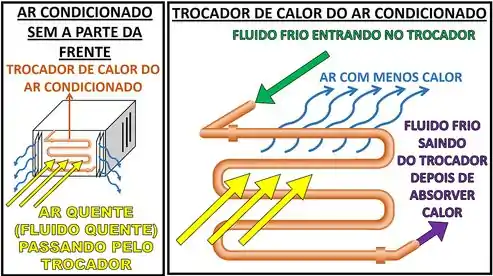
O trocador de calor é o equipamento, onde o fluido mais quente (gás, vapor ou líquido) passa calor para o fluido mais frio (gás, vapor ou líquido)! Ele é um equipamento com tubos. Em alguns passa o fluido quente. Em outros passa o fluido frio. O calor é transferido de um fluido para o outro através de uma parede que os separa!
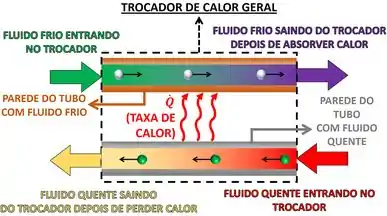
Os tipos de trocador de calor
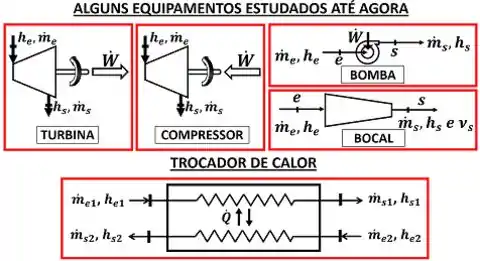
Muitas vezes, os enunciados dos exercícios não falam diretamente que a questão é sobre um trocador de calor. Geralmente, eles chamam o trocador de calor pelo nome do seu tipo. Por exemplo, o trocador de calor que resfria o ar do ar condicionado é chamado de evaporador. Esse é só um tipo de trocador! Existem outros que são mostrados pela figura abaixo.
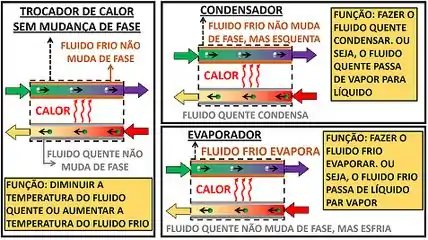
Vemos na figura acima que existe um tipo de trocador de calor para cada função diferente. O evaporador é usado para evaporar um fluido. O condensador é usado para condensar um fluido. E os trocadores comuns são usados para diminuir ou aumentar a temperatura de um fluido, sem fazer ele mudar de fase.
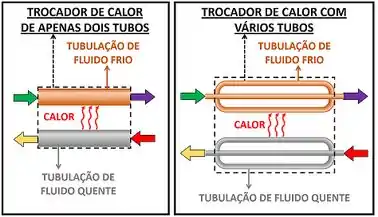
Além disso, vemos na figura acima que a troca de calor pode acontecer entre dois tubos ou entre vários tubos que transportam os fluidos!
Essa variedade de tipos pode assustar a gente! Se existem vários tipos diferentes de trocadores de calor, vamos precisar gravar uma fórmula da primeira lei para cada um deles?
Calma que isso não é verdade! Veremos o motivo a seguir!
Os trocadores são diferentes mas suas fórmulas de primeira lei são iguais!
Apesar de existirem vários tipos de trocador de calor, todos eles funcionam de forma igual ao trocador mais simples de dois tubos. É por isso que usamos a mesma forma da primeira lei para todos eles! Além disso, todos eles são representados pelo mesmo desenho simples em questões de trocadores de calor.
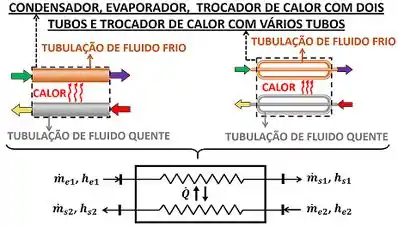
Isso significa que, na maioria dos casos, nós usamos a mesma fórmula para calcular a taxa de transferência de calor do fluido mais quente para o fluido mais frio ! Mas atenção! Para conseguir calcular , precisamos usar a primeira lei da termodinâmica em apenas um dos fluidos! Por enquanto, não vamos usar a primeira lei para o equipamento inteiro!
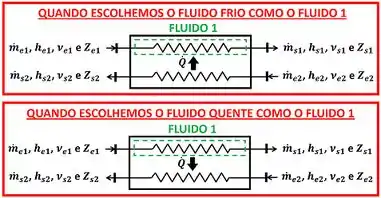
Isso quer dizer que temos que nos focar em apenas um dos fluidos que trocam calor para conseguir criar uma fórmula para ! Vamos chamar esse fluido que escolhemos de fluido 1! O fluido 1 tem vazão de entrada igual a e vazão de saída igual a . O fluido 2 tem vazão de entrada igual a e vazão de saída igual a .
Primeira lei para um fluido do trocador de calor funcionando em regime permanente
Para conseguir calcular , temos que lembrar que os fluidos não realizam nem sofrem trabalho dentro do trocador . Além disso, podemos fazer algumas simplificações na primeira lei. Sua forma completa é bem grande e não é prática. Simplificar vai ajudar a gente!
A primeira lei do fluido 1 sem simplificação tem a forma abaixo.
Além de considerar , podemos considerar que outros termos da primeira lei também valem zero! As variações de energia cinética e potencial do fluido normalmente são pequenas, porque o fluido não varia muito sua velocidade nem varia muito sua altitude ! Por causa disso, elas podem ser desprezadas! Com isso a primeira lei vira:
Se o fluido 1 for o fluido frio do trocador, a taxa de calor será positiva , porque o fluido ganhará calor. Se o fluido 1 for o fluido quente do trocador, a taxa de calor será negativa , porque o fluido perderá calor.
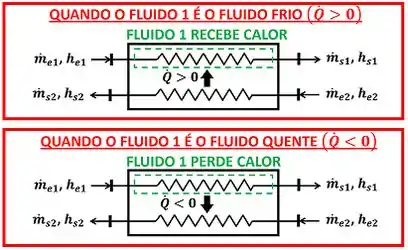
onde:
- é a vazão mássica do fluido 1 que está entrando no trocador e é a vazão mássica do fluido 1 que está saindo no trocador. Suas unidades no Sistema Internacional (S.I.) são o quilograma por segundo ;
- é a entalpia específica do fluido 1, quando ele está entrando no trocador e é a entalpia específica do fluido 1, quando ele está saindo do trocador. Elas são medidas em joule por quilograma segundo o Sistema Internacional (S.I.);
- é a taxa de calor trocado entre o fluido mais quente e o fluido mais frio.
Como descobrir as pressões de entrada e saída de um fluido?
Para calcular as entalpias específicas ( e ), nós precisamos saber os valores de pressão do fluido. Ele pode ter uma pressão, quando está entrando no trocador de calor e outra, quando está saindo do equipamento ! No entanto, na maioria dos problemas, o enunciado só informa uma dessas pressões. Como nós podemos descobrir o valor da outra que falta?
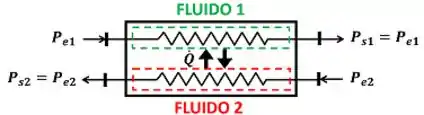
Na maioria dos casos, a pressão do fluido não muda conforme ele passa pelos tubos do trocador de calor. Por causa disso, podemos considerar que a pressão de saída do fluido é igual à pressão de entrada do fluido . Isso significa que a pressão de um fluido, geralmente, permanece constante durante todo o processo de troca de calor!
Isso serve tanto para o fluido 1 quanto para o fluido 2. Por isso, essa nova simplificação pode facilitar muito a nossa vida! No entanto, ela não é a única variável do fluido que permanece constante durante a troca de calor! As vazões mássicas do fluido também são constantes e precisamos saber disso para resolver as questões de prova!
Conservação de massa do trocador de calor
O trocador de calor é diferente de todos os outros equipamentos que estudamos até agora. Ele não tem apenas uma vazão mássica entrando e outra saindo. Geralmente, o trocador de calor de exercícios de termodinâmica têm duas vazões mássicas entrando e duas vazões mássicas saindo. Nesse caso, como fica a equação de conservação de massa do trocador?
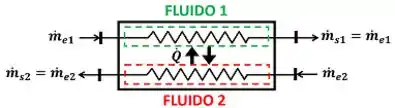
Vemos na imagem acima que o fluido 1 e o fluido 2 não se misturam durante a troca de calor. Em outras palavras, suas vazões não aumentam nem diminuem ao longo do processo! Elas ficam constantes! Portanto:
Primeira lei para o trocador de calor inteiro funcionando em regime permanente
Nós aprendemos a escrever a primeira lei da termodinâmica, focando em apenas um dos fluidos (fluido 1). Como será que fica essa equação, se a gente resolver incluir os dois fluidos (fluido 1 e fluido 2) nela? Os equipamentos até agora só tinham uma vazão entrando e outra saindo . Como fica a equação, quando existem duas vazões mássicas entrando ( e ) e duas saindo ( e )?
Para escrever essa equação, temos que lembrar que vale zero e as variações de energia cinética e potencial dos dois fluidos são desprezíveis. Por causa disso, a primeira lei para o trocador de calor inteiro em regime permanente vira:
onde é a entalpia específica do fluido 2, quando ele está entrando no trocador e é a entalpia específica do fluido 2, quando ele está saindo do trocador.
Mas por que o não aparece nessa equação, se existe uma taxa de calor que é trocada dentro do trocador de calor?
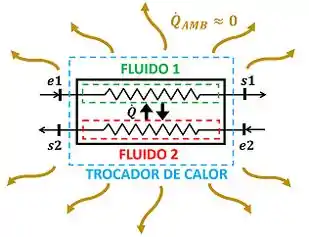
Porque na primeira lei da termodinâmica não aparecem as taxas de calor que são trocadas dentro do volume de controle! Só aparecem as taxas de calor que são trocadas entre o volume de controle e o que está fora dele. O que está fora do trocador de calor é o ambiente. Mas ele quase não troca calor com o ambiente . Toda troca de calor desse equipamento acontece dentro dele! Por isso ela não aparece na equação!
Os tipos de trocador de calor
Os trocadores são diferentes mas suas fórmulas de primeira lei são iguais!
Primeira lei para um fluido do trocador de calor funcionando em regime permanente
Como descobrir as pressões de entrada P e 1 e saída P s 1 de um fluido?
Conservação de massa do trocador de calor
Primeira lei para o trocador de calor inteiro funcionando em regime permanente
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
de um líquido frio passa por um trocador de calor a cada segundo. Esse líquido recebe calor a uma taxa de ao atravessar o trocador. Determine a variação da entalpia específica do líquido, considerando que ele escoa em regime permanente através da trocador de calor.
Passo 1
O exercício pede para a gente calcular a variação de entalpia específica do líquido frio que atravessa o trocador. A figura baixo mostra todos os dados fornecidos pelo enunciado para calcular esse valor.
e são as vazões mássicas do liquido entrando e saindo do trocador respectivamente. Elas são iguais, porque a conservação de massa para um escoamento em regime permanente diz que:
é a taxa de calor que o líquido frio recebe durante sua passagem pelo trocador.
Agora que sabemos o que os dados significam, vamos aprender a calcular .
Passo 2
é calculado a partir da primeira lei para trocadores de calor em regime permanente. Vale lembrar que, nesse caso, nós estamos estudando apenas uma corrente que passa pelo trocador. Estamos estudando a corrente do fluido mais frio. Logo, ele recebe calor! Por isso, é positivo.
Como e são iguais, nós podemos colocar qualquer uma dessas vazões em evidência.
Vamos iniciar as contas no próximo passo!
Passo 3
Resposta
Exercício Resolvido #2
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 167-6.68
A vazão de ar num ar condicionado é . O equipamento é alimentado com ar a e e descarrega o fluido a e . Determine a taxa de transferência de calor que ocorre no escoamento do ar.
Passo 1
O exercício pede para a gente calcular a taxa de toca de calor que ocorre dentro do ar condicionado. A figura baixo mostra todos os dados fornecidos pelo enunciado para calcular esse valor.
é a vazão mássica do ar entrando e saindo do ar condicionado. é a temperatura do ar entrando no ar condicionado e é a temperatura do ar saindo do ar condicionado. é a pressão do ar entrando no ar condicionado e é a pressão do ar saindo do ar condicionado.
Agora que sabemos o que os dados significam, vamos aprender a calcular .
Passo 2
é calculado a partir da primeira lei para trocadores de calor em regime permanente. Vale lembrar que, nesse caso, nós estamos estudando apenas uma corrente que passa pelo trocador. Estamos estudando a corrente de ar.
Na fórmula acima, podemos ver que para calcular o valor de , precisamos encontrar o valor da diferença entre as entalpias específicas do ar e .
Como o ar pode ser considerado um gás perfeito, pode ser calculado através da fórmula abaixo.
onde é o calor específico do ar a pressão constante. Ele vale:
Atenção! As duas temperaturas presentes nessa fórmula tem que estar em kelvin . No entanto, estamos apenas interessados nas diferenças de temperaturas. Além disso, a diferença de temperatura em kelvin é igual à diferença de temperatura em grau Celsius . Por isso, podemos substituir os valores das temperaturas em grau Celsius na fórmula!
Substituindo essa fórmula na equação da primeira lei, encontramos:
Sabendo disso, podemos iniciar as contas!
Passo 3
Resposta
Exercício Resolvido #3
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 163-6.23
Uma caldeira é alimentada com de água líquida a e e descarrega vapor d’água a e . Determine as seções de escoamento na alimentação e descarga da caldeira de modo que as velocidades dos escoamentos sejam menores do que .
Passo 1
O exercício pede para a gente calcular a área pela qual a água passa para entrar na caldeira e a área pela qual a água passa para sair da caldeira. A figura baixo mostra todos os dados fornecidos pelo enunciado para calcular esses valores.
é a vazão mássica de água entrando e saindo da caldeira. é a temperatura da água entrando na caldeira e é a temperatura da água saindo da caldeira. é a pressão da água entrando na caldeira e é a pressão da água saindo da caldeira. é a velocidade da água entrando na caldeira e é a velocidade da água saindo da caldeira.
Agora que sabemos o que os dados significam, vamos aprender a calcular e .
Passo 2
Para calcular e precisamos usar a fórmula da vazão mássica abaixo. Ela mostra que a massa especifica multplicada pela velocidade do escoamento e pela área de passagem da água é igual à vazão mássica . Essa fórmula serve tanto para a vazão entrando na caldeira quanto para a vazão saindo da caldeira.
onde é a massa específica da água entrando na caldeira e é a massa específica da água saindo da caldeira.
Lembrando que é o inverso do volume específico da água e é o inverso do volume específico da água , conseguimos criar as fórmulas para calcular e .
Calcularemos as duas áreas usando o valor limite das velocidades para saber as áreas de escoamento mínimas.
As fórmulas acima mostram que para calcular e precisamos dos valores de e . Encontraremos esses valores no próximo passo.
Passo 3
A água que entra na caldeira é um líquido comprimido a e a . Portanto, o valor do volume específico desse líquido é encontrado na tabela de líquido comprimido da água. Ele está na mesma linha que a temperatura de e na mesma coluna que .
A água que sai da caldeira é um vapor superaquecido a e a . Portanto, o valor do volume específico desse vapor é encontrado na tabela de vapor superaquecido da água. Ele está na mesma linha que a temperatura de e na mesma coluna que .
Com esses dois valores em mãos, nós podemos iniciar as contas!
Passo 4
Antes de usar as fórmulas, nós precisamos converter a vazão mássica de para .
Resposta
Exercício Resolvido #4
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 167-6.65
O trocador de calor utilizado numa central de água gelada é alimentado com de água a e e descarrega a água a . Determine a taxa de transferência de calor da água para o fluido refrigerante neste trocador de calor.
Passo 1
O exercício pede para a gente calcular a taxa de calor que sai da água e vai para o fluido refrigerante. A figura baixo mostra todos os dados fornecidos pelo enunciado para calcular esse valor.
é a vazão mássica de água entrando e saindo do trocador de calor. é a temperatura da água entrando no trocador de calor e é a temperatura da água saindo do trocador de calor. é a pressão da água entrando no trocador de calor e é a pressão da água saindo do trocador de calor.
Repare que o enunciado só fornece a pressão de entrada da água. Como poderíamos saber a pressão de saída ? Quando a questão não fala nada dessa pressão de saída da água, ela é igual à pressão de entrada !
Agora que sabemos o que os dados significam, vamos aprender a calcular .
Passo 2
é calculado a partir da primeira lei para trocadores de calor em regime permanente. Vale lembrar que, nesse caso, nós estamos estudando apenas uma corrente que passa pelo trocador. Estamos estudando a corrente de água. A primeira lei para essa corrente é:
Na fórmula acima, podemos ver que para calcular o valor de , precisamos encontrar o valor das entalpias específicas da água e . Faremos isso no próximo passo!
Passo 3
A corrente de água entrando no trocador de calor e a corrente de água saindo do trocador de calor são líquidos comprimidos, porque suas temperaturas ( e ) são menores que a temperatura de saturação a de pressão. Isso quer dizer que a gente teria que encontrar e em uma tabela de líquido comprimido da água!
No entanto, geralmente não temos a disposição uma tabela de líquido comprimido da água para uma pressão tão baixa quanto . Para contornar esse problema, nós podemos considerar a entalpia igual à entalpia do líquido saturado a e a entalpia igual à entalpia do líquido saturado a . Esses valores estão na tabela de saturação da água.
Com esses valores em mãos nós já podemos iniciar as contas!
Passo 4
Resposta
Exercício Resolvido #5
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 167-6.66
Uma caldeira, que opera em regime permanente, é alimentada com de nitrogênio líquido a . A caldeira descarrega o nitrogênio como vapor saturado a e alimenta um superaquecedor. Sabendo que todos os processos ocorrem em regime permanente e que o superaquecedor descarrega nitrogênio a e , determine as taxas de transferência de calor na caldeira e no superaquecedor.
Passo 1
O exercício pede para a gente calcular a taxa de toca de calor que o nitrogênio troca dentro da caldeira e também a taxa de calor que o nitrogênio troca dentro do superaquecedor. Ou seja, esse exercício envolve dois trocadores de calor: a caldeira e o superaquecedor. A figura baixo mostra todos os dados fornecidos pelo enunciado para calcular esses valores.
é a vazão mássica de nitrogênio que passa pela caldeira e passa pelo superaquecedor. é a temperatura do nitrogênio saindo do superaquecedor. é a pressão do nitrogênio entrando na caldeira, é a pressão do nitrogênio saindo da caldeira e entrando no superaquecedor e é a pressão do nitrogênio saindo do superaquecedor.
é o título do nitrogênio entrando na caldeira. Ele vale , porque o nitrogênio entra na caldeira como líquido saturado. O enunciado não informa isso, mas quando o nitrogênio está no estado líquido, ele geralmente está saturado. é o título do nitrogênio saindo da caldeira e entrando no superaquecedor. Ele vale , porque o nitrogênio entra na caldeira como vapor saturado.
Agora que sabemos o que os dados significam, vamos aprender a calcular .
Passo 2
é calculado a partir da primeira lei para trocadores de calor em regime permanente aplicada à caldeira. Vale lembrar que, nesse caso, nós estamos estudando apenas uma corrente que passa pela caldeira. Estamos estudando a corrente de nitrogênio. A primeira lei para essa corrente da caldeira é:
é calculado a partir da primeira lei para trocadores de calor em regime permanente aplicada ao superaquecedor. Vale lembrar que, nesse caso, nós estamos estudando apenas uma corrente que passa pelo superaquecedor. Estamos estudando a corrente de nitrogênio. A primeira lei para essa corrente da caldeira é:
Nas fórmulas acima, podemos ver que para calcular e , precisamos encontrar o valor das entalpias específicas do nitrogênio , e . Faremos isso no próximo passo!
Passo 3
A corrente de nitrogênio entrando na caldeira é um líquido saturado a . Logo, o valor da sua entalpia específica é encontrado na tabela de saturação do nitrogênio. Ele é a entalpia específica do líquido saturado a . No entanto, não existe uma linha para a pressão de na tabela de saturação. Por isso teremos que interpolar esse valor!
A corrente de nitrogênio saindo da caldeira é um vapor saturado a . Logo, o valor da sua entalpia específica é encontrado na tabela de saturação do nitrogênio. Ele é a entalpia específica do vapor saturado a . No entanto, não existe uma linha para a pressão de na tabela de saturação. Por isso teremos que interpolar esse valor!
A corrente de nitrogênio saindo do superaquecedor é um vapor superaquecido a . Logo, o valor da sua entalpia específica é encontrado na tabela de nitrogênio superaquecido. Ele está na mesma linha que a temperatura de e na mesma coluna que .
Com esses valores em mãos nós já podemos iniciar as contas!
Passo 4
Resposta
Exercício Resolvido #6
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 169-6.86
A Fig. P6.86 mostra o esquema de um trocador de calor utilizado para resfriar o ar, a pressão constante e igual a , de a . A água de resfriamento entra no equipamento a e . Se a água deixa o trocador como vapor saturado, calcule a relação entre as vazões de água e ar .
Passo 1
O enunciado pede que a gente calcule a divisão entre a vazão mássica de água que passa pelo trocador de calor e a vazão mássica de ar que passa pelo trocador de calor. A figura abaixo mostra todos os dados que o enunciado nos informa para calcular essa divisão .
é a temperatura da água entrando no trocador de calor e é a temperatura da água saindo do trocador de calor. é a temperatura do ar entrando no trocador de calor e é a temperatura do ar saindo do trocador de calor. é a pressão da água entrando no trocador de calor e é a pressão da água saindo do trocador de calor. é a pressão do ar entrando no trocador de calor e é a pressão do ar saindo do trocador de calor. é o título da água saindo do trocador de calor. Ele vale , porque é um vapor saturado!
Agora que sabemos o que cada dado significa, vamos aprender a calcular .
Passo 2
pode ser calculado através da equação de primeira lei para um trocador de calor incluindo duas correntes: uma de ar quente e outra de água de resfriamento. ATENÇÃO! A forma dessa equação não possui o termo de taxa de troca de calor!
onde é a entalpia específica do ar quente entrando no trocador de calor. é a entalpia específica do ar quente saindo do trocador de calor. é a entalpia específica da água de resfriamento entrando no trocador de calor. é a entalpia específica da água de resfriamento saindo do trocador de calor.
A fórmula de cima mostra que para calcular precisamos encontrar , , e . Vamos encontar a diferença de entalpias do ar no próximo passo.
Passo 3
O ar pode ser tratado como gás ideal. Por conta disso, pode ser calculado através da fórmula abaixo.
onde é o calor específico do ar a pressão constante. Ele vale:
Substituindo essa fórmula na fórmula de , encontramos.
Antes da gente aprender a encontrar a entalpia da água de resfriamento, temos que aprender a encontrar a pressão da água de resfriamento. Nós vamos aprender a descobrir esse valor na próxima etapa!
Passo 4
Quando a questão fala o valor da pressão da vazão que entra no trocador, mas não fala quanto vale a pressão na saída, a pressão de saída é igual à pressão de entrada. No caso da água de resfriamento, a pressão de entrada vale . Como a pressão de saída da água de resfriamento é igual a , vale:
Conhecendo esse valor, podemos seguir para a etapa de encontrar e .
Passo 5
A vazão de entrada da água de resfriamento está a e tem temperatura menor que a temperatura de saturação da água a . Isso significa que essa vazão é um líquido comprimido. No entanto, não existe tabela de líquido comprimido para . Por isso, consideraremos como a entalpia do líquido saturado a . Encontramos esse valor na tabela de saturação da água.
O enunciado diz que a vazão de saída da água é um vapor superaquecido. Logo, podemos encontrar a entalpia na tabela de saturação da água. Esse valor está na mesma linha da pressão de (que é igual a ) e na mesma coluna que a entalpia do vapor saturado .
Depois de aprender todas essas informações, podemos iniciar as contas!
Passo 6
Resposta
Exercício Resolvido #7
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 169-6.84
A Fig. P6.84 mostra o esboço de um condensador não misturado (trocador de calor) que é alimentado com de água a e e descarrega líquido saturado a . O fluido de resfriamento é água obtida num lago a e que retorna, ao mesmo tempo, a . Sabendo que a superfície externa do condensador é isolada, calcule a vazão da água de resfriamento.
Passo 1
O enunciado quer saber qual vale a vazão mássica de água do lago ( e ) que é usada para resfriar uma outra corrente de água. A figura abaixo mostra todos os dados que o enunciado nos informa para calcular essa vazão.
e são a vazão de água quente que passa pelo trocador de calor. As duas têm o mesmo valor porque o escoamento acontece em regime permanente, segundo a fórmula abaixo.
e são a vazão de água de resfriamento do lago que passa pelo trocador de calor. As duas também têm o mesmo valor porque o escoamento acontece em regime permanente, segundo a fórmula abaixo.
é a temperatura da água quente entrando no trocador de calor. é a temperatura da água de resfriamento entrando no trocador de calor. é a temperatura da água de resfriamento saindo do trocador de calor. é a pressão da água quente entrando no trocador de calor. é a temperatura da água quente saindo do trocador de calor. é o titulo da água quente saindo do trocador de calor. Ele vale , porque a água sai do trocador como líquido saturado.
Agora que sabemos o que cada dado significa, vamos aprender a calcular .
Passo 2
pode ser calculado através da equação de primeira lei para um trocador de calor incluindo duas correntes: uma de água quente e outra de água de resfriamento. ATENÇÃO! A forma dessa equação não possui o termo de taxa de troca de calor!
onde é a entalpia específica da água quente entrando no trocador de calor. é a entalpia específica da água quente saindo do trocador de calor. é a entalpia específica da água de resfriamento entrando no trocador de calor. é a entalpia específica da água de resfriamento saindo do trocador de calor.
A fórmula de cima mostra que para calcular precisamos encontrar , , e . Vamos encontar as entalpia e da água quente no próximo passo.
Passo 3
A vazão de água quente é um vapor superaquecido a e a . Logo, para encontar a entalpia , temos que usar a tabela de vapor superaquecido da água. Esse valor está na mesma linha da temperatura de e na mesma coluna da entalpia .
A vazão de água quente é um vapor saturado a . Logo, para encontar a entalpia , temos que usar a tabela de saturação da água. Esse valor está na mesma linha da pressão de e na mesma coluna da entalpia específica do líquido saturado .
Antes da gente aprender a encontrar as entalpias e da água de resfriamento, temos que aprender a encontrar as pressões e da água de resfriamento. é a pressão da água do lago entrando no trocador e é a pressão da água do lago saindo do trocador. Nós vamos aprender a descobrir esses dois valores na próxima etapa!
Passo 4
A vazão de água de resfriamento vem do lago. Como o lago está a pressão atmosférica de aproximadamente , a vazão também está a .
A vazão de água de resfriamento é despejado de volta no lago. Ou seja, essa vazão também está em contato com o lago que está a pressão atmosférica. Por causa disso, também podemos considerar que a vazão está a pressão atmosférica.
Conhecendo esses dois valores, podemos seguir para a etapa de encontrar e .
Passo 5
As vazões e estão a e têm temperaturas menores que a temperatura de saturação da água a . Isso significa que as vazões e são líquidos comprimidos. No entanto, como não existe tabela de líquido comprimido para , consideraremos como a entalpia do líquido saturado a e como a entalpia do líquido saturado a . Encontramos esses valores na tabela de saturação da água.
Sabendo todas essas informações, podemos iniciar as contas!
Passo 6
Resposta
Exercício Resolvido #8
Claus J. Borgnakke, Gordon J. Van Wylen, Richard E. Sonntag, Fundamentos da Termodinâmica, 6ª ed. São Paulo: Edgard Blücher, 2003, pp. 169-6.87
Um superaquecedor é alimentado com de vapor saturado a e descarrega o vapor a e . O trocador opera em contracorrente e deseja-se que a diferença entre a temperaturade descarga do ar e a de entrada de água seja igual a . Sabendo que a temperatura do ar na seção de alimentação do trocador de calor é , determine a vazão em massa de ar no superaquecedor.
Passo 1
O enunciado pede que a gente calcule a vazão mássica de ar que passa pelo trocador de calor. A figura abaixo mostra todos os dados que o enunciado nos informa para calcular essa vazão .
é a temperatura da água entrando no trocador de calor. é a temperatura do ar entrando no trocador de calor e é a temperatura do ar saindo do trocador de calor. é a pressão da água entrando no trocador de calor e é a pressão da água saindo do trocador de calor. é o título da água entrando no trocador de calor. Ele vale , porque a água que entra no trocador é um vapor saturado!
Agora que sabemos o que cada dado significa, vamos aprender a calcular .
Passo 2
pode ser calculado através da equação de primeira lei para um trocador de calor incluindo duas correntes: uma de ar quente e outra de água. ATENÇÃO! A forma dessa equação não possui o termo de taxa de troca de calor!
onde é a entalpia específica do ar quente entrando no trocador de calor. é a entalpia específica do ar quente saindo do trocador de calor. é a entalpia específica da entrando no trocador de calor. é a entalpia específica da água saindo do trocador de calor.
A fórmula de cima mostra que para calcular precisamos encontrar , , e . Vamos encontar a diferença de entalpias do ar no próximo passo.
Passo 3
O ar pode ser tratado como gás ideal. Por conta disso, pode ser calculado através da fórmula abaixo.
onde é o calor específico do ar a pressão constante e é a temperatura do ar saindo do trocador de calor. vale:
Substituindo essa fórmula na fórmula de , encontramos.
Para calcular precisamos encontrar primeiro . Faremos isso no próximo passo.
Passo 4
Como a água que entra no trocador de calor é um vapor saturado a , encontramos na tabela de saturação da água na mesma linha que a pressão de e na mesma coluna que a temperatura de saturação .
Como a diferença de temperatura entra a água entrando no trocador e a temperatura do ar saindo do trocador é de , podemos descobrir quanto vale .
Convertendo esse valor para kelvin , achamos:
Agora vamos encontrar as entalpias específicas da água e .
Passo 5
Como a água que entra no trocador de calor é um vapor saturado a , encontramos na tabela de saturação da água na mesma linha que a pressão de e na mesma coluna que a entalpia específica do vapor saturado .
Como a água que sai do trocador de calor é um vapor superaquecido a e , encontramos na tabela de vapor superaquecido da água. Esse valor está na mesma linha que a temperatura de e na mesma coluna que a entalpia específica .
Depois de aprender todas essas informações, podemos iniciar as contas!