Exercícios Resolvidos de Teste de Hipóteses para Média Populacional com σ Conhecido
Ver TeoriaEnunciado
Teste de Hipóteses
b) Testar a hipótese se existe diferença entre a média verdadeira das peças da máquina e média verdadeira das peças da máquina , aos níveis de significância de e . Suponha conhecidos os desvios padrões: e . Mostre este resultado através de cálculo e esboce um gráfico da distribuição do teste indicando a área de rejeição e aceitação.
Passo 1
Primeiro vamos anotar de novo os dados de cada amostra...
O exercício pede pra gente testar a hipótese de existir ou não diferença entre as médias verdadeiras das duas máquinas... nosso teste vão ter as seguintes hipóteses:
Concorda? Não importa se um for maior ou menor que o outro, só quero saber se são iguais ou diferentes.
Esse teste é daquele caso
Na real, a gente vai ter que fazer dois testes né, olha que maravilha... um com e outro com de nível de significância.
Passo 2
Já que a gente já montou o teste, vamos fazer a nossa estatística de teste, que nesse caso de diferença entre médias, é:
Substituindo os valores...
Passo 3
Pra fechar a gente precisa saber a região crítica do nosso teste, e ver se estamos fora ou dentro dessa região.
Pra esse teste (caso ), a região crítica é:
Só que vamos ter que fazer duas vezes né, uma pra cada nível de significância pedido...
Passo 4
Pra nível de significância de ...
Usei o mais aproximado, você poderia fazer uma média ponderada dos valores da tabela mais próximos também, daria ... mas a diferença é muito pequena, não altera quase nada na conta.
Nossa região crítica é:
E a nossa estatística de teste deu:
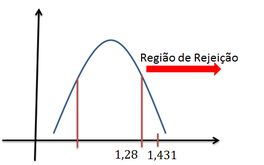
Estamos fora da região crítica (ou de rejeição), então aceitamos ao nível de significância de .
O esboço fica assim:
Passo 5
Pra nível de significância de ...
Usei o mais aproximado de novo.
Nossa região crítica é:
E a nossa estatística de teste deu:
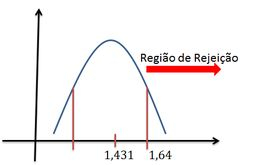
Estamos dentro da região crítica (ou de rejeição), então rejeitamos ao nível de significância de .
O esboço fica assim:
