Sabendo que a estrutura abaixo possui uma temperatura no seu centro de gravidade constante (), Determine o Williot completo da mesma em função dos dados dado na figura. Use como coeficiente de dilatação térmico os comprimentos dados abaixo e para a temperatura do centro de gravidade use . Determine também os deslocamentos e os pontos em que agem.
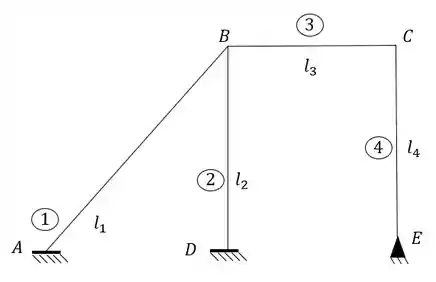
Passo 1
Para fazermos o williot, sabemos que não precisamos determinar hiperestáticos internos ou externos, mas apenas seguir o nosso passo a passo.
Primeiro precisamos determinar os nossos indeslocáveis.
Isso é bem simples, sabemos que no nosso caso os três indeslocáveis, que vão se unir a nossa origem são os pontos A, E e D, dessa maneira teremos que:
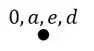
Passo 2
Em seguida devemos determinar o ponto que tenha em comum os pontos já determinados, que no nosso caso é o ponto B, que tem em comum os pontos A e D.
Sabemos que o williot de temperatura possui uma diferença. Primeiro determinamos os pontos que representam os números das barras que chegam em B, e só depois descobrimos de fato o ponto B.
Para determinar esses pontos que representam as barras, devemos traçar na direção de cada barra os deslocamentos que essas barras têm quando são esquentadas, que é dado pela equação e . Fazendo isso teremos que:
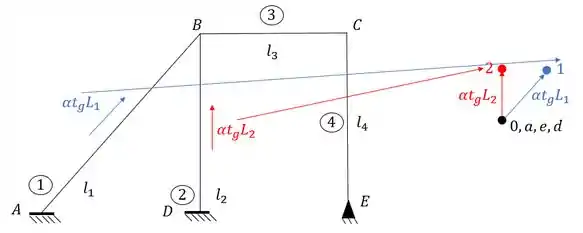
Ou seja, determinamos primeiro os pontos que representam as nossas barras, a partir deles que vamos representar o nosso ponto B.
Tendo os pontos que representam as barras que chegam no ponto B, basta traçarmos perpendiculares as BARRAS, e passarmos elas pelos PONTOS do williot, e assim onde essas retas se encontrarem, será o nosso ponto B. sendo assim teremos que:
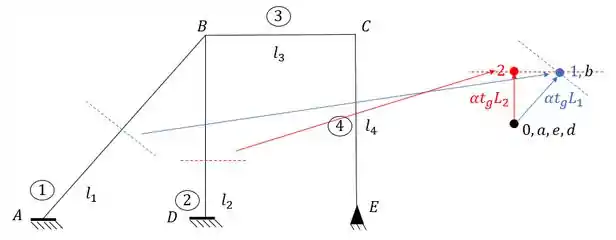
Ligando os pontos teremos que:
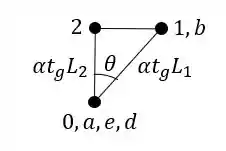
Passo 3
Em seguida devemos determinar o ponto que tenha em comum os pontos já determinados, que no nosso caso é o ponto C, que tem em comum os pontos B e E.
Sabemos que o williot de temperatura possui uma diferença. Primeiro determinamos os pontos que representam os números das barras que chegam em C, e só depois descobrimos de fato o ponto C.
Para determinar esses pontos que representam as barras, devemos traçar na direção de cada barra os deslocamentos que essas barras têm quando são esquentadas, que é dado pela equação e . Fazendo isso teremos que:
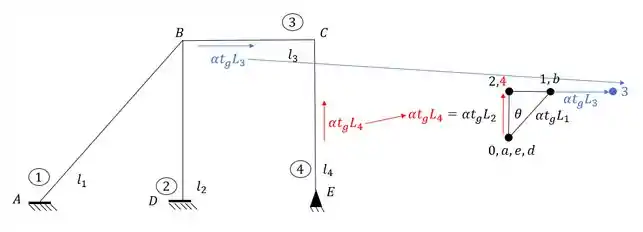
Ou seja, determinamos primeiro os pontos que representam as nossas barras, a partir deles que vamos representar o nosso ponto C.
Tendo os pontos que representam as barras que chegam no ponto C, basta traçarmos perpendiculares as BARRAS, e passarmos elas pelos PONTOS do williot, e assim onde essas retas se encontrarem, será o nosso ponto C. sendo assim teremos que: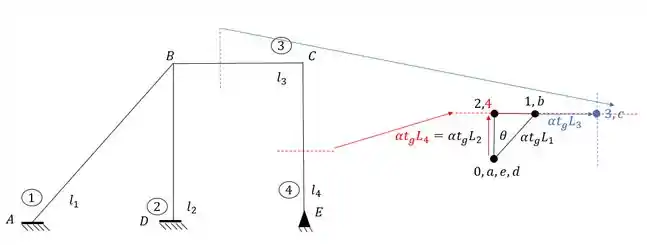
Ligando os pontos teremos que:
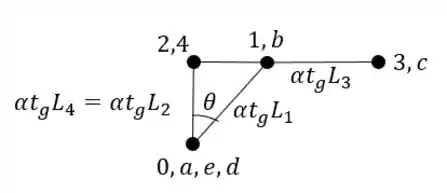
Passo 4
Para determinar a deformação de cada barra precisamos nomear elas, e em seguida achar no williot o seu número, então vamos fazer isso por partes.
Primeiro sabemos que a ordem de determinação dos pontos foi:
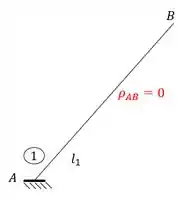
- Barra 1
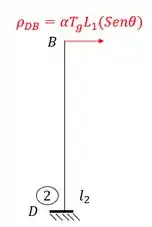
- Barra 2
- Barra 3
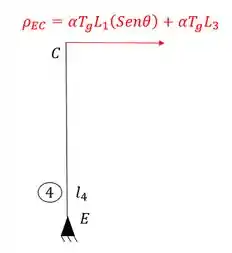
- Barra 4
- Barra 1
- Barra 2
- Barra 3
- Barra 4
Sabendo a ordem podemos definir que o nome da barra 1 é AB. Achando o ponto 1 no nosso williot teremos que.
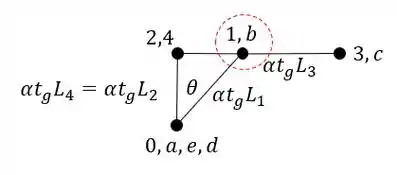
E sabemos que a deformação irá partir do ponto que marcamos para o segundo termo do nome da barra, ou seja, se o nome da barra é AB, o segundo termo será o B. Sendo assim teremos que:
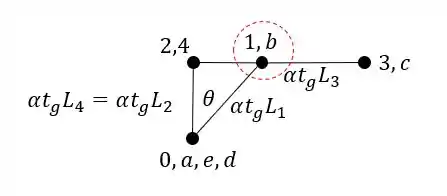
Como o ponto 1 e B estão na mesma posição, teremos que:
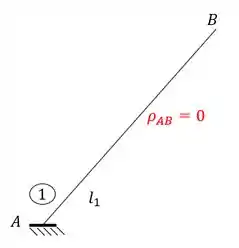
Sabendo a ordem podemos definir que o nome da barra 2 é DB. Achando o ponto 2 no nosso williot teremos que.
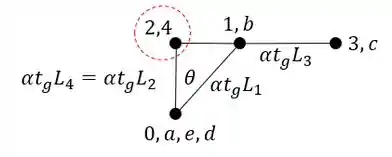
E sabemos que a deformação irá partir do ponto que marcamos para o segundo termo do nome da barra, ou seja, se o nome da barra é DB, o segundo termo será o B. Sendo assim teremos que:

E aplicamos ele no segundo termo do nome da barra, ou seja, no ponto B da barra DB. Sendo assim teremos que:
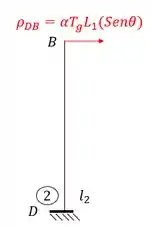
Sabendo a ordem podemos definir que o nome da barra 3 é BC. Achando o ponto 3 no nosso williot teremos que.
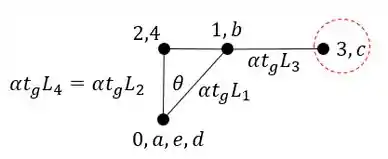
E sabemos que a deformação irá partir do ponto que marcamos para o segundo termo do nome da barra, ou seja, se o nome da barra é BC, o segundo termo será o C. Sendo assim teremos que:
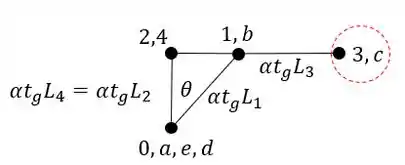
Como os pontos 3 e C estão na mesma posição, teremos que.
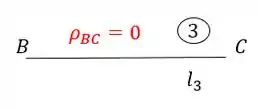
Sabendo a ordem podemos definir que o nome da barra 4 é EC. Achando o ponto 4 no nosso williot teremos que.
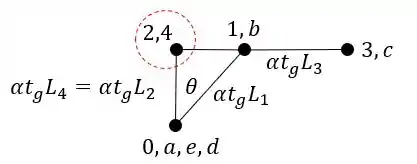
E sabemos que a deformação irá partir do ponto que marcamos para o segundo termo do nome da barra, ou seja, se o nome da barra é EC, o segundo termo será o C. Sendo assim teremos que:
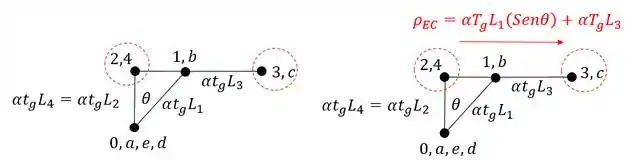
E aplicamos ele no segundo termo do nome da barra, ou seja, no ponto C da barra DC. Sendo assim teremos que:
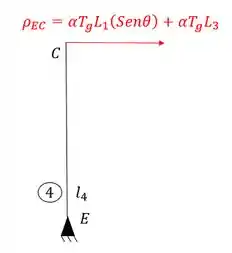
Resposta
Williot
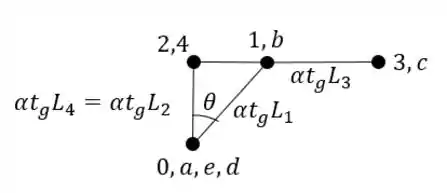
Deformações e ponto de aplicação:
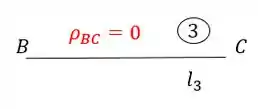
Resposta
Ei, a resposta está no passo a passo :)