Dadas as funções:
Encontre uma função que dependa apenas das variáveis .
Passo 1
O exercício aqui entrega duas funções e pede para você encontrar a função composta.
A ideia de funções compostas é altamente importante independente da área, por exemplo na programação gostamos de dividir essas funções dessa forma pois gera um código mais organizado, imagine só você colocar a função dentro da função e sair resolvendo as operações, bem complicado né?

Então, estamos aqui para te ensinar uma forma mais prática, preparado? vamos láá
A ideia aqui é pegar a função e substituí-lo dentro da função .
Para te mostrar que se você gera uma função e na linha seguinte essa função vira uma variável da , o Matlab entende que o resultado da precisa ser jogado como entrada na função .
Então vamos fazer utilizando as variáveis simbólicas pois não temos os valores das variáveis e além disso, queremos encontrar uma expressão no final de tudo e não um valor numérico. Quando acontecer essas duas coisas, você já tem que se lembrar das variáveis simbólicas!
Sendo assim o passo a passo é o seguinte:
1-Introdução das variáveis simbólicas.
2- Implementação da função
3- Implementação da função
Passo 2
Agora que criamos o passo a passo vamos apenas implementar as variáveis no Matlab.
Primeiramente vamos implementar as variáveis simbólicas do código, para isso temos:
Uma vez que criamos as variáveis simbólicas vamos criar a função
Agora vamos implementar a função
Passo 3
Se digitou tudo certinho no seu Matlab deve aparecer algo mais ou menos assim:
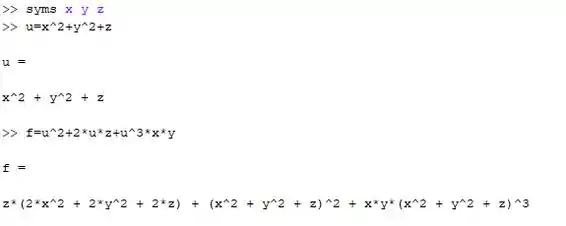
Resposta
