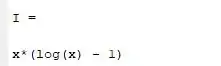Na teoria do cálculo diferencial e integral aprendemos que certas integrais são bem complicadas de resolver, uma delas é a seguinte integral:
Através de técnicas desenvolvidas na disciplina nos é mostrado que essa integral gera a seguinte primitiva:
Utilize a função para comprovar que o Matlab realmente consegue calcular essas integrais.
Dica: a sintaxe da função int é a seguinte , e para o command window a função é escrita como l
Passo 1
Essa questão é uma aplicação de variável simbólica, uma ideia intuitiva para deduzir isso é que não temos valores nenhum das variáveis
Mas o correto pare se pensar é que estamos atrás de uma expressão final, uma função propriamente dita e o Matlab só consegue imprimir funções quando trabalhamos com variáveis simbólicas.
A ideia aqui é pegar a função e integrar utilizando a função int. A função int é uma função do Matlab que é utilizada para o cálculo de integrais simbólicas.
Sendo assim, o passo a passo para resolução do exercício é o seguinte:
1-Introdução das variáveis simbólicas, que no caso é a variável X.
2- Implementação da função
3- Implementação da função
4-Comparar com o resultado fornecido e verificar se realmente apresentam os mesmos resultados.
Passo 2
Agora que criamos o passo a passo, vamos apenas implementar as variáveis no Matlab.
Primeiramente vamos começar pela parte mais importante que é implementar as variáveis simbólicas do código. Como podemos ver, o logaritmo depende apenas de um único parâmetro que é o X. Sendo assim, a variável independente vai ser nossa variável simbólica.
Então, a variável simbólica é:
Uma vez que criamos as variáveis simbólicas vamos criar a função
Agora vamos implementar a função
Passo 3
Se digitou tudo certinho no seu Matlab deve aparecer algo mais ou menos assim:

Executando o programa deverá aparecer na sua janela de command window a seguinte informação:

Olhando a uma primeira visão não parece a mesma coisa né?
Mas, realizando as distributivas temos que:
Tem uma diferença da integral analítica que é dada pela soma de uma constante que é a constante de integração.
Resposta