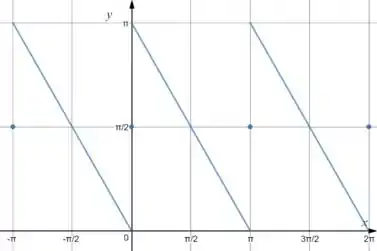
Seja dada por
- Encontre uma série de Fourier desta função com período ;
- Esboce o gráfico da série de Fourier no intervalo
Passo 1
Precisamos agora encontrar a Série complexa de Fourier de , a fórmula é:
E a fórmula do coeficiente é:
Assim, precisamos calcular os coeficientes para encontrarmos a série, então:
Fazendo a substituição:
Resolvendo a integral:
Vamos agora calcular . Assim:
Com isso, temos que nossa série de Fourier ficou:
Passo 2
Agora é só repetir no intervalo e usar o teorema da convergência da série de Fourier que chegamos no seguinte:
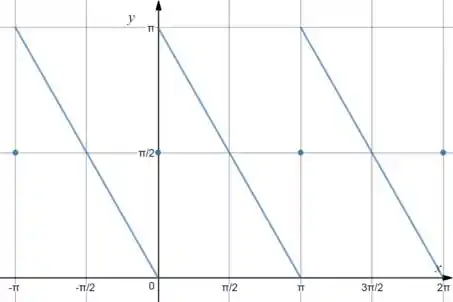
Resposta