Considere a situação em que se deseja utilizar, para a homogeneização de um determinado biodiesel , um tanque de agitação que apresenta as seguintes características:
Estime o valor da potência consumida pelo sistema de agitação, assumindo que o tanque apresenta turbina de seis pás retas e:
- Quatro chicanas
- Sem chicanas
Passo 1
O enunciado já deu as dimensões do sistema de agitação e a quantidade de rotações do impelidor, . Daí para achar a potência, , usamos:
Como quase todos os dados fornecidos já estão no sistema de unidades CGS, é com ele que vou trabalhar. Por isso, vou converter essa rotação em rpm para o CGS, isto é, preciso de “por segundo” e não de “por minuto”:
Tanto no item a como no item b, os valores de (depende do fluido), (é dito constante) e (o tanque é o mesmo) se mantém iguais. Então posso substituir os valores e:
E como estamos trabalhando no CGS, isso está em .
Já o valor do depende do Reynolds e da configuração de cada tanque agitado. O Reynolds é calculado por:
Sendo que
O é dado como ; como a unidade padrão do CGS é St (Stokes):
Daí:
A partir do Reynolds, achamos o valor de pelo gráfico:
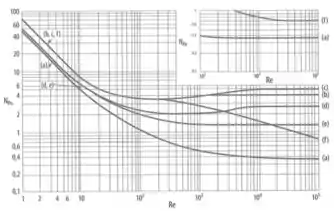
Como depende da configuração do tanque, vamos ter que ver isoladamente pra cada caso.
Passo 2
- Quatro chicanas
- Sem chicanas
O primeiro item pede a potência quando o tanque tem quatro chicanas (que é o “padrão”, como vimos na teoria. Como foi dito que o tanque apresenta pás retas, usamos a (b) do gráfico.
Olhando no gráfico a curva (b) para :
Daí:
Passo 3
Temos que fazer a mesma coisa do passo anterior, mas agora o tanque não tem chicanas então usamos a curva (f).
Olhando no gráfico a curva (f) para :
Daí: