Deseja-se avaliar um sistema de agitação destinado à oxidação de matéria orgânica de um efluente que apresenta massa específica igual a e viscosidade dinâmica igual a . Conhecendo-se a capacidade de descarga do impelidor, que é igual a , e a vazão requerida de ar igual a , pede-se:
b) Obtenha o valor da potência útil de agitação referente ao sistema projetado. Verifique também o nível de agitação.
Dados do tanque agitado:
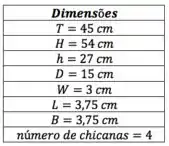
Passo 1
Para calcular a potência útil, vamos ter que usar:
Mas repara que NÃO temos o valor de e nem de :/ Bora procurar um jeito de resolver a questão então.
A gente tem a capacidade de descarga do impelidor:
E podemos escrever em função do número de bombeamento, :
Mas essa expressão também tem o , que não conhecemos...
Tem uma outra expressão que envolve o , que é o número de Reynolds do impelidor:
Embora a gente também não conheça o Reynolds (e nem tenha como determiná-lo de cara), a gente sabe que ele está relacionado tanto com o como com o . Os relacionamos pelos gráficos que vimos lá na teoria.
Para :
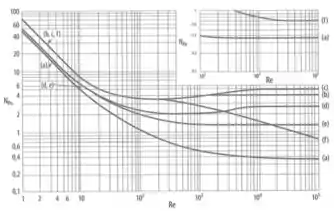
Para :
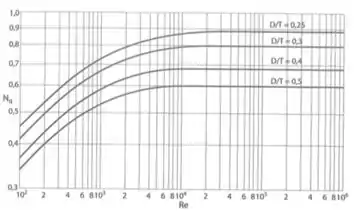
Sendo este gráfico apenas para impelidor do tipo turbinas de pás inclinadas a e com chicanas no tanque, que é o caso do problema.
O lance vai ser ficar iterando: chutar um valor de , calcular o Reynolds pra esse , daí calcular (pelo primeiro gráfico). Daí vamos “poder” calcular por:
Além disso, usamos esses mesmos e para achar um .
é dado como . O que vamos fazer é usar a equação:
E isolar o :
Nós vamos usar esse calculado para recalcular o . Daí usamos esse novo para repetir os cálculos. E vamos ficar repetindo isso até o valor de convergir, isto é, ficar constante. Aí teremos o valor de .
Passo 2
Antes de começar as iterações, vou já colocar o máximo de números possível no problema pra ficar com menos letras haha Começando com o Reynolds:
E aquela expressão do isolado:
Ah, outro detalhe é que vamos precisar de para obter o valor de do gráfico.
Repara que estou usando o CGS.
Vou organizar as iterações numa tabela. O primeiro chute vai ser .
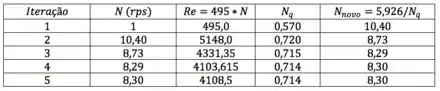
Um resumo dos resultados:
Passo 3
Agora que temos o Reynolds, podemos calcular o pra um sistema SEM borbulhamento pelo gráfico:
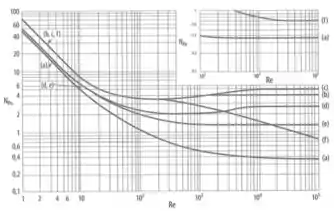
Usando o e a curva (e) (que vai ser uma aproximação já que não é exatamente ):
Ainda falta um detalhe: o nosso sistema é sim borbulhado então temos que corrigir o número de potência. Fazemos isso com aquele outro gráfico que vimos na teoria:
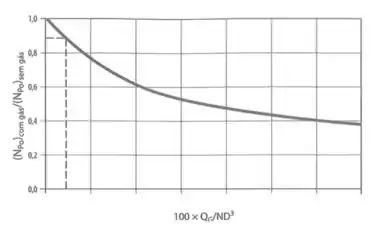
O valor no eixo x é:
Pelo gráfico:
Daí:
Passo 4
Finalmente podemos calcular o que a questão pede, :
Já o nível de agitação tem fórmula:
Não chegamos a calcular o , mas temos e sabemos que . Daí:
Usando em :