Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Autovalor e Autovetor

Ver Todos os Exercícios

Teoria

Fala aí! Bem vindo ao Responde Aí. Hoje a gente vai aprender juntinhos o que é Autovalor e Autovetor!

O que são Autovalores e Autovetores?

Vamos direto ao que interessa! Temos a seguinte definição formal de autovalores e autovetores:

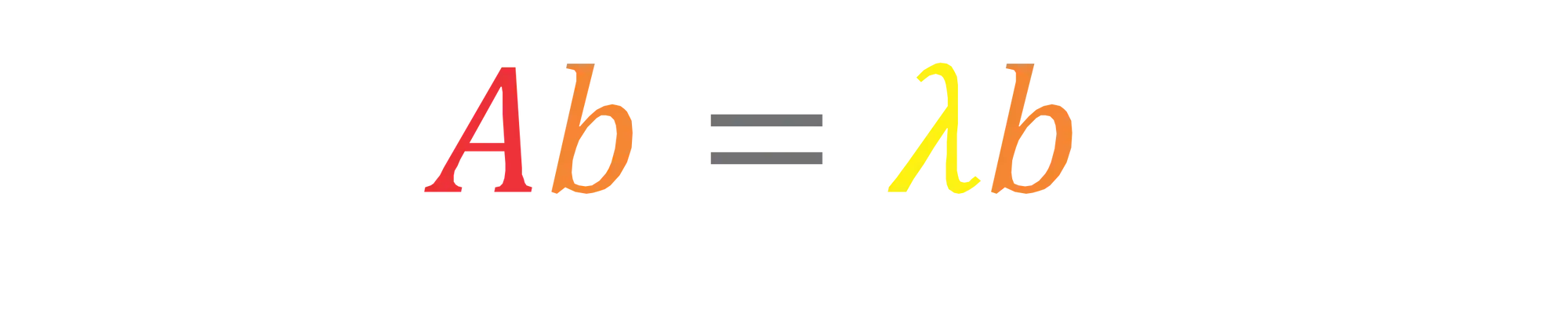
Seja uma matriz quadrada. Um vetor não nulo é autovetor associado ao Autovalores e autovetores se:

Autovalores e Autovetores
Autovalores e Autovetores

Esse é uma matriz quadrada não nula, é um vetor genérico que será nosso autovetor e será o autovalor! Se liga nesse exemplo pra ficar mais claro:

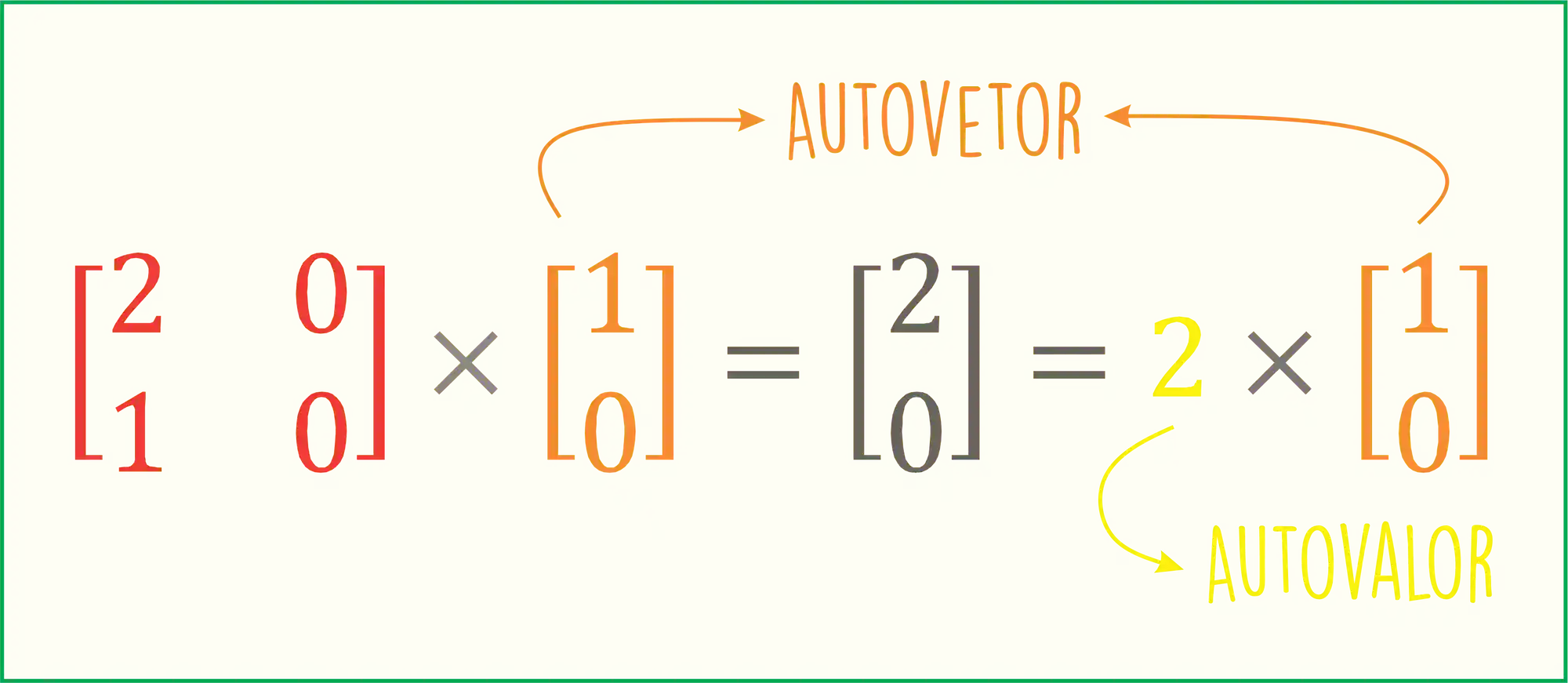
Autovalor e autovetor: Exemplo
Autovalor e autovetor: Exemplo

Temos a matriz quadrada de vermelhinho ali em cima e quando multiplicamos ela pelo autovetor temos como resultado o próprio autovetor multiplicada pelo autovalor .

Ou seja, os autovetores são vetores que após aplicados a matriz aparecem no resultado multiplicados um autovalor . Ou seja, a matriz sofreu uma transformação mas os vetores continuaram aparecendo no resultado! Na prática a gente tem que estar sempre ligado nas seguintes considerações:

  • A matriz TEM que ser quadrada;
  • Os autovalores e autovetores estarão sempre juntos;
  • Cada autovetor só pode estar associado a um autovalor ;
  • Autovalores podem estar associados a mais de um autovetor ;
  • pode ser zero, mas não.

📢 Clique para ver mais:

Quer saber mais sobre autovalores e autovetores? Se liga nesse vídeo completaço que o Responde Aí preparou pra você e aprenda como achar os autovalores e autovetores! 👇

Como achar o Autovetor de uma matriz?

Vamos considerar a seguinte matriz:

Vamos descobrir os autovalores e autovetores dessa matriz! Para fazer isso vamos ter que calcular as raízes do polinômio característico, que é a seguinte expressão:

Para encontrarmos os autovalores e vamos calcular as raízes do polinômio característico fazendo, :

Primeiro calculando o determinante:

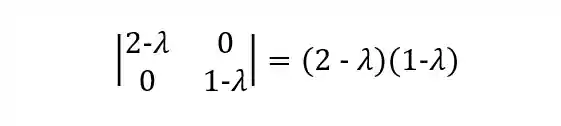
Cálculo do determinante
Cálculo do determinante

E igualando a zero:

Encontramos e , show já temos os autovalores. Agora vamos descobrir os autovetores associados a cada um desses autovalores. Podemos fazer isso com duas equações:

Para vamos fazer:

Logo, pensando como um vetor genérico :

Calculando essa multiplicação de matrizes, encontramos o seguinte sistema:

Como queremos um vetor , os autovetores associados ao autovalor tem a forma:

Para o autovalor vamos usar:

Dessa forma:

Resolvendo o sistema, encontramos e , e por isso queremos vetores com a carinha , logo os autovetores associados ao autovalor tem a forma:

Exemplo: A matriz tem três autovalores distintos, , e . Os vetores e são autovetores associados a e respectivamente. Assinale abaixo o vetor que poderia ser um autovetor associado a

a)

b)

c)

d)

A resolução desse problema, você pode conferir no vídeo abaixo!

Vamos praticar com exercícios?!

Exemplo: A matriz tem três autovalores distintos, , e . Os vetores e são autovetores associados a e respectivamente. Assinale abaixo o vetor que poderia ser um autovetor associado a

Exercícios Resolvidos

Exercício Resolvido #1

Marco Cabral e Paulo Goldfeld, Curso de Álgebra Linear Fundamentos e Aplicações, 3ª Ed., Rio de Janeiro, Instituto de Matemática, 2012, pp. 209 – Prob 7.2

Em cada item determine se v → é autovetor de A .

a   v → = 1 4 e A = - 1 1 - 1 8

b   v → = 4 - 3 1 e A = 3 7 9 - 4 - 5 1 2 4 4

Passo 1

Para saber se é autovetor, é só ver se A ∙ v → é múltiplo do vetor v → .

Na letra ( a ) :

A ∙ v → = - 1 1 - 1 8 ∙ 1 4 = 3 31

Como ( 3 ,   31 ) não é múltiplo de ( 1 ,   4 ) , então v → não é autovetor de A .

Passo 2

Agora é só fazer a mesma coisa na letra ( b ) .

A ∙ v → = 3 7 9 - 4 - 5 1 2 4 4 ∙ 4 - 3 1 = 12 - 21 + 9 - 16 + 15 + 1 8 - 12 + 4 = 0 0 0

De fato, ( 0 ,   0 ,   0 ) é múltiplo de ( 4 ,   - 3 ,   1 ) , e o autovalor é 0 .

Por isso ( 4 ,   - 3 ,   1 ) é autovetor de A .

Resposta

a   Não.

b   Sim.

Exercício Resolvido #2

UFRJ, Álgebra Linear, P2 – 2016.1, Questão 03

Seja A = 2 0 1 0 1 0 - 2 0 5 e seja v → = v 1 , v 2 , v 3 um autovetor de A associado ao autovalor 4 . Se v 1 = 1 , quanto vale v 3 ?

a   2

b   3

c   4

d   5

Passo 1

Se v é um autovetor associado ao autovalor 4 , então:

2 0 1 0 1 0 - 2 0 5 v 1 v 2 v 3 = 4 v 1 4 v 2 4 v 3

Mas sabemos que v 1 = 1 , então:

2 0 1 0 1 0 - 2 0 5 1 v 2 v 3 = 4 4 v 2 4 v 3

Passando isso para a forma de sistema:

2 + v 3 = 4 v 2 = 4 v 2 - 2 + 5 v 3 = 4 v 3

Po, dá pra matar a questão só olhando a primeira equação! Por ela temos que:

2 + v 3 = 4 ⇒ v 3 = 2

Resposta

Letra ( a )

Exercício Resolvido #3

UFRJ, Álgebra Linear, P4 – 2015.1, Questão 09

Seja A uma matriz 3 × 3 , não-nula, tal que a terceira coluna é igual a soma das duas primeiras. Assinale abaixo um autovetor de A :

a   1 , - 1,1 T

b   1,1 , - 1 T

c   1,1 , 2 T

d   1,1 , - 2 T

Passo 1

Vamos escrever a matriz do enunciado:

A = a d a + d b e b + e c f c + f

Podemos calcular os autovalores e depois os autovetores da matriz, mas isso daria um bocado de trabalho.

Como somamos duas colunas para formar a terceira coluna essa matriz ela será LD (Linearmente Dependente), pois um vetor coluna é combinação linear dos outros dois.

Bom, e o que isso quer dizer? Quer dizer um monte de coisas, mas o que nos interessa é que a dimensão do seu núcleo é maior que 1 . Isso quer dizer que ela possui o autovalor 0 !

Desse modo, sabemos que os autovetores ( x ) tem que obedecer a seguinte equação:

A x = 0

Podemos então testar os autovetores das alternativas para ver qual das opções é solução para a equação acima. Beleza?!

Passo 2

Item (a)

a d a + d b e b + e c f c + f ∙ 1 - 1 1 = 2 a 2 b 2 c ≠ 0

Passo 3

Item (b)

Fazendo as continhas, temos

a d a + d b e b + e c f c + f 1 1 - 1 = 0 0 0

Passo 4

Item (c)

a d a + d b e b + e c f c + f 1 1 2 = 3 a + 3 d 3 b + 3 e 3 c + 3 f ≠ 0

Passo 5

Item (d)

a d a + d b e b + e c f c + f 1 1 - 2 = - a - d - b - e - c - f ≠ 0

Fim de papo, é a letra b . Show de bola?!

Resposta

Letra ( b )

Exercício Resolvido #4

UFRJ, Álgebra Linear, P3 – 2014.2, Questão 01

A matriz A 3 × 3 tem três autovalores distintos, λ 1 , λ 2 e λ 3 . Os vetores v = 1,1 , 0 e u = 0,1 , 1 são autovetores associados a λ 1 e λ 2 respectivamente. Assinale abaixo o vetor que poderia ser um autovetor associado a λ 3 :

( a ) - 1,0 , 1

( b ) 2,1 , - 1

( c ) 2,3 , 1

( d ) 1 , - 2,1

Passo 1

O que você precisa lembrar pra resolver essa questão é que o mesmo autoespaço não pode estar associado à dois ou mais autovalores distintos! Sendo assim, como λ 1 , λ 2 e λ 3 são autovalores distintos, então o autovetor associado a λ 3 deve ser L I (Linearmente Independentes) em relação à 1,1 , 0 e 0,1 , 1 !

Para checar se os vetores são LI podemos montar uma matriz onde as duas primeiras linhas são os autovetores dados, e a terceira linha o vetor que queremos checar se é LI com os demais. Se conseguirmos zerar a matriz ele será LD, caso contrário, será LI.

Vamos começar pela letra (a), teremos a matriz:

1 1 0 0 1 1 - 1 0 1

Vamos fazer manipular a matriz com as operações elementares, por exemplo:

1 1 0 0 1 1 - 1 0 1 L 3 ← L 3 + L 1   1 1 0 0 1 1 0 1 1 L 3 ← L 3 - L 2 1 1 0 0 1 1 0 0 0

Conseguimos zerar a linha, logo são vetores LD e podemos eliminar a letra (a). Beleza?!

Passo 2

Letra (b)

Montando a matriz:

1 1 0 0 1 1 2 1 - 1

Manipulando a matriz:

1 1 0 0 1 1 2 1 - 1 L 3 ← L 2 - 2 L 1 1 1 0 0 1 1 0 - 1 - 1 L 3 ← L 3 + L 2 1 1 0 0 1 1 0 0 0

Conseguimos zerar a linha, logo são vetores LD e podemos eliminar a letra (b).

Passo 3

Letra (c)

Montando a matriz:

1 1 0 0 1 1 2 3 1

Manipulando a matriz:

1 1 0 0 1 1 2 3 1 L 3 ← L 3 - 2 L 1 1 1 0 0 1 1 0 1 1 L 3 ← L 3 - L 2 1 1 0 0 1 1 0 0 0

Conseguimos zerar a linha, logo são vetores LD e podemos eliminar a letra (c)

Passo 4

Só sobrou a letra (d) , então com certeza é a resposta certa, mas vamos ver o que acontece quando tentamos zerar a matriz.

Montando a matriz:

1 1 0 0 1 1 1 - 2 1

Manipulando a matriz:

1 1 0 0 1 1 1 - 2 1 L 3 ← L 3 - L 1 1 1 0 0 1 1 1 - 3 1 L 3 ← L 3 + 3 L 2 1 1 0 0 1 1 0 0 4

Não conseguimos zerar a última linha, logo, ele é o único L I com relação aos demais, e portanto é o que pode ser um autovetor associado a λ 3 .

Show de bola?!

Resposta

Letra ( d )

Exercícios de Livros Relacionados

Encontre d e t ( A ) , sabendo que A tem polinômio característico p ( λ ) . p λ = λ 4 - λ 3 - 7
Encontre d e t ( A ) , sabendo que A tem polinômio característico p ( λ ) . p λ = λ 3 - 2 λ 2 + λ + 5
No Exercício 11, encontre uma decomposição em valores singulares de A. A = 1 0 1 1 - 1 1
No Exercício 10, encontre uma decomposição em valores singulares de A. A = - 2 - 1 2 2 1 - 2
No Exercício 12, encontre uma decomposição em valores singulares de A. A = 6 4 0 0 4 0