Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Coordenadas Esféricas

Ver Todos os Exercícios

Teoria

Fala aí! Seja bem vindo ao Responde Aí! Bora aprender sobre Coordenadas Esféricas?

O que são Coordenadas Esféricas?

O Sistema de Coordenadas Esféricas é uma um sistema de referencial usado pra escrever a localização em um espaço esférico. Nele, um ponto qualquer é representado pelas coordenadas e .

-Hãam?! 😖

Bora aprender isso na prática! Imagina que Pedrinho esta em cima de uma esfera gigante e a gente quer saber exatamente sua localização.

Pedrinho na esfera
Pedrinho na esfera

Concorda comigo que as coordenadas retangulares não conseguem expressar de uma forma muito legal a posição do Pedrinho? Pra isso vamos usar as coordenadas esféricas!

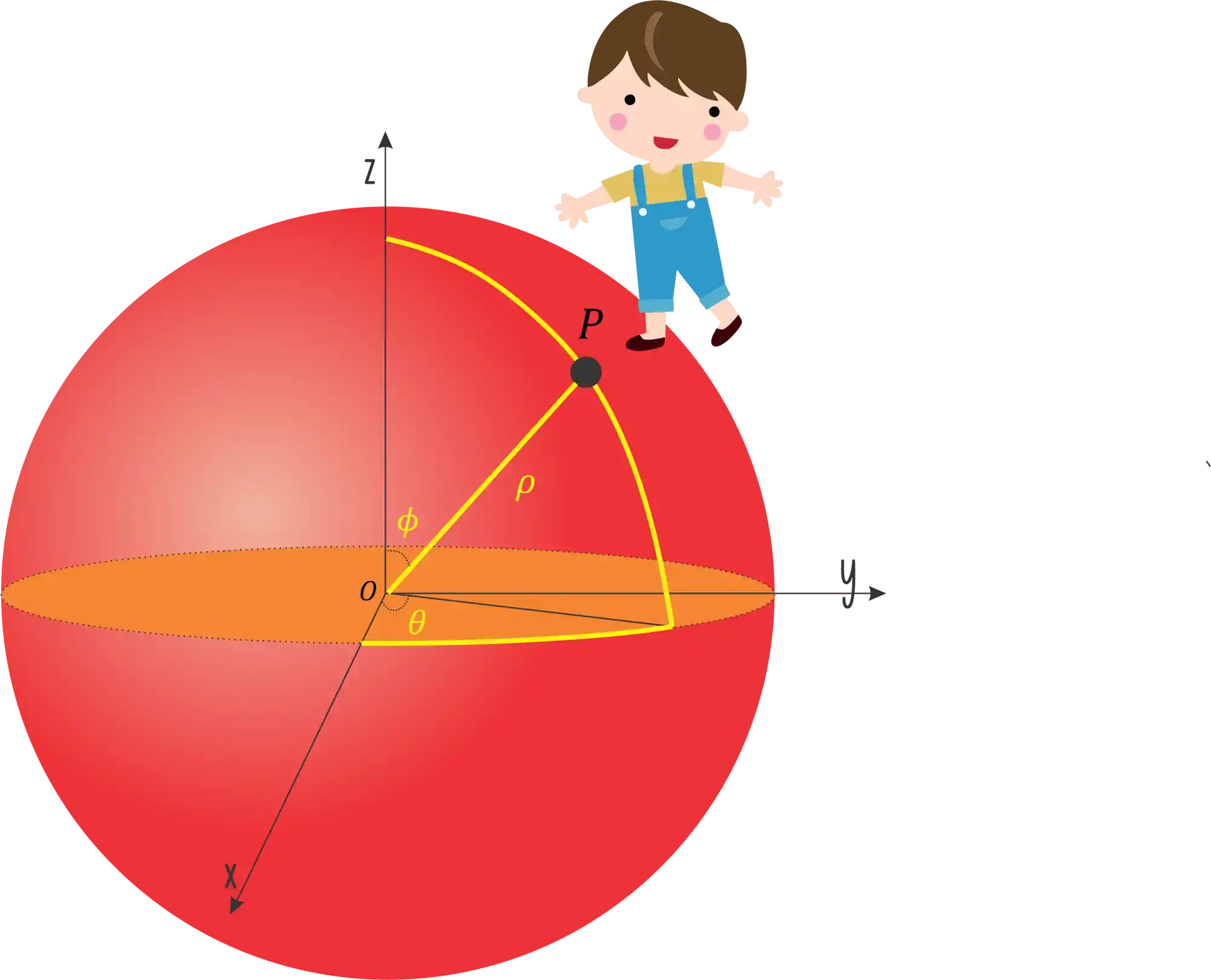
Coordenadas Esféricas: Posição
Coordenadas Esféricas: Posição

Nas coordenadas esféricas a gente pode escrever a posição de Pedrinho usando:

  • é o ângulo entre os eixos e
  • é a a distância do ponto até a origem .
  • é o ângulo entre o vetor  e o eixo .

📢 Clique para saber mais:

Como usar as Coordenadas Esféricas

Beleza, mas e na prática…nos exercícios. Como a gente usa as coordenadas esféricas?!

Pra responder essa pergunta, se liga nesse vídeo super completo que o Responde Aí preparou pra você sobre Coordenadas Esféricas! Nele a gente fala um pouco mais sobre como usar essas coordenadas, como converter pra coordenadas cartesianas e muito mais!

Coordenadas Esféricas para Coordenadas Cartesianas

Em alguns momentos as coordenadas cartesianas são mais práticas de se trabalhar. Para converter as coordenadas esféricas em cartesianas a gente precisa relacionar as coordenadas e com as coordenadas e .

Considere o seguinte ponto :

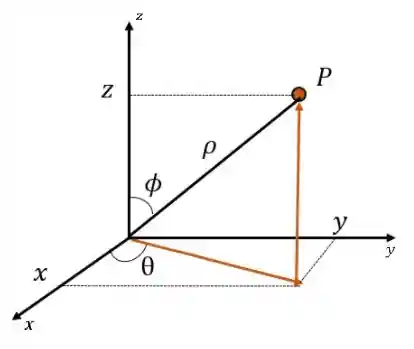
Ponto P.
Ponto P.

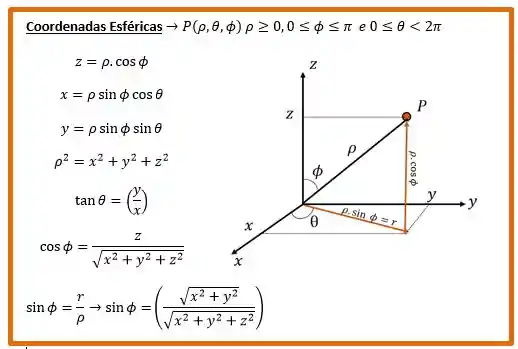
Podemos escrever as seguintes relações entre as coordenadas esféricas e retangulares:

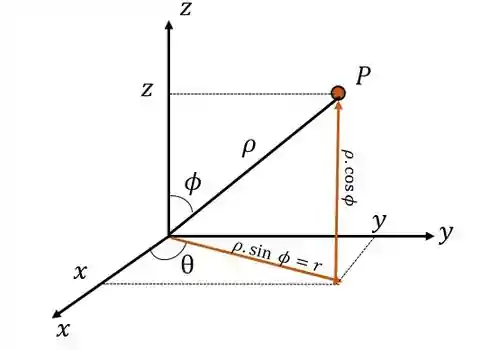
Relações trigonométricas entre as coordenadas esféricas e cartesianas
Relações trigonométricas entre as coordenadas esféricas e cartesianas

Então ficamos com:

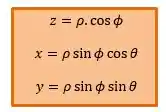
Coordenadas Esféricas para Coordenadas Cartesianas
Coordenadas Esféricas para Coordenadas Cartesianas

Coordenadas Esféricas: Resumo

Agora pra a gente encerrar esse tópico com chave de ouro, se liga nesse resumo sobre coordenadas esféricas que a gente preparou pra você!

Coordenadas Esféricas: Resumo
Coordenadas Esféricas: Resumo

Agora vamos praticar com exercícios!

Coordenadas Esféricas para Coordenadas Cartesianas

Coordenadas Esféricas: Resumo

Exercícios Resolvidos

Exercício Resolvido #1

Unicamp, Lista 3 – Geometria Analítica (MA141), 2014, pág 1, ex. 12

Encontre uma equação em coordenadas cartesianas da superfície cuja equação em coordenadas esféricas é dada:

  1. ρ = 3 tan  ⁡ θ

  2. ρ = 9 sec ⁡ ϕ

Passo 1

Nesse exercício nós temos as expressões em coordenadas esféricas e queremos passar para coordenadas cartesianas. Sempre, fique atento em qual coordenada a equação está e para qual devemos passar para não confundir e fazer errado! Blz?

Então, bora passar para as coordenadas cartesianas!!

Passo 2

  1. Temos a seguinte expressão ρ = 3 tan  ⁡ θ Como queremos passar para as coordenadas cartesianas usaremos as seguintes relações:

    2. ρ 2 = x 2 + y 2 + z 2 →   ρ = x 2 + y 2 + z 2       ( 1 )

    tan ⁡ θ = y x     ( 2 )

    cos ⁡ ϕ = z x 2 + y 2 + z 2   ( 3 )

    Substituindo as relações 1 ,   ( 2 ) e ( 3 ) na expressão ρ = 3 tan  ⁡ θ , teremos:

    ρ = 3 tan  ⁡ θ

    x 2 + y 2 + z 2 = 3 y x

    Elevando os dois lados ao quadrado e rearrumando, teremos:

    x 2 x 2 + y 2 + z 2 - 9 y 2 = 0

    Passo 3

  2. ρ = 9 sec ⁡ ϕ

Utilizando as mesmas relações 1 ,   ( 2 ) e ( 3 ) , temos:

ρ = 9 sec ⁡ ϕ = 9 cos ⁡ ϕ

x 2 + y 2 + z 2 = 9 x 2 + y 2 + z 2 z

Aqui a vontade de cortar a raíz dessa coisa monstruosa é grande, mas cuidado!

Não podemos fazer isso, porque não necessariamente o número dentro dessa raíz é diferente de zero, beleza??

Então passando o z pro outro lado multiplicando:

z x 2 + y 2 + z 2 = 9 x 2 + y 2 + z 2

Agora passando tudo pro lado esquerdo:

z x 2 + y 2 + z 2 - 9 x 2 + y 2 + z 2 = 0

Colocando a raíz em evidência, vamos ter:

z - 9 x 2 + y 2 + z 2 = 0

Elevando os dois lados ao quadrado:

z - 9 2 ( x 2 + y 2 + z 2 ) = 0

Chegamos em mais uma expressão!!

Resposta

a )   x 2 x 2 + y 2 + z 2 - 9 y 2 = 0

b )   z - 9 2 ( x 2 + y 2 + z 2 ) = 0

Exercício Resolvido #2

Elaboração Própria

Encontre uma equação em coordenadas esféricas para:

  1. x 2 + y 2 = z
  2. 3 x + 2 y + 6 z = 0

Passo 1

Temos as expressões em coordenadas cartesianas (nossa velha conhecida haha) e queremos passar as expressões para a nossa mais nova conhecida, coordenadas esféricas!! Hehe

Para isso, vamos utilizar as seguintes relações:

z = ρ . cos ⁡ ϕ     ( 1 )

x = ρ sin ⁡ ϕ cos ⁡ θ       ( 2 )

y = ρ sin ⁡ ϕ sin ⁡ θ       ( 3 )

Passo 2

  1. x 2 + y 2 = z

    2. Urilizando as relações 1 ,   ( 2 ) e ( 3 ) temos:

    x 2 + y 2 = z → ( ρ sin ⁡ ϕ cos ⁡ θ ) 2 + ( ρ sin ⁡ ϕ sin ⁡ θ ) 2 = ρ . cos ⁡ ϕ

    Rearranjando:

    ρ sin ⁡ ϕ 2 ( cos ⁡ θ ) 2 + ( sin ⁡ ⁡ θ ) 2 = ρ . cos ⁡ ϕ

    ρ sin ⁡ ϕ 2 =   ρ . cos ⁡ ϕ

    ρ ( ρ sin 2 ⁡ ϕ - cos ⁡ ϕ ) = 0

    Chegamos na nossa expressão!!

    ρ ( ρ sin 2 ⁡ ϕ - cos ⁡ ϕ ) = 0

    Passo 3

  2. 3 x + 2 y + 6 z = 0

O mesmo passo a passo do item anterior, substituindo, teremos:

3 x + 2 y + 6 z = 0 → 3 ρ sin ⁡ ϕ cos ⁡ θ + 2 ρ sin ⁡ ϕ sin ⁡ θ + 6 ρ . cos ⁡ ϕ = 0

Rearranjando a expressão:

ρ sin ⁡ ϕ ( 3 cos ⁡ θ + 2 sin ⁡ θ ) + 6 ρ . cos ⁡ ϕ = 0

Acabouuu!! Você tirou de letra!! ;)

Resposta

a )   ρ ( ρ sin 2 ⁡ ϕ - cos ⁡ ϕ ) = 0

b )   ρ sin ⁡ ϕ ( 3 cos ⁡ θ + 2 sin ⁡ θ ) + 6 ρ . cos ⁡ ϕ = 0

Exercício Resolvido #3

Elaboração Própria

Identificar a superfície cuja equação em coordenadas esféricas é ρ = 2 a cos ⁡ ϕ   ( a > 0   c t e ) .

Passo 1

Esse exercício é um pouco diferente dos outros que já fizemos!! Antes, tínhamos uma expressão e queríamos passar a expressão para outro sistema de coordenadas. Agora, temos uma expressão em coordenadas esféricas e queremos identificar a superfície. Mas, para isso, vamos passar a expressão para as coordenadas cartesianas para ficar mais fácil identificar a superfície. Bora identificar a superfície?

Passo 2

Primeiro, vamos passar a expressão ρ = 2 a cos ⁡ ϕ que está em coordenadas esféricas para as coordenadas cartesianas. Para isso, vamos utilizar as seguintes relações:

ρ 2 = x 2 + y 2 + z 2 →   ρ = x 2 + y 2 + z 2

cos ⁡ ϕ = z x 2 + y 2 + z 2  

Substituindo:

ρ = 2 a cos ⁡ ϕ →   x 2 + y 2 + z 2 = 2 a z x 2 + y 2 + z 2  

x 2 + y 2 + z 2 = 2 a z

x 2 + y 2 + ( z - a ) 2 = a 2

Essa superfície é uma esfera de centro ( 0 ,   0 ,   a ) e raio a .

Pronto!! Viu como ficou mais fácil identificar a superfície passando para as coordenadas cartesianas!! ;)

Resposta

E s f e r a   d e   c e n t r o   0 ,   0 ,   a e   r a i o   a

Exercício Resolvido #4

Lista Unicamp – Geometria Analítica (MA141), pág 1, ex. 1640 - Adaptado

As coordenadas esféricas estão relacionadas com as coordenadas em longitude e latitude usadas na navegação. Para ver como, vamos definir um sistema de coordenadas retangulares (ou cartesianas) com sua origem no centro da Terra, o seu eixo zz  positivo passando pelo Pólo Norte e o seu eixo xx positivo passando pelo meridiano principal. Supondo a Terra uma esfera de raio  ρ = 4000 ρ = 4000   m i l h a s , então cada ponto sobre a Terra tem coordenadas esféricas da forma ( 4000 ,   θ ,   ϕ ) ( 4000 ,   θ ,   ϕ ) , onde ϕ ϕ  e  θ θ determinam a latitude e a longitude do ponto. É comum especificar longitudes em graus leste ou oeste do meridiano principal e latitudes em graus norte ou sul do Equador. A cidade de New Orleans, nos EUA, está localizada a  90 ° 90 °  de longitude oeste e  30 ° 30 °  de latitude norte. Determine as coordenadas retangulares associadas a esta localização (suponha que a distância esteja em milhas).

Passo 1

Parece complicado, mas é de boinhas! Vamos por partes.

Vamos relembrar nossas relações entre as coordenadas esféricas e cartesianas!

x = ρ s i n ϕ c o s θ

y = ρ s i n ϕ s i n θ

z = ρ c o s ϕ

Belezoca! Agora, pensa comigo.

Uma longitude de  90 ° 90 °  oeste corresponde a 

360 ° - 90 ° = 270 ° , ou seja, θ = 270 ° = 3 π 2 r a d

Enquanto  30 ° 30 °  de latitude norte corresponde a 

ϕ = 90 ° - 30 ° = 60 ° = π 3 r a d .

Só para você entender de onde eu tirei isso → a latitude é a coordenada geográfica definida na esfera, então o seu ângulo corresponde a ϕ . Além disso, ela varia de 90 ° em um polo até 0 ° na linha do equador. Já a longitude mostra a localização de um lugar na terra, indo de leste a oeste, ou seja, circundando a Terra. Logo, ela corresponde ao θ .

Assim, as coordenadas esféricas  ( ρ ,   θ ,   ϕ ) ( ρ ,   θ ,   ϕ ) de New Orleans são 

( 4000 , 3 π 2 , π 3 ) ( 4000 , 3 π 2 , π 3 )

Para determinarmos as coordenadas retangulares (cartesianas) , aplicamos as fórmulas de conversão. Assim, obteremos

x = 4000 sin ⁡ π 3 cos ⁡ 3 π 2

x = 4000 . 3 2 . 0 = 0   m i l h a s

y = 4000 sin ⁡ π 3 sin ⁡ 3 π 2

y = 4000 . 3 2 . - 1 = 2000 3   m i l h a s  

z = 4000 cos ⁡ π 3

z = 4000 2 = 2000   m i l h a s

Resposta

x = 0   m i l h a s

y = 2000 3   m i l h a s

z = 2000   m i l h a s