Expressão Analítica de uma TL
Produzido por Bruno PestanaTeoria
Como construir uma ?
Desde que nos entendemos por gente, trabalhamos com funções. A gente aprendeu desde cedo a montar a equação da reta e da parábola a partir de certos valores. Para uma Transformação Linear não é diferente!
Acredito que você já deve ter se perguntado como podemos achar a fórmula dela??? Ou não tenha se perguntado, porque ninguém normal fica se questionando esse tipo de coisa, haha. Mas, enfim, vamos ver um exemplo abaixo:
Seja a transformação dada por:
Como podemos achar a fórmula acima, sabendo apenas que:
Obs: Perceba que sempre temos que receber uma informação antes, para poder montar a nossa .
Passo 1: Veja que os elementos do domínio informados (os que ficam dentro de ), formam uma base para o nosso domínio! Então vamos chamar de uma base do .
Passo 2: Se é uma base de , podemos escrever qualquer vetor do como uma dos vetores dessa base.
Passo 3: Mas nós não queremos achar quem é e sim quem é , pois este nos fornece a fórmula. Então vamos aplicar de ambos os lados:
Como é linear, nós podemos separar essa soma:
E também é possível botar o escalar real para fora.
Passo 4: Ahhh, agora ficou mais fácil! Por sabermos quanto vale e ! Então aplicando as informações do enunciado:
Passo 5: Repare que a fórmula da nossa transformação ainda não está pronta! Precisamos achar quem são e . Para isso, vamos voltar à nossa equação :
Com esta equação podemos achar quanto valem e em função de e . Assim sendo, vamos desenvolver a equação:
Passo 6: Voltando para a equação :
Repare que só conseguimos fazer isso porque tínhamos a imagem dos vetores de uma base do nosso domínio (lembre-se que existe mais de uma base para um conjunto). Ou melhor, a gente sabia quem era aplicado em cada um dos vetores da base do nosso domínio.
Sem essas informações não é possível construir uma !
Resumindo:
- Monte uma base para o seu domínio: os que ficam dentro da
- Faça uma de um vetor genérico do domínio com os vetores da base formada.
- Aplique dos dois lados. E vá usando o fato de ser linear para ir “abrindo” a da base formada, até chegar a termos que você possui informação.
- Use as informações dadas no problema; por exemplo, .
- Ainda falta você escrever as coordenadas do vetor genérico na base escolhida, em função das coordenadas do próprio vetor genérico e substituir na sua .
- Agora você terá a imagem de um vetor genérico em função de vetores que pertencem ao contradomínio, ou seja, a expressão de . :D
Observe que com essas informações, você acha uma única expressão para a sua transformação! Assim, se você tiver uma base para o seu domínio, e aplicado em cada um dos vetores da base, só existe uma única transformação que satisfaz isso!
Obs: Note que a gente não definiu uma base para o contradomínio! Apenas para o domínio!
Exercícios Resolvidos
Exercício Resolvido #1
Lista 3 de Monitoria Álgebra Linear I para a p2, exercício 1-b), 2015.1, PUC-RIO.
Sabendo que
Calcule .
Passo 1
Bom, a primeira coisa a se fazer é verificar se o conjunto dos vetores é .
Podemos ver isso pelo lugar onde os zeros se encontram, e com isso fica fácil de perceber que nenhum dos vetores ou de dois vetores consegue gerar o terceiro.
Tá, mas vamos ao que interessa: começar a montar a nossa !
Passo 2
Vamos fazer uma de um vetor genérico com a base do .
Aplicando dos dois lados:
Devido à ser linear, podemos reescrever a equação como:
Passo 3
Agora vamos aplicar as informações do nosso enunciado!
Substituindo em :
Passo 4
Ainda falta achar quem são em função de .
Passo 5
Agora que achamos os valores que queríamos para , vamos substituir na nossa equação :
Resposta
Exercício Resolvido #2
Lista 1 de Álgebra Linear I para a p2, exercício 9, 2015.1, PUC-RIO.
Encontre uma expressão analítica de uma transformação linear tal que a imagem de seja gerada pelos vetores e . A transformação linear encontrada é a única que satisfaz a condição dada no exercício?
Passo 1
Tá, ele quer uma transformação que vá do para o e que tenha como imagem o espaço gerado por e . Para “criarmos uma ” precisamos da aplicada em uma base do domínio. Mas ele não deu mais nenhuma condição pra gente, então vamos fazer o seguinte:
Agora vamos aplicar a nossa fórmula de bolo:
E pronto, temos uma com a imagem que o enunciado pediu.
Passo 2
Agora que montamos uma expressão para , será que ela é a única possível??
Não!! Fica fácil de ver, se lembrarmos do jeito que construímos a . Veja que tivemos que chutar uma base para o nosso domínio, porém poderíamos ter escolhido outros vetores para a base, que conseguiriam satisfazer as mesmas condições do exercício! Escolhemos esses pra facilitar nossa vida mesmo!
Passo 3
De fato, poderíamos ter respondido à segunda pergunta com o teorema da unicidade da transformação linear, que diz que é preciso ter uma base, e a imagem de cada um dos vetores da base, para a transformação ser única! Se não tiver as condições do teorema, a transformação não é única.
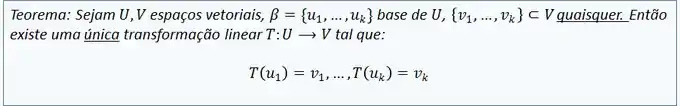
Resposta
Não.
Exercício Resolvido #3
Alfredo Steinbruch e Paulo Winterle, Álgebra Linear, 2ª ed., São Paulo, Pearson, 1987, pp. 214. – 11
Determinar a transformação linear tal que , e .
Passo 1
Bom, temos como base de :
Que claramente é e, além disso, é base canônica de
Então, vamos fazer uma de um polinômio genérico com a base do .
Aplicando dos dois lados:
Devido à ser linear, podemos reescrever a equação como:
Passo 2
Agora vamos aplicar as informações do nosso enunciado!
Substituindo em :
Passo 3
Ainda falta achar quem são em função de .
Passo 4
Agora que achamos os valores que queríamos para , vamos substituir na nossa equação :
Resposta
Exercício Resolvido #4
Como Construir e Inverter Uma TL e Composição de TL's
Existe uma única transformação linear satisfazendo simultaneamente:
- Para todo .
- Os vetores e são transformados por no mesmo vetor de .
Encontre a expressão de .
Passo 1
Vamos estudar algumas informações do enunciado. Repare que:
Assim, ou ou . Como ele está dizendo que aquela afirmação serve para TODO , não vale apenas . E se não vale somente , chegamos a conclusão que:
Isso quer dizer que todos os múltiplos de pertencem ao núcleo, e assim, . Logo,
Passo 2
Outra informação que podemos tirar do enunciado também, é que:
Mas como é linear:
Passo 3
Mas o enunciado também nos diz que os vetores e são transformados por no mesmo vetor de . Então podemos concluir que:
Passo 4
Agora finalmente podemos encontrar a expressão de . Como base para o domínio, vamos utilizar os três vetores que aparecem no enunciado , e .
Como vimos nos passos a :
Logo, aplicando nos dois lados de :
Passo 5
Agora botando em função de :
Substituindo em :
Resposta