Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Teorema Núcleo Imagem

Ver Todos os Exercícios

Teoria

Pra você ter uma ideia da importância desse teorema, ele é conhecido como Teorema Fundamental da Álgebra Linear.

Ta beleza, mas o que esse teorema todo poderoso diz? Bom, ele relaciona as dimensões do núcleo e da imagem com a dimensão do domínio de uma T L . O que ele diz é o seguinte:

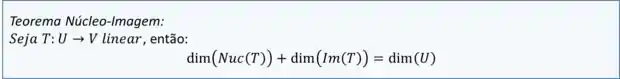
Ou seja, a soma das dimensões do núcleo e da imagem de uma transformação linear é exatamente a dimensão do seu domínio (sim, é igual ao que vimos pra matrizes :p)!

Além de, é claro, facilitar MUITO nosso trabalho pra achar a dimensão do núcleo ou da imagem de uma T L , esse teorema tem implicações muito interessantes.

Por exemplo, lembram daquele macete que eu tinha ensinado pra vocês:

Se as dimensões do domínio e do contra domínio de uma T L são iguais, então temos que ela é injetiva se for sobrejetiva e vice versa. Isso vem do Teorema Núcleo Imagem!

Seja T : V → V linear, então se T é injetiva, temos que dim ⁡ N u c T = 0 . Pelo TNI, temos que dim ⁡ I m T = dim ⁡ V - dim ⁡ N u c T ⏟ 0 = dim ⁡ V . Opa, se a dimensão da imagem é igual à do contra domínio, então ela é sobrejetiva né!

O caminho inverso também é válido, verifica aí ;)

Exercícios Resolvidos

Exercício Resolvido #1

Elaboração Própria

Dada a transformação abaixo:

T x , y , z = ( 2 x , 5 y + z , 4 z )

a ache geradores para o núcleo, e calcule sua dimensão;

b verifique se T é injetiva;

c verifique se T é sobrejetiva.

Passo 1

( a ) Para achar o Núcleo, precisamos achar quais vetores do domínio que aplicados em T levam a transformação em zero. Podemos equacioná-la assim:

T x , y , z = 2 x , 5 y + z , 4 z = 0

Igualando coordenada a coordenada:

2 x = 0 ⇒ x = 0 5 y + z = 0 ⇒ 5 y = 0 ∴ y = 0 4 z = 0 ⇒ z = 0  

Passo 2

Portanto os vetores que geram o núcleo são os vetores que possuem: x = 0 , na primeira coordenada, y = 0 , na segunda coordenada, e z = 0 , na terceira coordenada.

Assim concluímos que:

x , y , z = 0,0 , 0 ∴

N u c T = { 0 }

E, portanto, dim ⁡ N u c T = 0 .

Passo 3

b   Como o Núcleo de T , contém somente o vetor nulo, podemos dizer, pelo teorema que relaciona injetividade e o núcleo, que ela é injetiva.

Passo 4

c Ahh então agora basta calcular os geradores da imagem e sua dimensão e depois... NÃO!!!!!

Até é verdade que podemos fazer isso, se você foi por ai e calculou a dimensão, você está correto! Mas É MUITO MAIS RÁPIDO calcularmos através do teorema núcleo-imagem! Perceba só:

dim ⁡ N u c T + dim ⁡ I m T = dim ⁡ D o m T

Ao olharmos para a fórmula, podemos perceber que a T L “carrega” vetores do R 3 e devolve também no R 3 . Assim:

T : R 3 → R 3

E, assim, dim ⁡ D o m T = 3 .

Passo 5

Aplicando os valores na fórmula temos:

0 + dim ⁡ I m T = 3

Repare que esse 3 é a dimensão do DOMÍNIO! Por acaso, nossa transformação possui domínio e contra-domínio iguais! E, por isso, dim ⁡ C o n t r a D o m T = 3 = d i m ⁡ ( I m T ) .

Como a dimensão da imagem é igual a do CONTRA-DOMÍNIO, a T L é sobrejetiva.

Resposta

a   x , y , z = 0,0 , 0 e N u c T = { 0 } .

b   Sim.

c   Sim.

Exercício Resolvido #2

Marco Cabral e Paulo Goldfeld, Curso de Álgebra Linear Fundamentos e Aplicações, 3ª Ed., Rio de Janeiro, Instituto de Matemática, 2012, pp. 129 – Prob 4.9

Explique em cada caso porque não existe uma T L :

a   T : R 4 → R 2 cujo núcleo seja a origem;

b   T : R 4 → R 2 que seja injetiva;

c   T : R 7 → R 6 com dim ⁡ N u c T = dim ⁡ I m T ;

d   T : R 4 → R 3 com N u c T = 1,0 , 0,0 , 0,1 , 0,0 e I m T = 1,1 , 2 , 2,2 , 4

Passo 1

Pra resolvermos esse exercício temos que ter duas coisas em mente:

A primeira é o TNI:

dim ⁡ N u c T + dim ⁡ I m T = dim ⁡ d o m í n i o

A segunda é que o núcleo e a imagem têm suas dimensões restringidas pelo espaço em que estão contidos. Como assim?

Bom, o núcleo está contido no domínio, logo, sua dimensão será, no máximo, a do domínio.

A imagem, por sua vez, está contida no contra domínio, portanto, sua dimensão será, no máximo, a do contra domínio.

Dito isso, podemos começar.

Passo 2

a Pelo enunciado temos que:

N u c T = 0

Logo,

dim ⁡ N u c T = 0

Aplicando isso no TNI:

dim ⁡ N u c T ⏟ 0 + dim ⁡ I m T = dim ⁡ R 4

dim ⁡ I m T = 4

Opa, temos um problema ai! A imagem de T está contida no R 2 que é o contra domínio. Dessa forma, sua dimensão deve ser no máximo 2 e, portanto, tal transformação não pode existir!

Passo 3

b Se T é injetiva, então:

dim ⁡ N u c T = 0

Logo, pelo TNI:

dim ⁡ N u c T ⏟ 0 + dim ⁡ I m T = dim ⁡ R 4

dim ⁡ I m T = 4

Novamente temos uma imagem de dimensão 4 contida em um espaço de dimensão 2 , o que não é possível!

Passo 4

c Agora temos que dim ⁡ N u c T = dim ⁡ I m T .   Aplicando isso no TNI:

dim ⁡ N u c T ⏟ dim ⁡ I m T + dim ⁡ I m T = dim ⁡ R 7

2 dim ⁡ I m T = 7

dim ⁡ I m T = 3,5

Bom, claramente isso é impossível né. Se você conseguir pensar em um espaço de dimensão 3,5 me conta por favor haha. Última letra gora.

Passo 5

d Nesse caso temos:

N u c T = 1,0 , 0,0 , 0,1 , 0,0

E também que:

I m T = 1,1 , 2 , 2,2 , 4

A dimensão do núcleo claramente é 2 . No entanto, repare que os vetores geradores da imagem são múltiplos um do outro! Logo, a dimensão da imagem é 1 ! Substituindo isso no TNI:

dim ⁡ N u c T + dim ⁡ I m T = dim ⁡ R 4

2 + 1 = 4

3 = 4

Logo, chegamos à conclusão que tal T L não existe.

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #3

Transformações Lineares e Teorema Núcleo-Imagem

Dado v = x 0 y 0 z 0 ∈ M 3 × 1 fixo, a transformação T : M 3 × 3 ⟶ M 3 × 1 dada por T A = A v é linear. Existe algum v tal que T seja injetiva ?

Passo 1

Queremos saber se existe algum v para que T seja injetiva.

Bom, vamos ver se ela é injetiva primeiro. Pelo Teorema Núcleo-Imagem, podemos ver que:

dim ⁡ N u c T + dim ⁡ I m T = dim ⁡ M 3 × 3 ⇒

dim ⁡ N u c T + dim ⁡ I m T = 9

Se ela for injetiva, dim ⁡ N u c T = 0 , e assim, a dim ⁡ I m T = 9 . Só que sabemos que I m T ⊆ M 3 × 1 e, portanto, a dim ⁡ I m T deve ser no máximo 3 (que e é a dimensão do contradomínio). Assim, não existe nenhum v que torne isso possível.

Resposta

Não.

Exercício Resolvido #4

Transformações Lineares e Teorema Núcleo-Imagem

Sejam T   : R n ⟶ R m e S   : R m ⟶ R k duas transformações lineares injetivas. Mostre que n ≤ m ≤ k .

Passo 1

Para mostrar isso, devemos usar o teorema núcleo-imagem. Na transformação T temos:

dim ⁡ N u c T + dim ⁡ I m T = dim ⁡ D o m T

Mas como T é injetiva, dim ⁡ N u c T = 0 e assim:

dim ⁡ I m T = dim ⁡ D o m T = n

Na transformação S :

dim ⁡ N u c S + dim ⁡ I m S = dim ⁡ D o m S

Mas como S é injetiva, dim ⁡ N u c S = 0 e assim:

dim ⁡ I m S = dim ⁡ D o m S = m

Passo 2

-

Agora vamos estudar os casos. Em T sabemos que dim ⁡ I m T = n , e por definição de imagem, ela está contida no contradomínio, R m , então I m T ⊆ R m e assim n ≤ m .

Agora podemos fazer a mesma coisa para a S . Em S , sabemos que dim ⁡ I m S = m e, por definição de imagem, ela está contida no contradomínio, R k , então I m S ⊆ R k e assim m ≤ k .

Logo, podemos concluir que n ≤ m ≤ k .

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #5

Elaboração Própria

Foi perguntado a Vininho se a seguinte proposição é verdadeira:

Se uma transformação linear é injetiva, então ela é sobrejetiva.

E ele respondeu:

“Sim, pois pelo Teorema do Núcleo-Imagem:

dim ⁡ N u c T + d i m ( I m T ) = dim ⁡ D o m T

E como T é injetiva:

dim ⁡ N u c T = 0

Portanto:

d i m ( I m T ) = d i m ⁡ ( D o m T )

Assim, podemos ver que ela é sobrejetiva.”

Qual foi o erro de Vininho? E responda se a proposição é verdadeira ou falsa, e caso seja falsa adicione uma hipótese para que torne a proposição verdadeira.

Passo 1

O erro de Vininho foi não saber a definição de sobrejetividade.

De fato, pelo Teorema Núcleo-Imagem, temos que:

dim ⁡ I m T = dim ⁡ D o m T

A definição de sobrejetividade é que dim ⁡ I m T = dim ⁡ c o n t r a   d o m í n i o E NÃO QUE d i m ⁡ ( I m T ) = d i m ⁡ ( D o m ( T ) ) .

Passo 2

Além disso, podemos concluir que a proposição é falsa. Para torná-la verdadeira deveríamos ter que, além da transformação ser injetiva, a dimensão do domínio da transformação deve ser igual à dimensão do contra domínio, dim ⁡ D o m T = dim ⁡ C D o m T . Ficaria assim:

Se dim ⁡ D o m T = dim ⁡ C D o m T , então a transformação é injetora, se e somente se, é sobrejetora.

Resposta

O erro de Vininho foi não saber a definição de sobrejetividade.