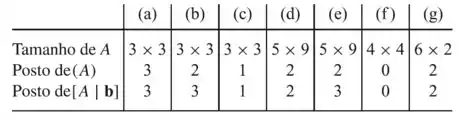
Em cada parte, use a informação na tabela para determinar se o sistema linear é consistente. Se for, dê o número de parâmetros em sua solução geral.

E aí, galerinha, tudo blz? Nesse problema vamos analisar as três informações na tabela e dela retirar as informações pedidas na questão.

Lembrando que um sistema de equações consistente tem pelo menos uma solução, e um sistema inconsistente não tem nenhuma solução. 

(a) Neste item, vemos que os dois postos são iguais. Portanto, o sistema é consistente, com 0 parâmetros ou variáveis livres.

(b) Neste item, os dois postos são diferentes. Portanto, o sistema não é consistente.

(c) Neste item, os dois postos são iguais. Portanto, o sistema é consistente. Para calcular o número de parâmetros basta fazer

Onde é o número de colunas e o posto.

Assim, a solução possui 2 parâmetros ou variáveis livres.

(d) Neste item, os dois postos são iguais. Portanto, o sistema é consistente. Para calcular o número de parâmetros basta fazer

Onde é o número de colunas e o posto.

Assim, a solução possui 7 parâmetros ou variáveis livres.

(e) Neste item, os dois postos são diferentes. Portanto, o sistema não é consistente.

(f) Neste item, os dois postos são iguais, com valor 0. Portanto, o sistema é consistente e possui 4 parâmetros ou variáveis livres.

(g) Neste item, os dois postos são iguais. Portanto, o sistema é consistente, com 0 parâmetros ou variáveis livres.