Enunciado
Álgebra Linear e Geometria Analítica - Um curso de geometria analítica e álgebra linear, Reginaldo J. Santos- Ed: 1º - Capítulo 5.4 - Ex. 4
Determine qual a rotação do plano em que as coordenadas do ponto são
Passo 1
Eaew, tudo em cima contigo?
Resolver esta questão requer que lembremos como fazer uma mudança de sistema de coordenadas em notação de matrizes, temos o seguinte:
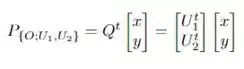
O que nós queremos são os vetores , que são escritos como matrizes colunas! Ou seja, na expressão acima as suas componentes representam as linhas da matriz . No caso específico de uma rotação temos que , tal que:
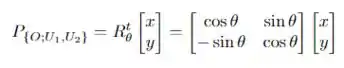
Vamos aplicar agora os valores dados no enunciado. Beleza?
Passo 2
Temos então que:
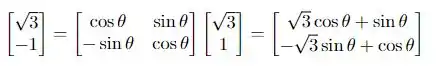
O que nos dá um sistema linear para resolver! Saca só!
Passo 3
Temos a equação:
e
Se obtivermos o cosseno na equação (2) como:
e jogando na equação , temos:
Sendo assim, uma rotação de radianos! A questão é isso, te vejo na próxima! Tchauzinho!
Resposta
Exercícios de Livros Relacionados
Nos Exercícios 17-20, encontre a solução geral do sistema linear e confirme que os vetores linha da matriz de coeficientes são ortogonais aos vetores solução.17. x 1 + x 2 + x 3 = 0 2 x 1 + 2 x 2 + 2
21.(a) A equação x + y + z = 1 pode ser vista como um sistema linear de uma equação em três incógnitas. Expresse uma solução geral dessa equação como uma solução particular somada com uma solução gera
Nos Exercícios 17-20, encontre a solução geral do sistema linear e confirme que os vetores linha da matriz de coeficientes são ortogonais aos vetores solução.18. x 1 + 3 x 2 - 4 x 3 = 0 2 x 1 + 6 x 2
Nos Exercícios 27-28, encontre uma solução geral do sistema e use essa solução para encontrar uma solução geral do sistema homogêneo associado e uma solução particular do sistema dado. 27. 3 4 1 2 6 8
Nos Exercícios 17-20, encontre a solução geral do sistema linear e confirme que os vetores linha da matriz de coeficientes são ortogonais aos vetores solução.20. x 1 + 3 x 2 - 4 x 3 = 0x 1 + 2 x 2 + 3