Enunciado
Álgebra Linear e Geometria Analítica - Um curso de geometria analítica e álgebra linear, Reginaldo J. Santos- Ed: 1º - Capítulo 5.4 - Ex. 3
Sejam
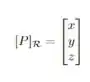
as coordenadas de um ponto em relação ao sistema de coordenadas
e
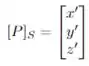
em relação ao sistema de coordenadas . Suponha que temos a seguinte relação:
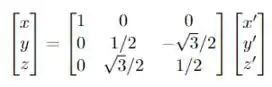
Quais são os vetore e ?
Passo 1
Eaew, tudo em cima contigo?
Resolver esta questão requer entender o que significa ser uma base de um sistema de coordenadas. Os números que temos dentro da matriz do enunciado são relacionados a relação entre um novo sistema de coordenadas e o sistema de coordenadas original. Mas, se analisarmos os vetores de base ortonormal através do próprio sistema, ele se enxergará da forma:
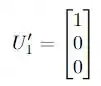
Portanto, podemos utilizar a relação do enunciado para encontrar o formato destes vetores na base canônica do sistema original, que é exatamente a relação dada no enunciado! Saca só!
Passo 2
Se aplicarmos os vetores , temos:
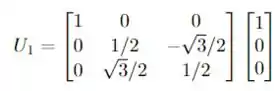
e da mesma forma. para os outros vetores, temos:
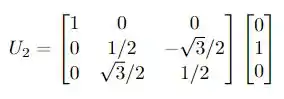
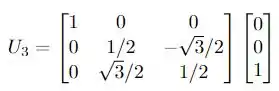
Precisamos calcular os produtos matriciais e temos então o nosso resultado!
Passo 3
Fazendo o produto para cada um dos vetores, temos:
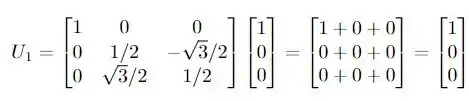
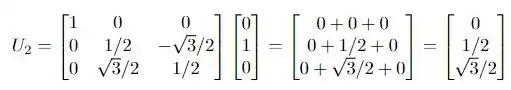
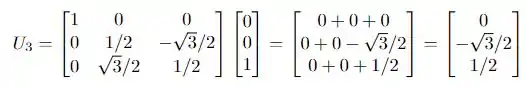
Aí estão nossos três vetores! A questão foi isso, te vejo na próxima!! Tchauzinho!
Resposta
Ao longo dos passos!