Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 8.Elipse - Ex. 1
Esboçar o gráfico e determinar os vértices e , os focos e a excentricidade das elipses dadas.
Passo 1
Faaaala aí! tudo joia?
Vamos começar interpretando essa equação:
Daqui a gente vê que o centro é em , o eixo maior é paralelo ao eixo , e é:
E o eixo menor é:
Continuamos...
Passo 2
Usando a relação:
A gente vai achar :
Pra achar os vértices é só a gente andar unidades em a partir do centro e depois unidades em a partir do centro também...
Passo 3
Então vamos lá... os vértices são:
Os focos a gente anda unidades a partir do centro:
E a excentricidade é só fazer:
Show! Agora com essas informações, a gente vai montar o gráfico😉
Passo 4
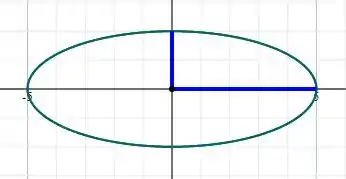
Prontinho😉
Resposta
Vértices:
Focos:
Excentricidade:
Exercícios de Livros Relacionados
Esboçar o gráfico e determinar os vértices A 1 e A 2 , os focos e a excentricidade das elipses dadas. 9 x 2 + 16 y 2 - 144 = 0
Esboçar o gráfico e determinar os vértices A 1 e A 2 , os focos e a excentricidade das elipses dadas. x 2 + 2 y 2 - 5 = 0
Esboçar o gráfico e determinar os vértices A 1 e A 2 , os focos e a excentricidade das elipses dadas. 9 x 2 + 25 y 2 = 25
Esboçar o gráfico e determinar os vértices A 1 e A 2 , os focos e a excentricidade das elipses dadas. 4 x 2 + y 2 = 1
Esboçar o gráfico e determinar os vértices A 1 e A 2 , os focos e a excentricidade das elipses dadas. 4 x 2 + 25 y 2 = 1