Enunciado
Álgebra Linear e Geometria Analítica - Álgebra Linear - 3ª Edição - J. L. Boldrini- Ed: 3º - Capítulo 11.7.2 - Ex. 1f
Esboce o gráfico das cônicas a seguir, determinando seus focos, diretrizes e excentricidade.
Passo 1
Temos uma hipérbole! Como o sinal negativo está em , sabemos que ela não vai tocar o eixo . Vamos começar colocando isso na forma canônica dividindo todo mundo por :
Daí temos e
Passo 2
Esboçando isso, ficamos com:
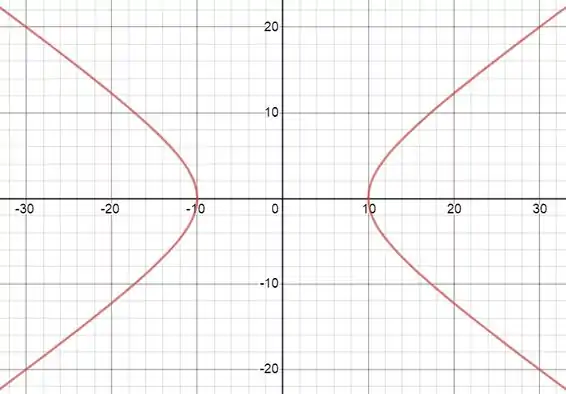
Passo 3
Os seus focos serão dados por: . é dado por:
Sua excentricidade é dada por:
E suas diretrizes serão em:
Resposta
Exercícios de Livros Relacionados
Em cada um dos problemas de 1 a 12 , esboçar o gráfico e determinar os vértices, os focos, a excentricidade e as equações das assíntotas das hipérboles dadas.2. y 2 4 - x 2 9 = 1
Em cada um dos problemas de 1 a 12 , esboçar o gráfico e determinar os vértices, os focos, a excentricidade e as equações das assíntotas das hipérboles dadas.11. x 2 - 9 y 2 = 1
Em cada um dos problemas de 1 a 12 , esboçar o gráfico e determinar os vértices, os focos, a excentricidade e as equações das assíntotas das hipérboles dadas.12. 2 y 2 - 4 x 2 = 1
Em cada um dos problemas de 1 a 12 , esboçar o gráfico e determinar os vértices, os focos, a excentricidade e as equações das assíntotas das hipérboles dadas.6. x 2 - 2 y 2 - 8 = 0
Em cada um dos problemas de 1 a 12 , esboçar o gráfico e determinar os vértices, os focos, a excentricidade e as equações das assíntotas das hipérboles dadas.4. 9 x 2 - 16 y 2 = 144