Enunciado
Álgebra Linear e Geometria Analítica - Vetores e uma iniciacao a geometria analitica mello e watanabe- Ed: 2º - Capítulo 2.Exercícios Propostos - Ex. 2
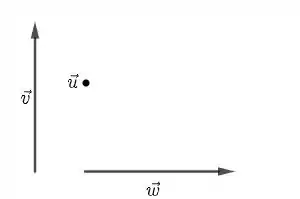
Se possível, desenhe. Se impossível, explique por que.
- l.d., l.i. e l.d.;
- l.d., l.i. e l.i.;
- l.d., l.d. e l.i.;
- l.i., l.i. e l.d..
Passo 1
Mais uma questão, dessa vez temos que analisar várias informações.
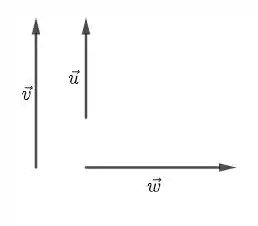
- l.d. indica que um dos vetores é uma combinação linear do outro. l.i. indica que não podemos obter um vetor a partir o outro, ou seja, eles são ortogonais. l.d. indica que deve ser combinação linear de ou os dois. não pode combinação de porque é l.i. Logo, também não pode ser combinação de porque é l.d. Segue que, devem ser paralelos. A figura fica mais ou menos assim:
- A afirmação l.i. é falsa porque l.d.
- l.i. indica que esses dois vetores devem ser ortogonais. l.d., l.d. indica que deve ser paralelo tanto a quanto a , que são ortogonais. A única forma disso ocorrer é se for um ponto.
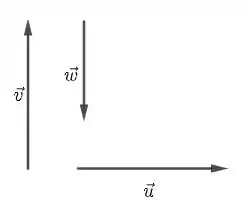
- l.i., l.i. quer dizer que e são ortogonais a . Por outro lado, l.d. indica que não podem ser ortogonais, mas sim paralelos. Assim, temos algo do tipo:
Passo 2
Passo 3
Passo 4
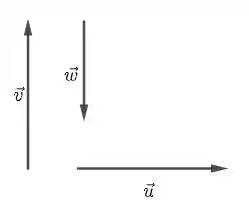
Resposta
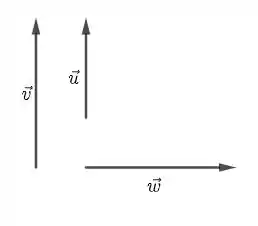
- Impossível
Exercícios de Livros Relacionados
Verifique que a função constante a 3 é combinação linear de g t = 5 t a n 2 t e h t = 2 c o s 2 ( t ) .
Em um triângulo A B C , o ponto M é tal que 3 B M → = 5 M C → . Escreva o vetor A M → em função dos vetores A B → e A C → :
São dados os pontos X e Y . Numa figura, represente estes pontos e mais os seguintes: A tal que A X → = 2 X Y → B tal que X B → = - 1 3 X Y → C tal que C Y → = 4 3 Y X → D tal que Y D → = 2 3 Y X → E
Em um triângulo A B C , o ponto M é tal que 3 B M → = 5 M C → . Escreva o vetor A M → em função dos vetores A B → e A C → :
Os vetores a → ,b → e c → são l . i . Determine uma base de V em relação à qual as coordenadas de a → , b → e c → são, respectivamente, 1,0 , 0 , ( 1,1 , 0 ) e 1,1 , 1 .