Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Vetores e uma iniciacao a geometria analitica mello e watanabe- Ed: 2º - Capítulo 2.Exercícios Propostos - Ex. 1

Observando a figura ao lado, diga se os vetores são l.i. ou l.d. e justifique cada resposta.

  1. b → , c → e y → ;
  2. a → , x → e y → ;
  3. a → , b → , x → e y → ;
  4. a → , w → , com w → =   x →   -   a   → +   b → .

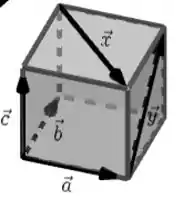
Passo 1

Gente, basicamente o que temos que fazer nessa questãozinha é ver se é possível escrever um dos vetores como combinação linear dos outros. Vamos lá?

  1. b → , c → e y →

    2. Vemos que b → , c → estão num mesmo plano, enquanto y → está num plano paralelo ao plano de b → , c → . Mas, o mais importante aqui é que y → está num plano paralelo ao plano de b → , c → :

    y → =   b → +   c →  

    Então, esses vetores são L.D.

    Passo 2

  2. a → , x → e y →

    3. Nesse caso, a → , x → estão em planos paralelos, então são coplanares. y → está num plano que é ortogonal tanto a a → quanto x → , então não é coplanar com esses dois vetores. Assim, não é possível escrever nenhum dos vetores como combinação linear dos outros dois. Logo, os vetores são L.I.

    Passo 3

  3. a → , b → , x → e y →

    4. Você deve lembrar do conteúdo que quando temos 4 ou mais vetores, eles são sempre L.D. Mas não custa nada ver isso explicitamente. Por exemplo, temos

    x → = a → -   b →

    Passo 3

  4. Como w → =   x →   -   a   → +   b → é uma combinação linear que envolve o vetor   a   → , então a → , w → são L.D.

Resposta

  1. L.D.
  2. L.I.
  3. L.D.
  4. L.D.

Exercícios de Livros Relacionados

Dados os vetores vec u = (3,0 , 1) e vec v = (- 2,1 , 2) , determinar p r o j_vec v vec u e p r o j_u vec v .
Para cada um dos pares de vetores u → e v → , encontrar a projeção ortogonal de v → sobre u → e decompor v → como soma de v → 1 com v → 2 , sendo v → 1 | | u → e v → 2 ⊥ u → . u → = 1,1 , 1 e v → = 3,
Para cada um dos pares de vetores u → e v → , encontrar a projeção ortogonal de v → sobre u → e decompor v → como soma de v → 1 com v → 2 , sendo v → 1 | | u → e v → 2 ⊥ u → . u → = 2,0 , 0 e v → = 3,
Sejam A 2,1 , 3 , B m , 3,5 e C 0,4 , 1 vértices de um triângulo (Figura 2.18 ) responda:Calcular a medida da projeção do cateto A B sobre a hipotenusa B C .
Determinar os vetores projeção de v → = 4 i → - 3 j → + 2 k → sobre os eixos cartesianos x , y e z .