Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 8.Parábola - Ex. 18
Nos problemas de 11 a 26, traçar um esboço do gráfico e obter uma equação que satisfaça as condições dadas.
18) vértice: ; foco:
Passo 1
Neste problema, precisamos construir o gráfico e obter uma equação que satisfaça as condições dadas, certo?
Parece muita coisa, mas é bem tranquilo. Primeiro, vamos encontrar a equação da parábola que respeite as condições dadas e para encerrar, vamos construir o nosso gráfico com o auxílio do software Geogebra. Notem que para o gráfico, precisamos conhecer o vértice, o foco e uma equação diretriz da parábola.
Então, vamos lá?
Passo 2
Antes de colocarmos a mão na massa, precisamos saber se o eixo da parábola é paralelo ao eixo dos ou . Vamos fazer um resuminho.
Sabendo que :
- Se for paralelo ao eixo dos , a equação da parábola na forma padrão é , o foco é dado por e a equação da diretriz é dada por .
- Se for paralelo ao eixo dos , a equação da parábola na forma padrão é , o foco é dado por e a equação da diretriz é dado por .
Notem, que quando for paralelo ao eixo dos , os PRIMEIROS valores do vértice e do foco serão iguais, caso seja paralelo ao eixo dos , os SEGUNDOS valores de e que serão iguais.
Passo 3
Pronto, já sabemos tudo que deveríamos! O bizu é pegar as condições dadas no enunciado e comparar com o nosso resumo, assim matamos a questão rapidinho. Sabemos que , logo:
Já temos os valores de e . Agora, sabendo que foco: , podemos achar o valor de . Não podemos nos esquecer daquele lembrete, como os PRIMEIROS valores e são iguais, o eixo é paralelo ao eixo dos . 😉
Passo 4
Com o valor de em mãos, fica fácil acharmos uma equação diretriz e a equação da parábola.
A equação da diretriz vai ser dada por:
Já a equação da parábola vai ser dada por:
Chegando até aqui, já está certo, mas podemos escrever mais bonitinho...
Passo 5
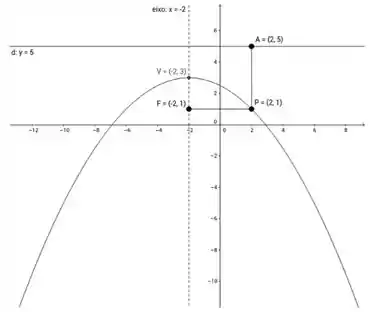
Por fim, com o auxílio do Geogebra, nós construímos o nosso gráfico:
