Prove que se for uma matriz não nula, então e tem valores dominantes positivos.

Se temos , designaremos como , e como

Agora, do ponto de vista geométrico, se temos dois autoespaços e ,e o e decompomos em dois vetores e , logo sempre estará mais perto do autovetor maior!

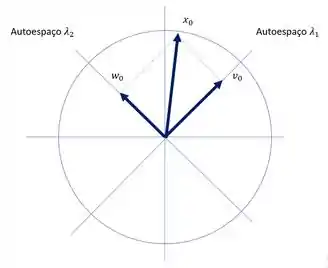
Assim, colocando em uma equação

Portanto, se colocarmos em uma matriz qualquer, temos:

E aplicando para ou para , temos

E se multiplicamos diversas vezes ou e normalizando, temos um vetor que se encontrará um autovalor dominante. Logo:

Assim, o vetor unitário será sempre positivo, implicando que o autovalor dominante também seja, quando aplicado o método das potências. Logo e possuem autovalores dominantes positivos.