Exercícios de Transformação Linear - Lista de Exercícios Resolvida
Questão 1
À questão “Dado fixo, a transformação dada por é linear?”, Andrezinho respondeu da seguinte maneira:
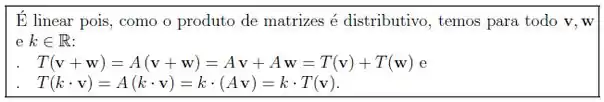
a) Embora seja realmente uma transformação linear, a justificativa do Andrezinho não está correta. Qual foi o erro que ele cometeu?
b) Mostre que é linear.
Ver solução completaQuestão 5
Seja e considere o sistema linear homogêneo
nas incógnitas reais e . Temos que o subespaço de formado pelo conjunto das soluções desse sistema terá dimensão igual a se, e somente se, for igual a:
- ;
- ;
- ;
- ;
- .
Questão 6
01) Seja a transformação linear definida por:
Para quaisquer Considere as seguintes afirmações:
- é injetora;
- é gerado por:
- O subespaço vetorial:
e
De está contido em
Assinale a alternativa correta:
a) apenas a afirmação II é verdadeira;
b) apenas a afirmação I é verdadeira;
c) apenas as afirmações II e III são verdadeiras;
d) apenas a afirmação III é verdadeira;
e) todas as afirmações são verdadeiras.
Ver solução completaQuestão 7
Se é o operador linear que satisfaz , e , e são tais que , então é igual a
Ver solução completaQuestão 8
Seja o operador linear definido por:
Para todos reais. Considere as base de e seja
a base de tal que:
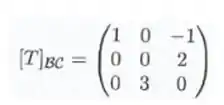
Então é igual á:
Ver solução completaQuestão 9
Considere as bases. , e , bases de ,respectivamente . Se é a transformação linear tal que:
é:
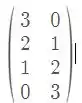
Então
é:
Ver solução completaQuestão 10
Seja um operador linear e considere as seguintes afrmações:
é diagonalizável se, e somente se, a soma das dimensões dos autoespaços de é igual a 16;
se é a matriz que representa com respeito a alguma base de , então
se é diagonalizável e 4, -4, 16, -16 pertencem ao conjunto dos autovalores de , então a matriz que representa com respeito a qualquer base de é inversível.
Assinale a alternativa correta:
apenas as afirmações e são necessariamente verdadeiras;
nenhuma das afirmações é necessariamente verdadeira;
apenas a afirmação é necessariamente verdadeira;
apenas as afirmações e são necessariamente verdadeiras;
apenas as afirmações e são necessariamente verdadeiras.
Ver solução completaQuestão 11
Seja o operador linear definido por:
Para todos reais.
Considere as bases de e seja
a base de tal que:
Então é igual a:
Ver solução completaQuestão 12
Seja um inteiro positivo, um espaço vetorial de dimensão e um operador linear. Considere as seguintes condições:
- É inversível
- Tem autovalores não nulos distintos
- É diagonalizável
Assinale a alternativa correta:
- 1 implica 2; 3 implica 2
- 2 implica 3; 3 implica 1
- 1 implica 2; 3 implica 1
- 2 implica 1; 3 implica 1
- 2 implica 1; 2 implica 3
Questão 13
Seja um operador linear e denote por a matriz que representa com respeito a base canônica de . Suponha que:
;
e
Onde Representa o operador identidade.Então pode ser escrita como:
Ver solução completaQuestão 14
Sejam um inteiro, uma base de , um operador linear e . Denote por o operador identidade de e considere as seguintes opções.
- Se alguma coluna de é combinação linear das outras colunas, então o operador não é sobrejetor.
- Se alguma linha de é combinação linear das outras linhas, então é um autovalor de
- Se tem dimensão , tão não existe um autovalor tal que tenha dimensão
Quais delas são verdadeiras?
Ver solução completaQuestão 15
Seja um espaço vetorial de dimensão e um operador linear cujo polinômio característico é
Denote por o operador identidade de . Então o operador é diagonalizável se e somente se:
Ver solução completaQuestão 16
Sejam F e G os operadores lineares de tais que
Em que B denota a base canônica de e .
Se , então é igual a
Ver solução completaQuestão 17
Decida se cada afirmação abaixo é verdadeira ou falsa. Se a afirmação for verdadeira, apresente uma demonstração. Se a afirmação for falsa, exiba explicitamente um contraexemplo.
a)Se é uma transformação linear, então é base ortonormal de R².
b) Se é uma transformação linear tal que é base ortonormal de R², então T é diagonalizável.
c) Se é uma transformação linear tal que é base ortonormal de R², então T é ortogonalmente diagonalizável.
d) Se é uma transformação linear tal que sua matriz [T] na base canônica é ortogonal , então |det([T])|=1.
Ver solução completaQuestão 18
Considere a função definida por:
(Observe que é a transformação que deriva o polinômio)
Mostre que é uma transformação linear
Ver solução completaQuestão 19
Seja uma transformação linear tal que e . Pode-se afirmar que:
NÃO existe tal transformação linear.
Existem infinitas transformações assim.
Ver solução completaQuestão 20
Considere a matriz
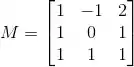
e a transformação linear cuja matriz na base canônica é M.
(b) Determine as coordenadas na base canônica do vetor v que verifica
Ver solução completaQuestão 21
Escolha exatamente três das afirmações abaixo e verifique se cada uma delas é verdadeira ou falsa. Justifique sua resposta.
(a) Seja dada por Então T é uma transformação linear.
Ver solução completaQuestão 22
À questão “Seja a transformação linear definida por e . Encontre a matriz de associada a base canônica de ”, Joãozinho respondeu:

Escreva a definição de transformação linear.
Ver solução completaQuestão 23
Considere a transformação linear dada por
E denote e .
Mostre que para todo , o conjunto é .
Ver solução completaQuestão 24
Seja a transformação linear tal que e . Temos que é igual a:
Escolha uma opção:
Questão 26
Descreva as condições que uma transformação deve satisfazer para ser considerada uma transformação linear.
Verifique se a transformação dada pela fórmula é uma transformação linear.
Ver solução completaQuestão 27
Verifique se é linear a transformação tal que , onde é a matriz transposta de .
Ver solução completaQuestão 28
Seja o espaço vetorial das matrizes quadradas de duas linhas e duas colunas. Para denote sua transposta, ou seja, se , então
Considere a aplicação dada por
(a) Mostre que é uma transformação linear.
Ver solução completaQuestão 29
Seja a matriz uma matriz e
Se é linearmente independente, então é linearmente independente
Se é linearmente independente, então é linearmente independente
a) é falsa e é verdadeira
b) Ambas são falsas
c) é verdadeira e é falsa
d) Ambas são verdadeiras
Ver solução completaQuestão 30
Seja uma transformação linear. Qual das alternativas abaixo é possível?
(a) e
(b) e
(c) e
(d) e
Ver solução completaQuestão 31
Seja o espaço vetorial das matrizes quadradas de duas linhas e duas colunas.
Considere a aplicaçãodada por
a) Mostre que T é uma transformação linear.
Ver solução completaQuestão 32
Assinale a aplicação que NÃO é linear:
, onde é a projeção ortogonal dos vetores do no plano , seguida de rotação de em torno do eixo
, onde
, onde: e é um polinômio de grau .
, onde:
Ver solução completaQuestão 33
Seja a transformação linear definida por
, para toda , em que denota a transposta da matriz . Assinale a alternativa
correta:
(a) é diagonalizável e é um autovalor de com multiplicidade geométrica igual a
(b) é diagonalizável e é um autovalor de com multiplicidade algébrica igual a
(c) é diagonalizável e os autovalores de são e
(d) não é diagonalizável e os autovalores de são e
(e) não é diagonalizável e é um autovalor de com multiplicidade algébrica igual
a
Ver solução completaQuestão 34
Seja a transformação linear tal que
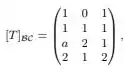
em que denota a base canônica de e denota a base canônica de .Temos que é injetora se, e somente se:
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 35
Seja a transformação linear .
a) Determine bases para e .
b) é um isomorfismo? Justifique.
Ver solução completaQuestão 37
11) Seja a transformação linear tal que:
e
Temos que é igual a:
a)
b)
c)
d)
e) .
Ver solução completaQuestão 38
Seja a transformação linear que realiza uma reflexão em relação ao plano seguida de uma rotação de ângulo no sentido anti-horário em torno do eixo
a) Determine a matriz canônica de
Ver solução completaQuestão 39
A transformação linear leva em e em . Determine não nulo tal que . Essa transformação pode ser sobrejetora?
Ver solução completaQuestão 40
Determine se as afirmações abaixo são verdadeiras ou falsas. Prove as verdadeiras e apresente um contra-exemplo para as falsas.
a) Se é uma transformação linear e é um conjunto linearmente dependente de , então é um conjunto linearmente dependente em
Ver solução completaQuestão 41
Seja a transformação linear que realiza uma reflexão em relação ao plano seguida de uma rotação de ângulo no sentido anti-horário em torno do eixo
b) Utilize a matriz encontrada no item (a), para determinar , onde é um vetor genérico de
Ver solução completaQuestão 42
Q14. Considere as bases e de e de , respectivamente. Se for a transformação linear tal que
Então será igual a:
a)
b)
c)
d)
e)
Ver solução completaQuestão 43
Q10. Seja uma base de e considere a base de dada por:
Se for a transformação linear tal que
Então será igual a:
a)
b)
c)
d)
e)
Ver solução completaQuestão 44
Dê um exemplo, se possível, de uma transformação linear cujo núcleo é o conjunto das matrizes 2x2 simétricas, da forma .
Ver solução completaQuestão 45
Seja T uma transformação linear tal que e . A matriz associada a T é:
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
Questão 46
03) Considere a base de dada por:
e denote por a base canônica de Sejam e as transformações lineares tais que:
e .
Se forem tais que:
Então será igual a:
a)
b)
c)
d)
e)
Ver solução completaQuestão 47
04) Seja a transformação linear definida por
para qualquer Assinale a alternativa correta:
a)
b)
c)
d)
e) é bijetora.
Ver solução completaQuestão 48
Sejam , e A tal que e . Calcule a terceira coluna da matriz A.
(a)
(b)
(c)
(d)
Ver solução completaQuestão 49
Considere o espaço vetorial munido do seu produto interno usual e sejam . Se o operador linear que satisfaz:
for simétrico, então é igual a:
a)
b)
c)
d) ;
e) .
Ver solução completaQuestão 50
Considere as afirmações abaixo
- Se representa uma transformação sobrejetiva, então sempre tem solução para qualquer
- Se é uma transformação linear injetiva e que é gerador de , então é gerador de
- Ambas são falsas
- Ambas são verdadeiras
- Apenas a 2 é verdadeira
- Apenas a 1 é verdadeira
Questão 52
16. Considere as bases e de e seja a transformação linear tal que:
Temos que a soma dos dois autovalores de é igual a:
(a) ;
(b) ;
(c) ;
(d) ;
(e) .
Ver solução completaQuestão 53
01) Seja um espaço vetorial real munido de um produto interno e seja um operador linear simétrico. Se e são vetores de tais que e , então é igual a:
A)
B)
C)
D)
E)
Ver solução completaQuestão 54
Seja a transformação linear definida por
Então,
Escolha uma opção:
- , e uma base de é
- , e a base de é
- , e a base de é
- , e uma base de é
- , e uma base de é
- , e a base de é
- , e a base de é
- , e a base de é
Questão 55
07) Considere a base de dada por
e seja a transformação linear tal que:
Denote por a base canônica de . Se
então e serão iguais respectivamente a:
a) e
b) e ;
c) e
d) e
e) e ;
Ver solução completaQuestão 56
Considere munido do produto interno usual e seja T um operador linear de que satisfaz , para todos . Sejam e suponha que e . Nessa situação, considere as seguintes afirmações:
Está correto o que se afirma em
Ver solução completa
Questão 57
13) Considere a base:
De e a transformação linear tal que
Em que denota a base canônica de . Temos que é igual a:
a)
b) ;
c) ;
d) ;
e) .
Ver solução completaQuestão 58
15) Seja o espaço vetorial de todas as funções e sejam definidas por:
e ,
para qualquer . Temos que:
é uma base do subespaço vetorial de gerado por . Se for a transformação linear definida por:
para qualquer , então será igual a:
a)
b) ;
c)
d)
e)
Ver solução completaQuestão 59
Decida se cada afirmação abaixo é verdadeira ou falsa. Se a afirmação for verdadeira, apresente uma demonstração. Se a afirmativa for falsa, exiba explicitamente um contraexemplo.
e) Se é transformação afim dada por , então para todos os vetores e de .
Ver solução completaQuestão 60
Seja o espaço dos polinômios de grau Sejam base de e base de , e seja uma transformação linear cuja matriz é dada por:
Calcular a transformação linear T(x,y).
Ver solução completaQuestão 61
Identifique se cada afirmação é verdadeira ou falsa. Justifique.
(a) Seja dada por . T é transformação linear.
Ver solução completaQuestão 62
Sejam um espaço vetorial de dimensão 2 e uma transformação linear não nula tal que
Para todo . Considere as seguintes afirmações:
Assinale a alternativa correta:
apenas a afirmação é necessariamente verdadeira;
apenas as afirmações e são necessariamente verdadeiras;
apenas a afirmação é necessariamente verdadeira;
apenas as afirmações e são necessariamente verdadeiras;
apenas as afirmações e são necessariamente verdadeiras;
Ver solução completaQuestão 63
Considere as seguintes afirmações sobre operadores lineares S e T definidos em um mesmo espaço vetorial com produto interno.
Está correto o que se afirma em
Ver solução completa
Questão 65
Seja a transformação linear que satisfaz:
Determine a matriz tal que . A soma de todos os elementos da primeira coluna de vale:
- -2
- -1
- 0
- 1
Questão 67
Seja a transformação linear definida por
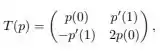
para todo . Temos que
é igual a:
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 68
Seja a transformação linear tal que
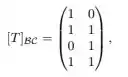
em que B denota a base canônica de e denota a base canônica de . Se são tais que pertence à imagem de , então é igual a:
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 69
Denote por o espaço vetorial de todas as funções contínuas e seja o subespaço de gerado pelas funções:
Seja a transformação linear definida por
, para toda e considere a base de . Temos que a soma das entradas na diagonal principal da matriz é igual a:
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 70
Sejam um espaço vetorial de dimensão bases de a
matriz tal que , para todo . Suponha que
![]()
e sejam as transformações lineares tais que
![]()
Temos que a soma das entradas na diagonal principal da matriz é igual a:
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 71
Considere as seguintes afirmações:
(I) se é uma transformação linear sobrejetora, então
(II) a função definida por
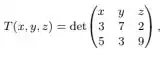
é linear
(III) Se ́e um espaço vetorial de dimensão finita e ́é uma transformação linear, então
Assinale a alternativa correta:
(a) apenas as afirmações (I) e (II) são verdadeiras
(b) todas as afirmações são verdadeiras
(c) apenas as afirmações (I) e (III) são verdadeiras
(d) apenas a afirmação (I) é verdadeira
(e) apenas a afirmação (III) é verdadeira
Ver solução completaQuestão 72
Sejam um espaço vetorial de dimensão e uma transformação linear. Denote por a transformação identidade. Pode-se afirmar que:
(a) se tem dimensão , então é um autovalor de com multiplicidade
geométrica igual a
(b) se é um autovalor de , então a dimensão de é menor ou igual a
(c) tem pelo menos um autovalor
(d) tem no máximo autovalores
(e) se tem dimensão , então é um autovalor de com multiplicidade
algébrica igual a
Ver solução completa