Enunciado
Álgebra Linear e Geometria Analítica - Alfredo Steinbruch e Paulo Winterle - Geometria Analítica- Ed: 1º - Capítulo 8.Problemas Propostos - Ex. 3b
Representar graficamente as seguintes superfícies cilíndricas:
Passo 1
O livro nos diz que o gráfico de uma equação que não contem uma dada variável corresponde a uma superfície cilíndrica cuja equação dada no plano correspondente. Se:
E toca em e toca em .
Então, temos a superfície cilíndrica com geratrizes paralelas ao eixo faltante, e as diretrizes do nosso plano . Então teremos um gráfico com pontos tocando em e e o cilindro cresce em .
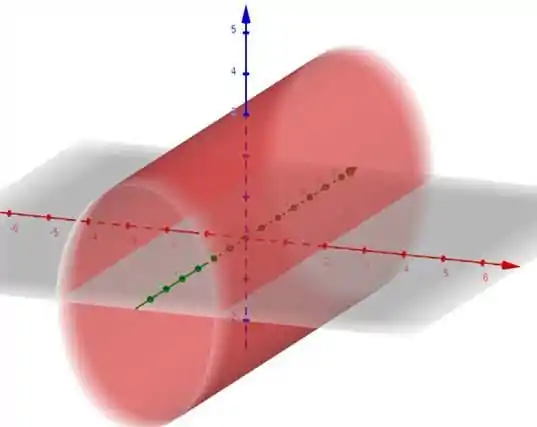
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Identificar e representar graficamente as superfícies expressas pelas equações nos intervalos dados.b) 3 x 2 - y 2 + 2 z 2 , - 6 ≤ z ≤ 6
Identificar e representar graficamente as superfícies expressas pelas equações nos intervalos dados.g) x 2 = 2 z , - 3 ≤ z ≤ 5
Identificar e representar graficamente as superfícies expressas pelas equações nos intervalos dados.h) x 2 - y 2 + z 2 = 0 , - 4 ≤ y ≤ 4
Obter uma equação da superfície gerada pela rotação de cada uma das curvas dadas em torno do eixo indicado: z 2 4 - y 2 = 1 , x = 0 ; e i x oO y
Obter uma equação da superfície gerada pela rotação de cada uma das curvas dadas em torno do eixo indicado: z = 2 y , x = 0 ; e i x oO z