Enunciado

Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 9.Problemas propostos - Ex. 6g

Identificar e representar graficamente as superfícies expressas pelas equações nos intervalos dados.

g)

Passo 1

Neste problema, precisamos identificar e representar graficamente as superfícies expressas pelas equações nos intervalos dados, certo?

Parece muita coisa, mas é bem tranquilo. Primeiro, vamos identificar a superfície quádrica e para encerrar, construiremos o nosso gráfico com o auxílio do software Geogebra, notem que no problema 6, temos intervalos!

Putz... mas eu não sei aonde eu vou usar esses intervalos.

É moleza, eles só vão delimitar o nosso gráfico. 😉

Então, vamos lá?

Passo 2

Antes de colocarmos a mão na massa... PARA TUDO! SE VOCÊ JÁ SABE TUDO SOBRE SUPERFÍCIES QUÁDRICAS, PODE PULAR PARA O PASSO 3, AGORA SE VOCÊ QUISER DAR UMA LEVE RELEMBRADA, VEM COMIGO.

Vamos fazer um resuminho das nossas “temidas” superfícies quádricas, beleza? Mas, como são essas quádricas?? Como definimos??

Relaxa aí!! Vamos te explicar tudinho. 😉

Para analisar todos os tipos de quádricas, devemos partir da equação geral das quádricas que é:

Para termos uma quádrica, um dos coeficientes ou devem ser diferentes de zero.

Assim, resumiremos numa tabela, a seguir, algumas quádricas especiais que são subconjuntos da expressão acima.

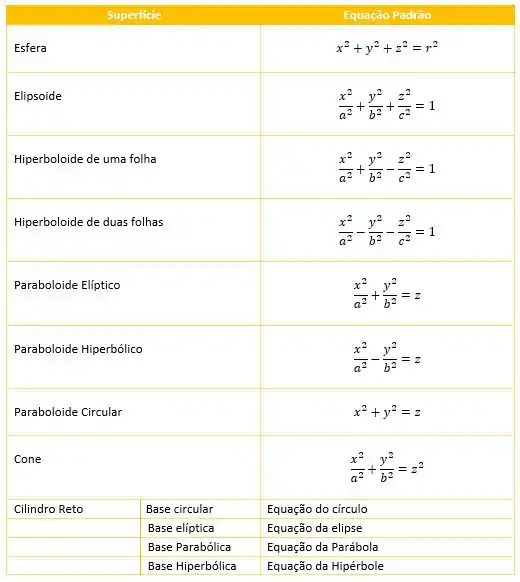
Show!!! Viram como elas não são tão “temidas”.

Passo 3

Pronto, já sabemos tudo que deveríamos. Agora vamos praticar! O bizu para encontrar qual é a superfície apresentada, é reescrever a equação dada no enunciado, de modo que ela se assemelhe a uma das equações da nossa tabela:

Como podemos notar, essa equação não precisa ser simplificada ou reescrita, pois já se encontra num modelo que se assemelha à equação de uma superfície cilíndrica parabólica. 😉

Passo 4

Logo, a equação dada é a que representa uma superfície cilíndrica parabólica e, no intervalo dado seu gráfico é:

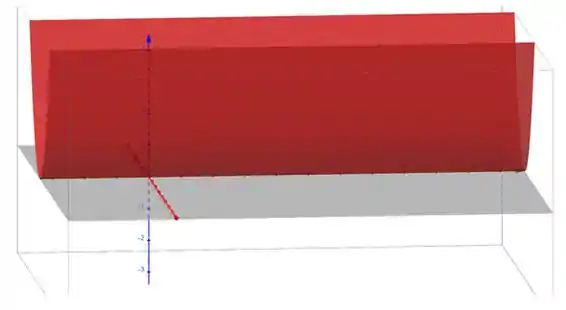
Resposta

Superfície cilíndrica parabólica

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Obtenha uma equação da superfície gerada pela rotação de Γ = Ω 1 ∩ Ω 2 em torno de O z .(b) Ω 1 : y = 0 Ω 2 : 3 x 2 + 3 z = 1

Obtenha, em cada caso, uma da superfície gerada pela rotação da curva Γ = Ω 1 ∩ Ω 2 em torno de O x (no item (c), e é o número de Euler).(e) Ω 1 : y = 0 Ω 2 : ( x - 2 ) 2 + z - 1 2 = 1

Obtenha uma equação da superfície gerada pela rotação de Γ = Ω 1 ∩ Ω 2 em torno de O z .(a) Ω 1 : y = 0 Ω 2 : x 2 + z 2 = 1

Obtenha, em cada caso, uma da superfície gerada pela rotação da curva Γ = Ω 1 ∩ Ω 2 em torno de O x (no item (c), e é o número de Euler).(f) Ω 1 : y = 0 Ω 2 : x = 2

Obtenha, em cada caso, uma equação livre de parâmetros para a superfície gerada pela rotação da curva Γ em torno de O z ( Γ é descrita por equações paramétricas).(a) Γ : x = λ ,y = λ 2 ,z = λ 2 λ ∈ R