Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 1.O tratamento algébrico - Ex. 14b
Sendo e extremidades de um segmento, determinar:
- os pontos e que dividem o segmento de em três partes de mesmo comprimento.
Passo 1
- Primeiro vamos ver graficamente esses pontos para analisar melhor:
Se os pontos e que dividem o segmento de em três partes de mesmo comprimento podemos ter a igualdade para o ponto :
Para achar temos que os segmentos deve ser igual a , vamos então achar o ponto :
Pronto, temos então o ponto .
Agora vamos fazer a comparação para o outro ponto, igualando os dois segmentos correspondentes a cada situação.
Passo 2
Vamos analisar os pontos que temos até agora no gráfico para ver como vamos achar o ponto :
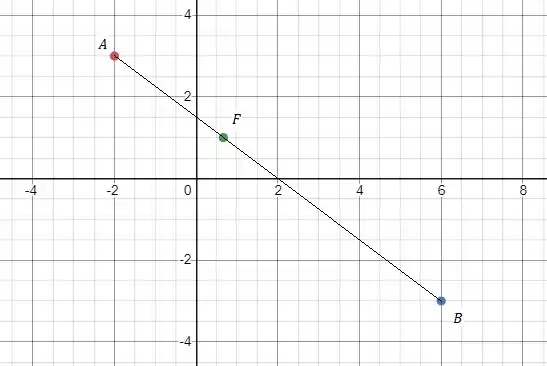
Como os pontos e que dividem o segmento de em três partes de mesmo comprimento, podemos achar fazendo com que o segmento seja igual a , vamos então achar o ponto :
Pronto, temos então o ponto .
Vamos ver todos os pontos juntos:
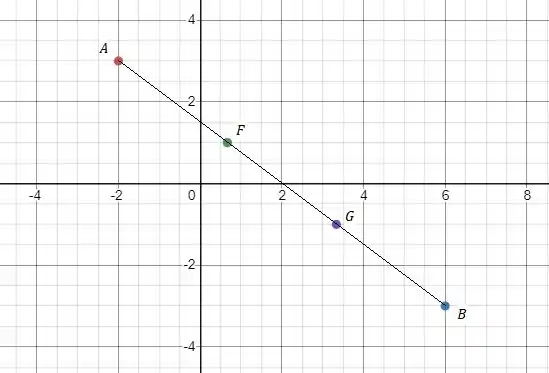
Resposta
e
Exercícios de Livros Relacionados
8) Dados os veotres u → e v → da figura 1.32, mostrar, em um gráfico, um representante do vetor x → = u → - v →
8) Dados os veotres u → e v → da figura 1.32, mostrar, em um gráfico, um representante do vetorc) x → = - v → - 2 u →
8) Dados os veotres u → e v → da figura 1.32, mostrar, em um gráfico, um representante do vetord) x → = 2 u → - 3 v →
No triângulo ABC (Figura 1.33) seja A B → = a → e A C → = b → . Construir um representante de cada um dos vetoresb) a → - b → 2
No triângulo ABC (Figura 1.33) seja A B → = a → e A C → = b → . Construir um representante de cada um dos vetoresa) a → + b → 2